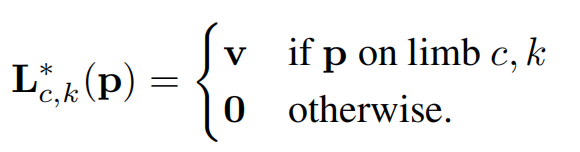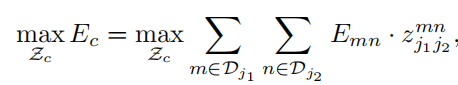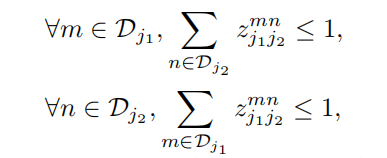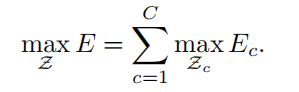摘要

  我们提出了一个方法，能够在一张图中高效的识别出多人的2D姿态。该方法运用了非参数表示（non-parametric representation），我们称之为部分亲和域（PAFs：Part Affinitu Fields）,用它来学习怎样将身体部分和个体联系起来。这个结构编码了全局信息，并允许一个贪婪的从底向上的解析步骤，这在实现实时性能时，有着高度的精准且无须考虑图像中人的数量。这个结构被设计成相同顺序预测过程的两个分支，来联合学习部分位置（关节点）以及它们之间的关联（相邻的关节点的连接关系）。我们的方法在the inaugural COCO 2016 keypoints challenge中首次提出，并且在性能和有效性上，都超过了之前在MPII Multi-Person基准上的最佳方法
 

论文中的个别词，刚开始直接翻译，理解略微不顺。所以后面直接使用它指代的含义进行翻译。如：
part，指的是关键点集，
part locations：关键点的定位
part affinities：关键点之间的亲和度，也就是连接关系。

1. Introduction

  人体的2D姿态估计，在定位人体的关键点或者部分关键点，主要集中在寻找个体的身体部位（表述不清晰）。在图中预测多人的姿态，尤其是社会性的个体（各种状况的姿势）面临着独特的挑战。首先，每张图片中的人体数量是未知的，并且这些人存在不同位置和不同大小。第二，人与人之间的交互产生复杂的空间推理，比如，接触、遮挡、肢体关节等因素是各部分之间的联系变得困难。第三，运行时间复杂度会随着图片中的人的数量而增大，从而实时性能是一个挑战。
   常见的方式是利用人体检测器检测出所有人体，然后进行单人的姿态估计。这种自上而下的方法直接利用已有的技术来做单人姿态估计，但是容易出现的问题：如果人体检测器失败了（当人体靠近时容易发生），那么检测结果是无法恢复正确的。进一步说，自上而下方法的运行时间与人体数量成正比：每一个人体，都要运行一次单人姿态估计，如果图片中存在很多人，那么就需要花费大量时间。与之相反，自下而上是吸引人的，因为它们提供了早期结果的鲁棒性，并且具有潜在的能力来解耦图片中人体的数量和运行时间复杂性的关系。并且，自下而上的方法不直接使用来自另外身体部分和另外的人体的全局信息。实际上，自下而上的方法不能保证效率的提高，因为最后的解析需要花费高昂的全局推理。例如，Pishchulin等人提出开创性的研究，提出了一个自下而上的方法，可以标记出候选检测内容（关键点）以及它们与个体的联系。但是，在一个全连接图上解决整数线性规划问题是一个NP-hard问题，而且处理这类问题需要几个小时。Insafutdinov等人建立了基于ResNet的部分检测器和图像的从属成对分数（image-dependent pairwise scores）的模型。很大的提高了运行时间，但这个方法处理每张图片然然需要几分钟，因为受限于部分提议的数量（指的是图中人体的个数）。在论文[11]中使用成对表现（pairwise representations），很难做精确的回归，因此需要独立的逻辑回归。
 

non-deterministic polynomial：非确定性多项式，NP-hard问题通俗的来说是其解的正确性能够被很容易检测的问题，“很容易检测”值的是存在一个多项式检测算法

  在这篇论文，我们提出了一个多人姿态评估有效的方法，其准确性在多个公共标准达到了领先水平。我们第一个提出利用部分亲和域（PAFs：Part Affinitu Fields）来表示自上而下的联系分数，PAFs，是图片中2D向量集，编码了肢体的定位和方向。我们证明了同时推断自下而上的 【检测 (应该指关键点) 和联系 (应该指部分亲和域，也就是关节点之间的连接关系) 】,对全局上下问进行了足够好的编码，来允许贪婪的解析获得高质量的结果，而花费的计算成本只是一小部分。（这句话顺了老半天，把英文的断句附上）。我们已经开源了代码，能够完整的复现，并正式发布了这史上第一个实时多人姿态检测系统。

We demonstrate that 【【simultaneously inferring these （bottom-up representations of detection and association）】 encode global context sufficiently well to （allow a greedy parse to achieve high-quality results）】, at a fraction of the computational cost.

2. Method

   图2展示了我们的方法的整体流程。将一张大小为$w\ast h$彩色图作为输入(图2a)，将带有每个人体的关键点信息作为输出(图2e)。首先，一个前馈神经网络，同时预测人体关键点的置信图集S(图2b)，以及关键点的亲和度的2D向量域集L(图2c),这编码了各个关键点之间的关联度。
集合$S=(S_1,S_2,...,S_j)$共有$J$个置信度，每个部位一个，其中 S ∈ R w ∗ h , j ∈ { 1... J } S\in R^{w*h},j\in \{1...J\} S∈Rw∗h,j∈{1...J}。
集合 L = { L 1 , L 2 , . . . L C } L=\{L_1,L_2,...L_C\} L={L1​,L2​,...LC​}共有$C$个向量域，其中 L C ∈ R w ∗ h ∗ 2 , c ∈ { 1... C } L_C \in R^{w*h*2},c \in \{1...C\} LC​∈Rw∗h∗2,c∈{1...C}。每一个图片在定位$L_c$处编码一个2D的向量。最后，置信度图和亲和域通过贪心推断算法来解析(图2d)，来得到图片中的每个人的2D关键点

2.1. Simultaneous Detection and Association

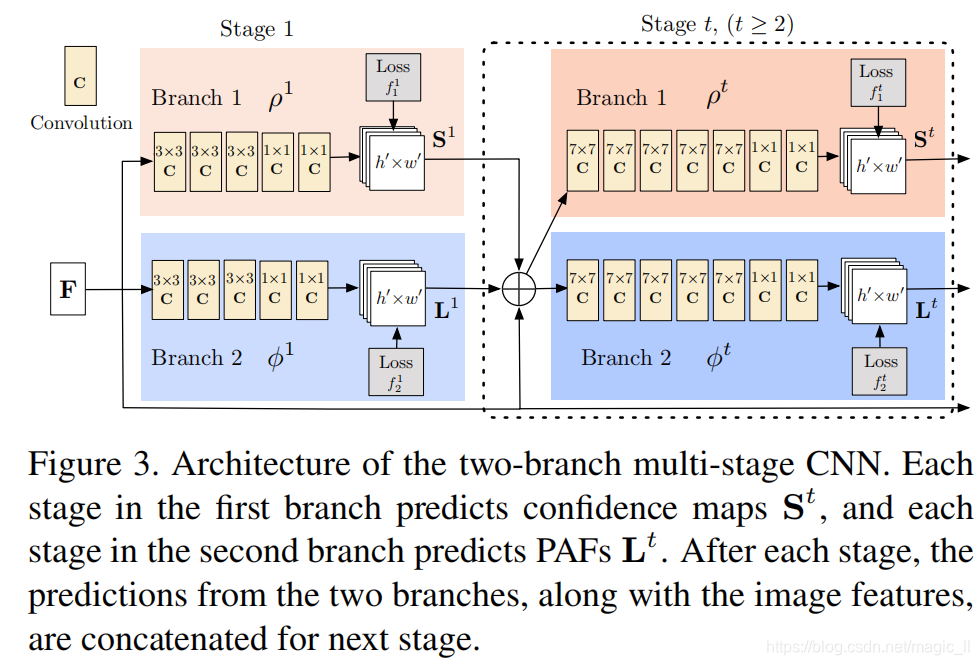
   我们的结构，如图3所示，同时预测置信图和编码了部分到部分联系的亲和域。网络结构分为两个分支：上分支：预测关键点的热量图；下分支：预测亲和域。每一个分支都是一个迭代的预测结构。（如同引用的第31篇论文的S.-E. Wei等人所采用的方式），这种连续重复的阶段优化了预测结果，每个阶段都会有中继监督。
图像首先通过卷积网络进行分析（使用VGG-19的前10层来初始化并且微调），生成了一组特征图F，作为stage1的输入。在第一阶段，网络产生一组关键点置信度图$S^1={\rho }^1(F)$，一组亲和域$L^1={\varphi }^1(F)$，这里的 ${\rho }^1,{\varphi }^1$是stage1的预测的网络结构。在后续的stage中，前一个的两个分支预测和原始图像特征F，进行拼接合并（concat），用于产生更好的预测结果。$$S^t={\rho }^t(F,S^{t-1},L^{t-1}),\forall t\ge 2$$ $$L^t={\varphi }^t(F,S^{t-1},L^{t-1}),\forall t\ge 2$$

图4展示了置信度图和亲和域在不同阶段优化的结果。为了引导网络结构反复预测置信度图和亲和域，我们在每个stage后都使用了损失函数。我们对预测结果和真实标签使用了L2损失。我们对损失函数使用了空间加权，来解决一些数据并不是由所有人的标签的问题。特别的stageT的两个分支的损失函数为：$$f_S^t=\sum _{j=1}^{J}w(p)\ast ||S_j^t(p)-S_j^{\ast }(p)|{|}_2^2$$ $$f_L^t=\sum _{c=1}^{C}w(p)\ast ||L_c^t(p)-L_c^{\ast }(p)|{|}_2^2$$其中，$S_j^{\ast }$为真实的关节点置信图，$L_c^{\ast }$为亲和向量域。$W$是二值掩码，当$W(p)=0$表示关键点P的实际标注丢失。这个掩码用于避免在训练时惩罚（降低）真实积极的预测。**在每个stage后进行中继监督，通过周期性的补充梯度，解决了梯度消失的问题。**总的损失为$$f=\sum _{t=1}^T(f_S^t+f_L^t)$$

2.2 Confifidence Maps for Part Detection

   为了评估训练阶段中的$f_s$，我们从标注的2D关节点生成真实置信度$S^{\ast }$。每一个置信图是2D表示的，在每个像素出现的可信度。理想情况下，如果图像中只有一个人，并且这个人的关键点都可见，那么就在每张置信图中存在一个单峰值；如果出个人出现，那么对于每个人的可被看见的第 j 个关节点都会有相应的峰。
我们为每个人生成置信图$S_{j,k}^{\ast }$。$x_{j,k}\in R^2$是图中第k个人的第 j 个关键点的真实位置，那么对于$S_{j,k}^{\ast }$来说，在位置$p\in R^2$的值定义为$$S_{j,k}^{\ast }(p)=exp(-\frac{||p-x_{j,k}|{|}_2^2}{{\sigma }^2})$$其中 $\sigma$ 是控制着峰的范围。通过网络被预测的真实置信图，是个体置信度经过一个max
operator后的聚合体。$$S_J^{\ast }(p)=\underset{k}{\max }{S}_{j,k}^{\ast }(p)$$如图所示，我们使用置信图的最大值而不是平均值，这样可以让两个邻近的峰的精度保持不同。在测试的时候，我们预测置信图，并且通过非极大值抑制来获取候选人体关键点
 

这里有意思了，主要说的是训练时，将标注的2D关键点转化到置信图的过程。以及测试时，将神经网络输出的置信图转化成2D关键点的过程。
【2D keypoint --> confidence maps】

• 我们需要先明确，无论图像中存在多少人(每个人有j个关键点)。该图像的每种关键点都只会产生一张置信图，包含着每个人的该关键点的信息。
• 第 j 个关键点可以生成一张置信图。生成的方式是二阶高斯函数，也就是该节内容的第一个公式。单个人关键点效果图为当存在 k 个人时，会存在 k 个峰。最终该张置信图每个像素的数值，是对 k 个峰求max。
  

2.3 Part Affifinity Fields for Part Association

  给出一组检测出的部分人体关键点（如图5），当我们不知道有多少人时，我们如何组合这些关键点来形成完成的人的姿态？我们需要人体检测出的相邻关键点之间联系的置信测量，即 这些关键点是否属于同一个人。一种可行的衡量关联的方式是检测额外的中间点，中间点处于每个肢体的两个关键点之间。
然而，当人们聚集在一起时，这些中间点可能支持错误的连接方式。这种错误的连接的出现是因为两种限制：（1）它只编码了每个肢体关键点的位置，没有编码肢体方向，（2）它减少了肢体对于一个单点的支持区域（应该是说，当(一对肢体点中)只有一个点出现时，那么这个肢体就缺失了连接）
 

图4
关键点关联策略：

• (a) 检测出身体某一对的关键点对的所有候选点，如上图(a)中的红色点集、蓝色点集，以及两个点集之间所有可能的连线（灰色）
• (b) 使用中点(黄色点)表示的连接结果：黑色的正确的连接、绿色的错误链接都满足这个约束
• (c ) 使用 PAFs 的连接结果
   

通过编码关键点的位置信合和连接信息，PAFs 可以排除了错误的连接。

---

  为了解决这些限制，我们提出一个叫做 part affifinity fifields 的新奇的特征表示，它保存着关键点位置和方向的信息。部分亲和是每一个肢体的2D向量：对于属于每个肢体区域的每个像素，2D向量编码了肢体的一端点到另一端点的方向。每个肢体都有对应的亲和域来将肢体两端的关键点联结起来。
只考虑只有一个肢体时，如下图所示。

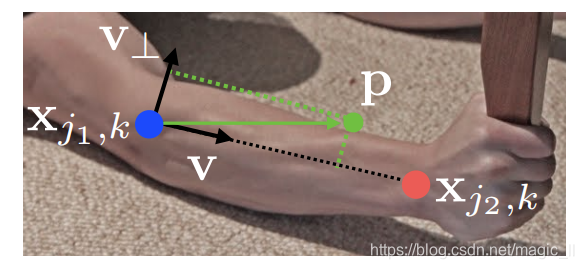
设图中 $X_{j1,k}$ 和 $X_{j2,k}$ 是第 k 个人的肢体 c的两端关键点$j_1,j_2$ 的真实位置。图中已知关键点$j_1,j_2$ 的单位方向向量 $v$、任意一点 p ，当它在手臂上时，$L_{c,k}^{\ast }(p)$ （也就是p位置的像素）的值是 $v$，当它不在手臂上，像素值为0。
在训练时计算总损失函数，我们定义了真实亲和域，$L_{c,k}^{\ast }$ 在图中任意点p的值为

• 这里关键点$j_1,j_2$ 的单位方向向量 $v$： $v=(X_{j2,k}-X_{j1,k})/||X_{j2,k}-X_{j1,k}|{|}_2$
• 在肢体上的点集的定义为：在一定距离阈值之内的点集，即满足以下条件的点p：$0\le v\cdot (p-X_{j1,k})\le l_{c,k}$ and  $|v_{\perp }\cdot (p-X_{j1,k})\le {\sigma }_l$ 其中肢体宽度 ${\sigma }_l$是像素上的距离，
• 肢体长度 $l_{c,k}=||X_{j2,k}-X_{j1,k}|{|}_2$，
• $v_{\perp }$ 是 $v$的垂直向量。
   

真实部分亲和域是图片中所有人的肢体c的平均值$$L_c^{\ast }(p)=\frac{1}{n_c(p)}\sum _k{l}_{c,k}^{\ast }(p)$$其中$N_c(p)$是所有 k 个人在点 p 处的非零向量的数目（即不同人的肢体重叠处的像素平均值）

---

   在测试中，我们通过对应的PAF，来计算 连接候选点的线段上的线积分，然后获取候选点之间的连接。换句话说，我们计算预测的PAF与候选肢体的alignment（这里应该指“距离”/"差距"等意思），其中候选肢体将检测到的身体关节点连接而成。具体来说，对于两个候选位置 $d_{j1}/d_{j2}$，我们沿着线段与预测的亲和域 $L_c$ 进行采样，测量它们之间的关联的置信度。$$E={\int }_{u=0}^{u=1}{L}_c(p(u))\cdot \frac{d_{j2}-d_{j1}}{||d_{j2}-d_{j1}|{|}_2}du$$ 这里$p(u)$ 是肢体两端关键点$d_{j1},d_{j2}$ 的之间的点集（两个关键点之间的插值点）。$$p(u)=(1-u)d_{j1}+u{d}_{j2}$$实际中，我们通过取样u的等间距值，求和对应L值来计算积分。

• $L_c(p(u))$ 是在点p位置上的PAF数值；
• $\frac{d_{j2}-d_{j1}}{||d_{j2}-d_{j1}|{|}_2}$ 是两个关键点之间的单位向量
• $p(u)$ 是两个关键点之间的插值
• $E$ 是通过计算PAF L 和向量$d_{ij}$之间的点积得到的。
   

例如计算关键点之间连线的10个插值点，然后这10个插值点的PAF与单位向量$d_{ij}$ 之间的点积。如果这些插值点的70%都满足判断标准，则该关键点对是有效的

2.4 Multi-Person Parsing using PAFs

我们在检测出的置信图上使用 非极大值抑制 来获取候选关键点的离散集。对于每个关键点，我们可以由几个候选点，这是由于图片中存在多人或者错误预测情况，如图下图中 (b)。这些候选关键点定义了一个有可能为肢体的大的集合。我们用在PAF上线积分计算的结果来给每个候选肢体打分（如前面讲解的 $E$）。找出最优划分的问题，是一个k维匹配问题，即一个NP-Hard问题。

NP-Hard问题【non-deterministic polynomial，非确定性多项式，NP-hard 问题通俗来说是其解的正确性能够被“很容易检查”的问题，这里“很容易检查”指的是存在一个多项式检查算法（摘自百度）】

在这篇论文中，我们提出了一个贪婪松弛，它可以不断的产生更准确的匹配。我们猜测原因，由于PAF网络更大的感受野，成对关联的得分隐式的编码了全局上下文。
正式的，我们首先获取图中多人的人体检测的候选关键点 $D_J$ ，

• D J = { d j m : f o r   j ∈ { 1... J } , m ∈ { 1... N j } } D_{J}= \{ d_j^m: for \ j\in \{1...J\},m\in \{1...N_j\}\} DJ​={djm​:for j∈{1...J},m∈{1...Nj​}},
• $N_j$ 是关键点 $j$ 的候选数量，
• $d_j^m\in R^2$ 是关键点 $j$ 的第 $m$ 个检测候选位置。
   

这些检测的关键点的候选点依然需要与同一个人的其他关键点进行连接。换句话说，我们需要找出正确的每对的肢体连接。我们定义变量 z j 1 j 2 m n ∈ { 0 , 1 } z_{j_1j_2}^{mn} \in \{0,1\} zj1​j2​mn​∈{0,1} 表示两个相连的关键点 $d_{j1}^m$ 和 $d_{j2}^m$ 是否相连，目标是为了找到 所有正确连接的集合的最优分配。其中

• Z = { z j 1 j 2 m n ∈ { 0 , 1 } : f o r   j 1 , J 2 ∈ { 1... J } , m ∈ { 1... N j 1 } , n ∈ { 1... N j 2 } } Z= \{ z_{j_1j_2}^{mn} \in \{0,1\}: for \ j_1,J_2 \in \{1...J\},m\in \{1...N_j1\},n\in \{1...N_j2\}\} Z={zj1​j2​mn​∈{0,1}:for j1​,J2​∈{1...J},m∈{1...Nj​1},n∈{1...Nj​2}},
   

如果我们考虑一对关键点$j_1,j_2$（代表着第 c 个肢体），那么找到最优相关 将简化成一个最大权重二分图匹配问题。例子图下图(b)所示。在这个图匹配问题中，图的节点是检测的身体关键点的候选点 $D_{j1},D_{j2}$，它的边是检测点之间所有可能的成对连接方式。另外，每一个边的权重由公式求 $E$ 来确定，即关键点的亲和的总和。二分图的匹配是 通过两边没有共享一个节点的方式，来选出边的子集。我们的目标是在边中找到一个有最大权重的匹配，

• $E_c$是c类肢体的的匹配的总体权重，
• $Z_c$是 c类肢体的 Z的子集，
• $E_{mn}$是关节点 $d_{j1}^m、d_{j2}^n$之间的亲和度 （前面公式定义的 $E$）
   

上图后面两个公式，确保没有两个边共享一个节点，没有两个相同类型的肢体共享一个关节点。我们可以使用 Hungarian算法【引用论文14中的算法】来获取最优的匹配。
 
当需要找到多个人完整的姿态时，确定 $Z$ 是一个 k 维的匹配问题。这是一个 NP Hard问题，同时存在很多【松弛】（应该是找寻最短路径问题。链接1 、链接2）。
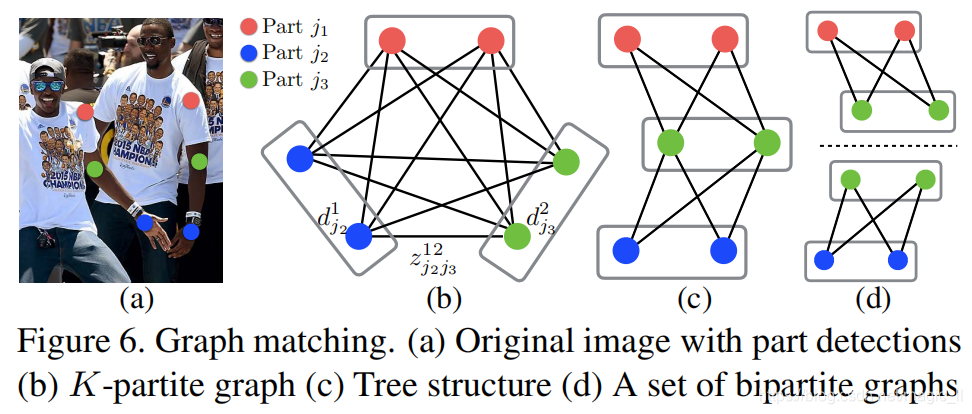
这项工作中，我们在我们的范畴里，添加了两个松弛算法到优化里。首先，我们选择一个最小边数来获取人体姿势的一块棵生成树的骨架，而不是使用完成的图，如图 (c )。然后，我们进一步的将这个匹配问题分解成二分图匹配的集合，同时分别确定【相邻树节点】的匹配，如图 (d)。我们在3.1节中展示了结果对比，证明了最小贪心推断 可以在很小的计算成本上得到很好的全局结果。原因是在相邻树节点时间的关系可以通过PAFs精准的模型化，但内在的，不相邻节点之间的关系通过CNN隐式的模型化了。这一性质的出现是因为CNN训练时有个很大的感受野，同时不同相邻树节点的PAFs 也会影响着预测的PAF。

这两个【松弛】，优化式被简单的分解为

因此对于每种肢体类型，我们使用本节内容的前三个公式，分别获取了每个肢体连接的候选。对于所有肢体连接的候选，我们组合这些共享同一个关键点的连接，来得到多人完整的姿势。我们的基于数结构的优化方案是数量级的快于基于全部连接图上的优化。

3. Result

我们评估我们的方法在两个多人姿态估计的基准上完成：（1）MPII 人体多人姿态估计、（2）COCO 2016 关键点挑战数据。这两个数据集收集了不同场景下的图片，其包含许多真实世界的挑战，例如：拥挤的人群、不同尺寸、遮挡、接触。我们的方法创造了先进的效果在开始的COCO数据集上，而且明显的超过之前在MPII数据集上的最先进的效果。我们还提供了运行时间来量化系统的效率。下图展示了我们算法的一些定性结果。

3.1 Results on the MPII Multi-Person Dataset

为了对比MPII数据集，我们使用工具包来测量 基于PCKh阈值的人体关键点的mAP(mean Average Precision)。表1 在相同的288个测试图片上，使用我们的方法和其它方法对比了mAP 性能，另外在整个MPI测试集，还有我们自己的验证集上的自我比较。除了这些测量，我们在每张图上比较了平均 预测/优化 时间。对于288子测试集，我们的方法比之前最先进的自下而上的方法好了8.5%的mAP。惊人的是，我们的预测时间少了6个数量级。我们在3.3节中报告了更详细的运行时间分析。对于整个MPII数据集，我们的方法不用尺度搜索已经比之前最先进的方法要好很多，即在mAP上了13%。使用了3个尺度(x0.7, x1, x1.3)进一步的增加性能，mAP提高到75.6%。与之前的自下而上的方法的mAP相比较，表明了我们新的特征表示的有效性。基于树结构，我们的贪心划分方法，与基于全部连接图的图割优化公式相比，实现了更好的准确性。
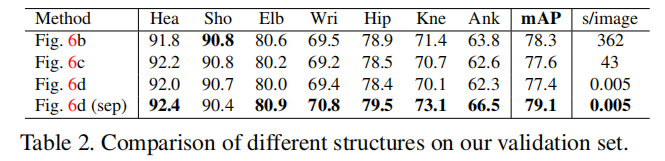
在表2中，我们我们展示了在我们验证集中，使用图6中不同结构的对比结果，343张不在MPII训练集中的图片。我们基于全连接图训练我们的模型，并与选择所有的边的方式进行对比（图6b，用整数线性规划近似求解），以及最小树边（图6c，用整数线性规划近似求解。以及图本文算法图6d，使用贪心算法）。他们相似的性能表示了使用最小表就足够了。我们训练另外一个模型，只学习最小欧变来充分利用网络容量，正如这篇论文所展示的方法图6d。这种方式保持了效率的同时，效果超越了图6c和图6d。原因是许多很小数量的关节点连接通道（13边数 vs 91边树），使这更容易训练收敛。
 

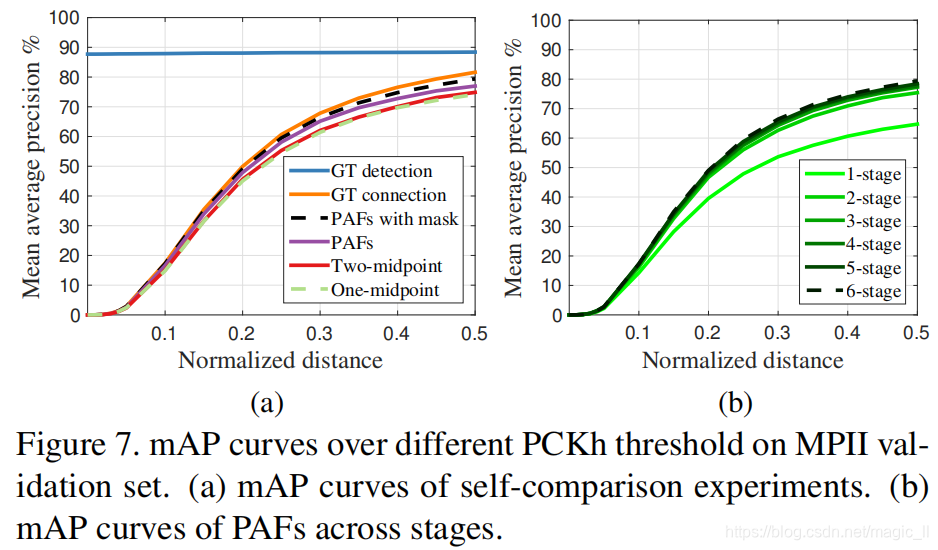
图7a展示了，基于我们验证集上的一个消融分析。对于PCKh-0.5的阈值，使用PAFs的结果比使用 中点表示的结果更好。明确的说，比单中点表示高2.9%，比双中点表示高2.3%。PAFs 同时编码了人体肢体的位置信息和方向信息，这可以更好区分出常见的肢体交叉重叠的情况，例如手臂重叠。训练中 使用未标签的人的mask 提高了性能2.3%，因为在训练损失中，避免了惩罚真实正确预测的位置。
在图7a中，在不同的PCKh阈值下 我们使用GT检测划分的mAP保持不变，这是由于没有定位错误。基于我们的关键点检测上使用GT连接，到达了81.6% mAP。值得注意，我们基于PAFs的划分算法达到了使用GT连接相似的mAP（79.4% vs 81.6%）。这表明基于PAFs的划分方式 在正确的连接检测的关键点上，是十分鲁棒的。图7b展示了不同阶段的性能的比较。在迭代优化框架下，mAP单调递增。图4展示了多个stage后的预测的质量的提升。

3.2 Results on the COCO Keypoints Challenge

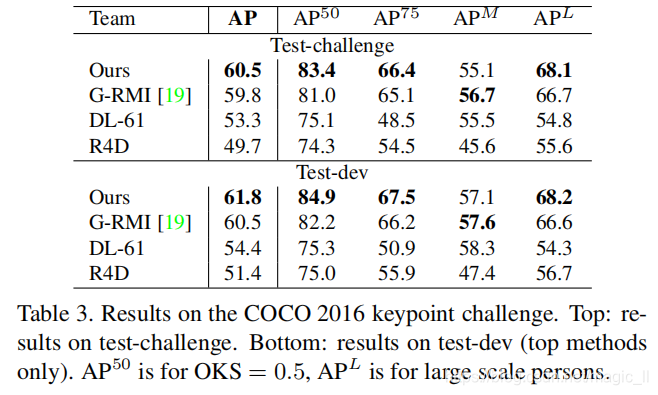
COCO训练集是由100k人的实例，其中超过1百万个关键点的标注（人体关节点)。测试集包括“测试挑战”、“测试开发”、“测试标准”，每一个包括大约20k张图片。COCO评估定义了目标关键点的相似性【the object keypoint similarity (OKS)】，同时在10个OKS阈值上使用AP，作为主要竞争指标。OKS在目标检测中扮演着相同的角色。它由人的尺度、预测点和真实点之间的距离计算而来的。表3展示了这项工作中顶尖团队的结果。
值得注意的是，在小尺寸人时，我们的方法比自上而下的方法的精度低很多。是因为我们的方法需要同时处理较大尺寸范围，其包括了图片中的所有人。相比，自上而下的方法能够重新调整每个检测区域的尺寸，到更大的尺寸，因此在较小的尺寸下面临较小的恶化。

 
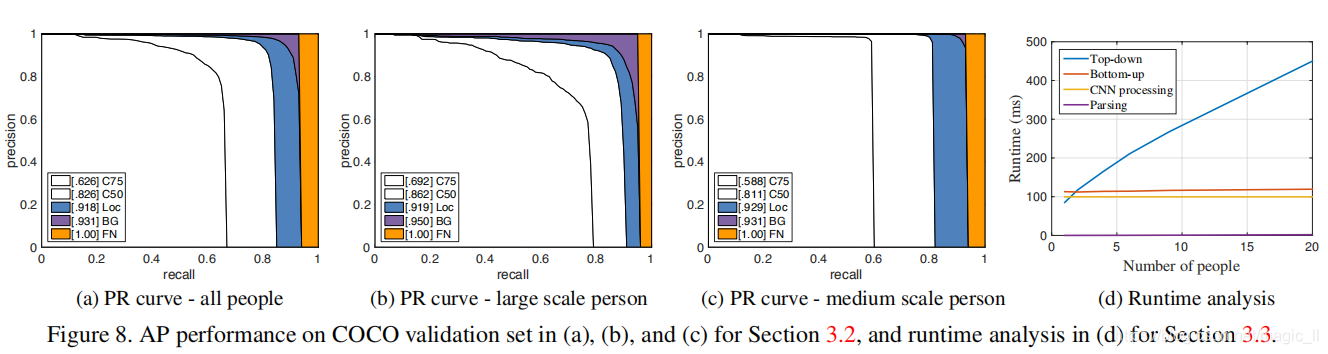
在表4中，我们报告了在COCO验证集的子集中的自我比较，随机选择的的1160张图片。如果我们使用真实边界框和单人的CPM，使用CPM 我们可以达到自上而下的方法的上限62.7%的AP。如果我们使用最先进的目标检测SSD，性能下降10%。自我比较表明了自上而下方式的性能十分依赖人体检测器。相比而言，我们自下而上方式达到了58.4%的AP。如果用我们的方法将被估计的人的区域重新缩放，然后使用CMP，将会改善我们的结果，获得了2.6% AP的提升。注意，我们仅仅更新了对两种发放一致的预测的估计，从而提高了精度和召回率。我们希望更大的尺寸搜索能够进一步的提升我们自下而上的性能。图8展示了在COCO验证集上我们方式错误的情况。大多数假阳性来源于不准确的定位，除了背景的混淆。这说明捕获空间的依赖 比识别身体部分的外观，有更多的提升空间。

3.3 运行时间分析

为了分析我们的方法的运行时间性能，我们挑选了有着巨大数量的人的视频。原始帧的尺寸是1080x1920，在测试时为了使用GPU的显存，resize到368x654。运行时间的分析在显卡为GTX-1080的笔记本上执行。在图8d中，我们用人体检测器+单人CPM作为一个自上而下的比较，其运行时间与图片中人的数量大概成正比。相比之下，我们的自下而上方法，随着人数的增减，其的运行时间增加缓慢。这个运行时间包括两部分：(1) CNN处理的运行时间，其复杂度记为 $O(1)$，为常量；(2) 多人划分时间（肢体的正确连接），其复杂度记为 $O(n^2)$，这里的n是人的数量。然而，划分时间不会是整体运行时间的主要因素，因为它比CNN处理时间少两个量级。例如，9个人肢体划分需要0.58ms，CNN需要99.6ms。我们的方法在视频有19人时，已经达到了8.8 fps的处理速度。