✅作者简介:热爱科研的Matlab仿真开发者,修心和技术同步进步,matlab项目目标合作可私信。
🍎个人主页:Matlab科研工作室
🍊个人信息:格物致知。
更多Matlab仿真内容点击👇
⛄ 内容介绍
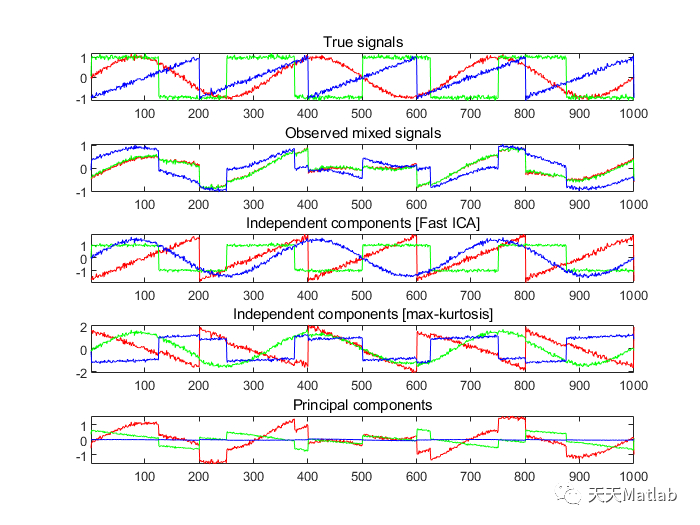
( PCA )和分析(ICA)的的的的主主主主的的的的的。。。。和和和和和和和和和在在在在在包作为函数函数实现实现实现实现实现实现实现函数函数到其中的个相相的奇异向量上上种种操作操作有效有效地地地地将将将输入输入信号分解分解分解为数据数据数据中中因此因此因此因此。。。。。分量分量分量正交正交PCA会低维表示,可以可以将以以紧密原始在在在在在在ica ica与pca的之在于在于,低维低维不一定对应于大方差方差的的方向,ica组件相反,ica组件组件最最最大中中中中中实践实践
⛄ 部分代码
函数 [Zpca, U, mu, eigVecs] = PCA(Z,r)
%
% 语法:Zpca = PCA(Z,r);
% [Zpca, U, mu] = PCA(Z,r);
% [Zpca, U, mu, eigVecs] = PCA(Z,r);
%
% Inputs: Z 是一个 dxn 矩阵,包含 n 个 d 维样本
% 数据
%
% r 是要计算的主成分数
%
% 输出:Zpca 是一个包含 r 主体的 rxn 矩阵
% components - scaled to variance 1 - of the input samples
%
% U is a d x r matrix of coefficients such that
% Zr = U * Zpca + repmat(mu,1,n);
% is the r-dimensional PCA approximation of Z
%
% mu is the d x 1 sample mean of Z
%
% eigVecs is a d x r matrix containing the scaled
% eigenvectors of the sample covariance of Z
%
% Description: Performs principal component analysis (PCA) on the input
% data
%
% Author: Brian Moore
%
% Date: April 26, 2015
% November 7, 2016
%
% Center data
[Zc, mu] = centerRows(Z);
% Compute truncated SVD
%[U, S, V] = svds(Zc,r); % Equivalent, but usually slower than svd()
[U, S, V] = svd(Zc,'econ');
U = U(:,1:r);
S = S(1:r,1:r);
V = V(:,1:r);
% 计算主成分
Zpca = S * V';
%Zpca = U' * Zc; % 等效但较慢
如果 nargout >= 4
% 缩放特征向量
eigVecs = bsxfun(@times,U,diag(S)' / sqrt(size(Z,2)));
结尾
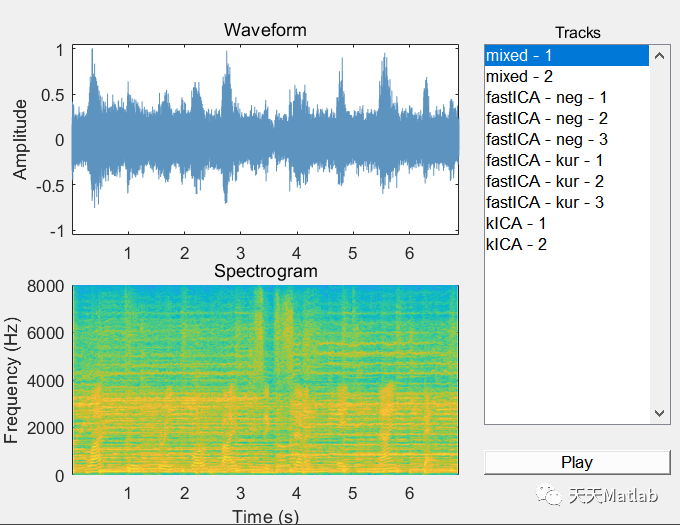
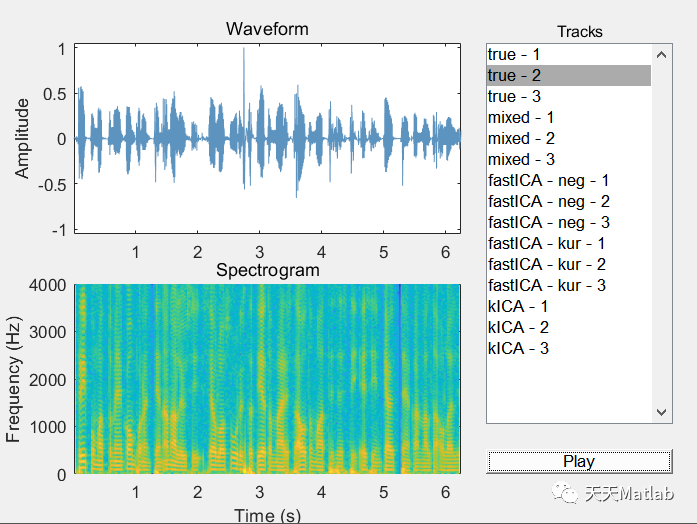
⛄ 运行结果
⛄ 参考文采
[1]冯祥,陈良彬. 基于主成分分析和独立成分分析的调节分类算法[J]. 电讯技术, 2013(7):864-867.
[2]梁胜杰,张志华,崔立林,等. 基于主成分分析与独立成分分析的降维方法[J]. 系统工程与电子技术, 2011.
⛄ Matlab代号关注
❤️部分分析引用网络文档,若有版权联盟博主删除
❤️ 关注我领取海量matlab电子书和数学模型资料