如果非要在推荐系统里找出机器学习最能大展拳脚的领域,那一定是排序部分。同属于推荐系统的召回和重排序,其算法基本上都可以用规则或者策略的方式平替,虽然效果不一定好,但可以支撑业务的正常运转。然而对于排序这一部分,可以说就是天然为了模型而生的,只有模型化的排序,才可能为广告系统和排序系统带来大的收益。
由于排序模型在推荐和广告领域有着举足轻重的地位。本章里,我们不谈具体排序方法,先从整体对排序模型进行概要了解。
排序模型的重要性
为什么排序如此重要?在广告系统中,早期排序是完全面向点击率的。按点击付费的广告,哪怕提升百分之一的点击率,都会带来大量真金白银。一次用户请求中带过来的广告位,通常只有一个(最多三个),为有限的资源位筛选出最可能带来点击的广告,是广告系统的重中之重。因此,早期广告领域的模型工程师,基本都在孜孜不倦地研究如何在排序系统中不断提升点击率。而推荐系统其实是对广告系统的沿袭,虽然推荐系统返回结果要远多于广告系统(通常有十几到几十条条),但头几条内容的作用仍然举足轻重。尤其是对新用户来说,能否吸引用户持续消费,成败可谓在此一举。
我们在最早的文章里,介绍过推荐系统线上推荐的流程:召回阶段会将全库数据精简到几十到几百个,再由排序模型进行排序,接着会根据业务逻辑重排序,最终将截断的结果呈现给用户。如果召回阶段返回了几百上千个物品,而排序性能不足以在短时间内完成,那么中间还会插入粗排模型,一般粗排模型可以看作是精排模型的精简版,或使用更少的特征,或使用更浅的网络,总之,保证系统在极短时间内能快速排完并截断,然后将结果送给精排模型。
后面的几章,笔者会介绍若干工业实践中常用的排序模型。如无特殊说明,我们所指的排序,都是指精排。
排序模型的目标
点击率排序
明确排序模型的目标之前,我们先了解下排序模型属于哪种机器学习任务。通常来说,有标签指导的主流机器学习模型大致分为两类:分类任务和回归任务(提一句,近些年兴起的强化学习并不在其中,算是第三类)。其中,分类任务是针对离散值,预测样本属于哪个或哪几个标签,常见场景如图片分类、商品类别识别、文章情感识别等;而回归任务则是针对连续值,预测样本的输出值,常见场景如房价预测、票房预测、外卖时间预估等。
那么排序模型属于哪种任务呢?既然是模型用于排序,那自然需要排序标准。业界最为常用的标准便是点击率(CTR),因此通常称排序模型为CTR模型。CTR模型以当前用户对于当前物品点击和未点击来设计目标,因此,排序模型便可看作是二元分类模型。在早期,逻辑回归模型(Logistics Regression,LR)被应用于来训练点击率指标----逻辑回归虽名为回归,其实属于分类任务。它在训练时使用二元分类目标,预测时则输出点击的概率,从而根据概率来排序项目。
多目标排序
广告的收益取决于点击和单次广告出价。因此点击率高,就意味着收益的水涨船高。但对于推荐系统来说,仅考虑点击率,则会带来较多问题。比如发布者使用美女图,或UC震惊体来诱导点击,等。一般情况下,推荐系统希望在提升用户点击率的基础上,同时提高用户的关注、点赞、评论等交互行为,从而维护良好的社区氛围。即使对于广告,只关注点击,而不关心转化,则给平台带来收益的同时,伤害的是广告主的利益。因此,多目标学习(Multi-task)这种“既要又要”的诉求,会大量存在于广告和推荐系里。
广告领域里,重排阶段广告最终排序的公式是: e c p m = p c t r k ∗ b i d ecpm = pctr^k * bid ecpm=pctrk∗bid,其中,pctr是预估CTR,由精排模型给出,bid是广告主出价。这个公式可以看作多目标任务的简单实现。它同时考虑了广告质量(CTR)和价格(bid)。公式中,k是价格挤压因子,通过对k的调节,增大或缩小排序公式中CTR部分的重要度。当k趋近于无穷时,相当于只根据点击率来排序;k为0时,相当于只根据bid来排序。根据不同时期业务需求,通过k来调整广告的排序目标:对广告质量有较高要求时,则增大CTR的比重;月底或季度底,需要对广告预算冲消费时,则减小CTR的比重。
上面这种方式其实就是多目标调和的方式,但它只是最简单的一种思路。实际上,如何更合理、更深度地融合多目标,是工业界,也是学术界对于排序研究的一个主流方向。其思路可大体分为两类:线上多目标融合和线下的多任务学习。
-
线上多目标融合:
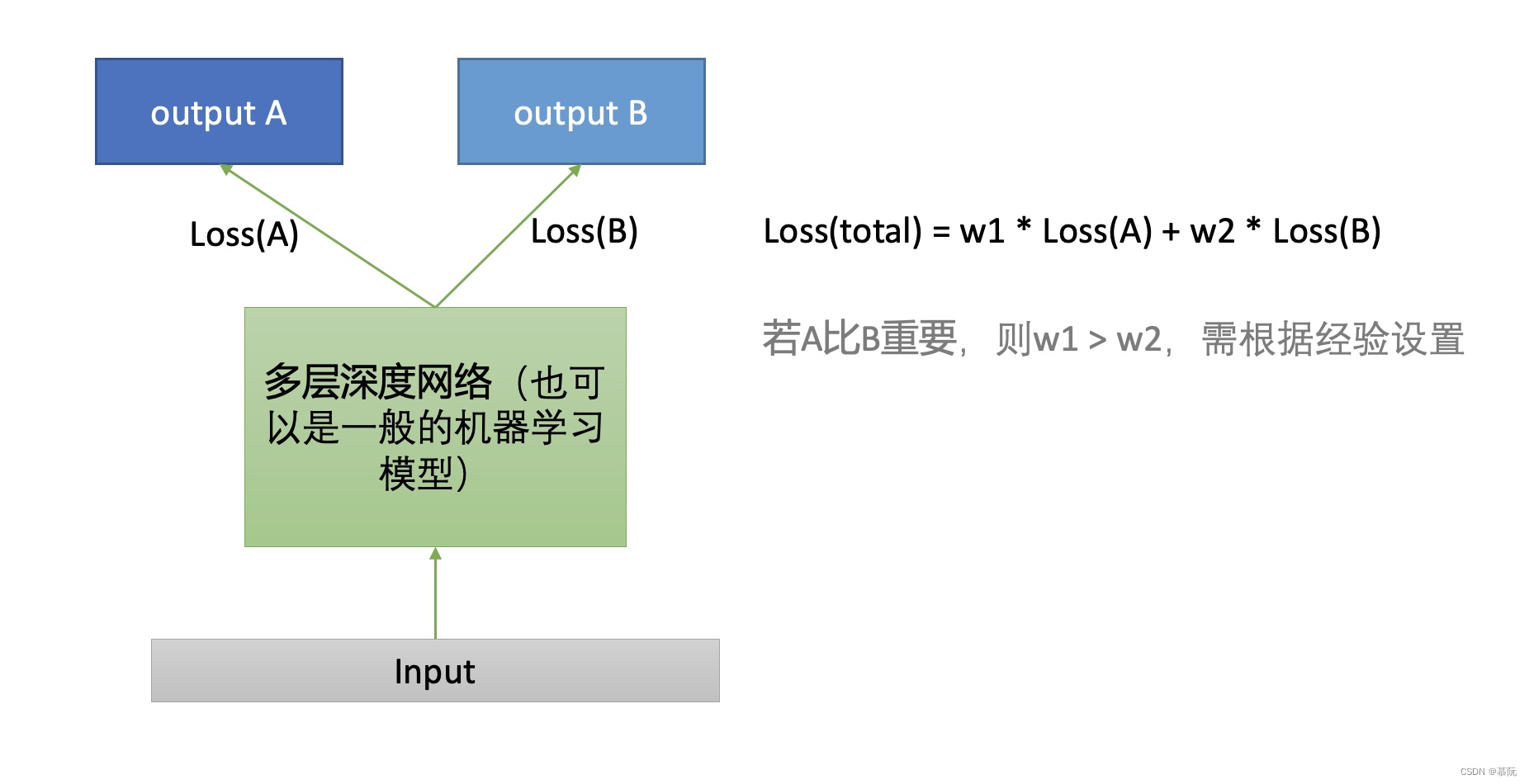
线上多目标融合是把融合的时机放在模型预测之后。线下先按照目标各自训练模型,线上每个模型分别预测打分,乘以各自权重,继而进行加和或乘积汇总。通常采用如下公式:y = ∑ i = 1 k b i ∗ ( a i + y i ) y = ∏ i = 1 k ( a i + y i ) b i \begin{align} y = \sum_{i = 1}^{k}{b_i * (a_i + y_i)} \\ y = \prod_{i=1}^{k}{(a_i+y_i)^{b_i}} \end{align} y=i=1∑kbi∗(ai+yi)y=i=1∏k(ai+yi)bi
两个公式分别代表通过加法或乘法方式进行融合。其中 a i a_i ai控制值域的中心点偏移, b i b_i bi则是对目标值进行缩放,在加法融合中, b i b_i bi表示目标得分的占比。可以根据不同目标在当前业务中的重要程度,给子目标设置不同权重。多目标融合在业界有很多案例:如快手的多目标排序 [ 1 ] ^{[1]} [1],京东的多目标模型排序 [ 2 ] ^{[2]} [2]等。实践中,固然存在人工设计目标权重的场景,但现今的大部分目标融合权重,多使用模型来训练,即超参数搜索,典型算法如交叉熵算法(Cross-Entropy Method,CEM)、进化策略(Evolutionary Strategy,ES)、贝叶斯优化(Bayes Optimization)等。
-
线下多任务学习:
- 常见的简单方法,是按照用户不同行为对样本进行赋权(如购买权重要大于点击)。模型在更新参数时,梯度乘以权重,增大了高权重样本的影响力,直观上讲,对于权重大的样本,预测错误会带来更大损失,从而在不损害或较小损害某个目标(如点击率)的基础上,更大程度地优化关注目标(如转化率);这种思路适用于大部分模型,如LR、GBDT、深度学习等。
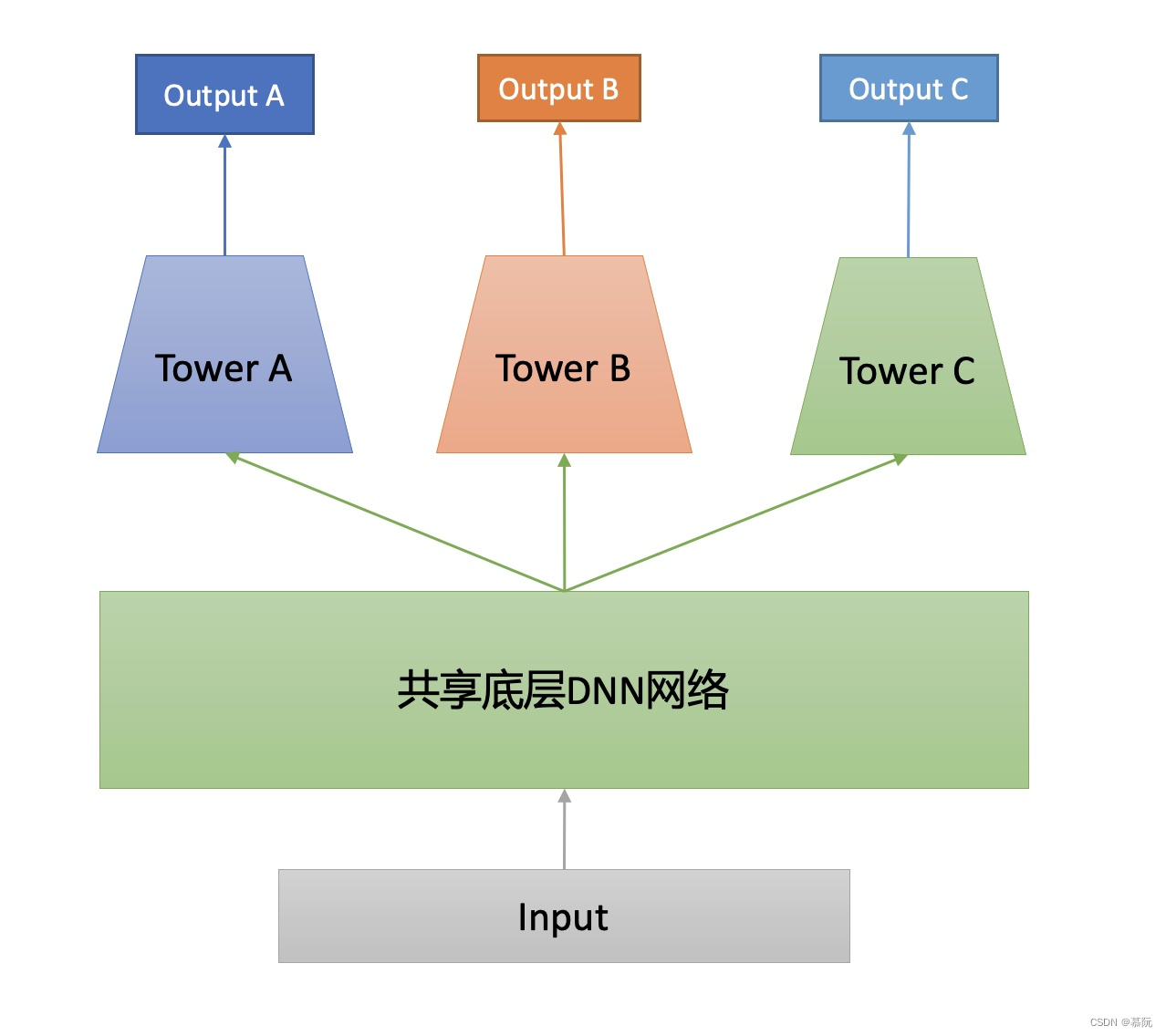
- 随着深度学习在推荐系统中的发展,一种模型设计中颇为经典的多目标任务的思路,被应用于多任务学习中。它类似于我们在之前的博客《深入浅出推荐系统(四):召回:向量化的潮流》所介绍的DSSM,即双塔模型。对于不同的目标,同样构建不同的塔。与DSSM不同的是,多目标任务在底层可以共享参数(即多塔共用同样的基建),如下图所示。其好处在于可以在学习不同目标时,通过共享参数进行知识迁移,利用其他目标学习到的知识,帮助自己进行知识学习。
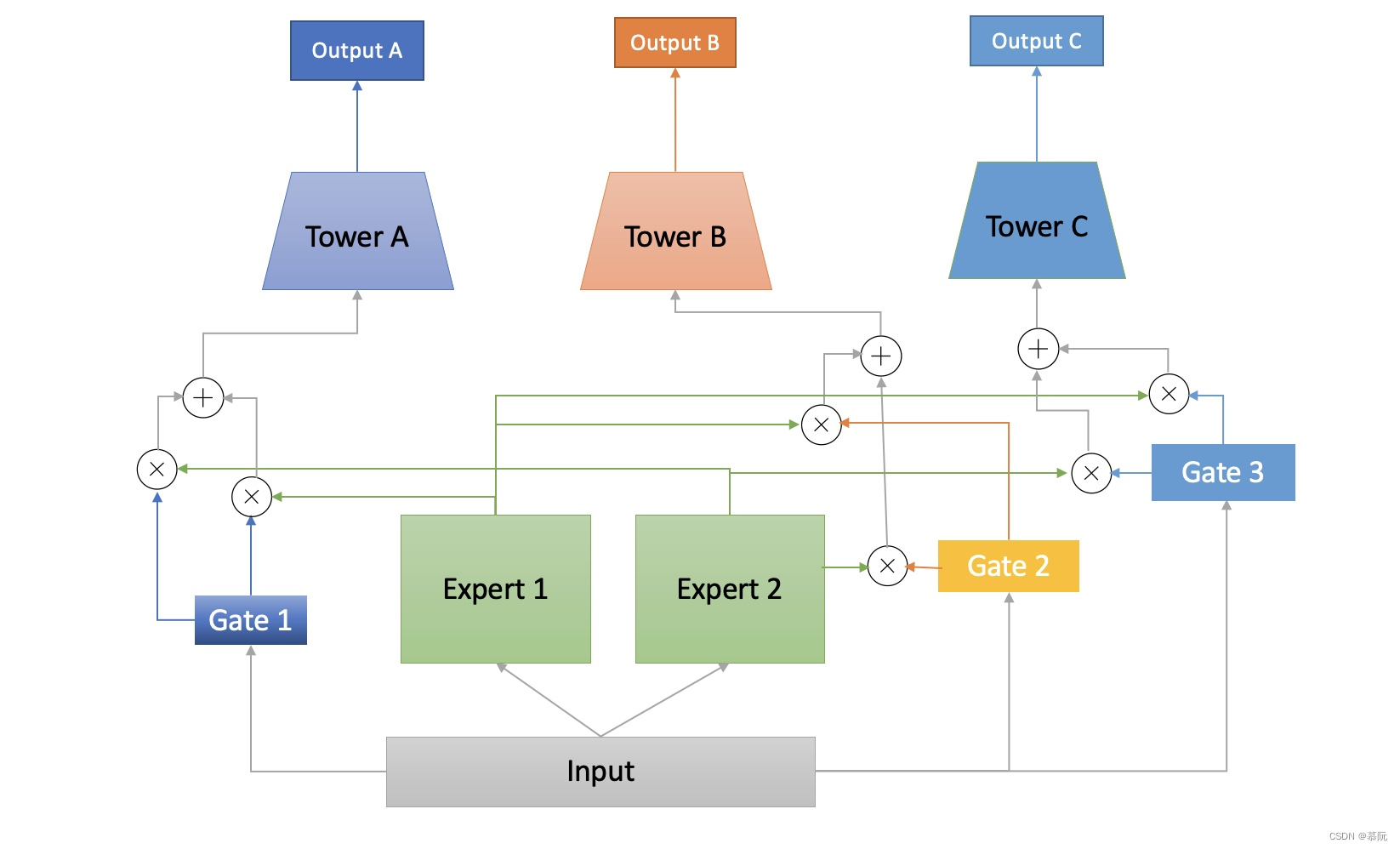
- Google在2018年发布的研究中[1],提出了MMoE架构,是多目标排序模型的另一个经典模型。模型认为多个模型共享底层基建存在一定问题:因为多个目标可能是不相关的(比如收藏和回复),那么学习到的知识可能不具备可共享性。该模型思路是:每个目标在底层分别独立训练模型(Expert),在顶层给每个塔设置一个Gate,同时将Expert输出给Gate,Gate输出每个Expert被选择的概率(每个Gate的权重和为1,实际表达的是对不同Expert的动态赋权),然后将三个Expert的输出加权求和,输出给不同的目标塔。该模型其实可以类比前面所说的策略的思路,本质上是对不同任务设置不同权重(通过gate),但该权重是通过模型训练出来的,而非手动设置的。
额外提一句,虽然Google的这个研究是基于深度学习网络来进行的,但实际上这个思路本身可以适用于其他模型。每个目标独立训练的部分其实可以使用不同的非深度模型来实现。 - 最新的研究还有如阿里的ESMM,将CTR与CVR(转化率)的预估置于同一个模型,使用两个塔,分别得到pCTR(预估点击率)和pCVR(预估转化率),再将两者相乘,就得到了pCTCVR(曝光转化率),转化的正样本同时来训练两个塔的网络,而点击的正样本则只更新点击的网络。
排序模型的任务
有了目标,则可以据此构建损失函数,损失函数度量的是预测值与真实值之间的差异,通过最小化差异,来训练构建的模型,从而得到模型的未知参数。回归问题的损失函数多采用均方误差,分类问题的损失函数多采用交叉熵(Cross-Entroy Loss Function)。
排序模型属于二分类问题,因此一般都使用交叉熵损失函数。该损失函数假设样本符合伯努利分布(0-1分布),然后求满足该分布的似然函数,最终得到相关公式如下:
l
o
g
P
(
y
∣
x
)
=
l
o
g
(
y
^
y
.
(
1
−
y
^
1
−
y
)
=
y
l
o
g
y
^
+
(
1
−
y
)
l
o
g
(
1
−
y
^
)
log P(y|x) = log(\hat{y}^y.(1-\hat{y}^{1-y})=ylog \hat{y} + (1-y)log(1-\hat{y})
logP(y∣x)=log(y^y.(1−y^1−y)=ylogy^+(1−y)log(1−y^)
其中,y为真实值(点击为1,未点击为0);
y
^
\hat{y}
y^为预测值,我们希望该函数越大越好(越大意味着预测值越逼近真实值,即y为1的时候,
y
^
\hat{y}
y^越接近1,logP(y|x)越大,反之亦然)。但损失函数是希望其越小越好,因此对上述公式取相反数,作为损失函数。令单样本的损失函数为
−
l
o
g
P
(
y
∣
x
)
-logP(y|x)
−logP(y∣x),则N个样本的总的损失函数就为:
L
=
−
∑
i
=
1
N
(
y
l
o
g
y
^
+
(
1
−
y
)
l
o
g
(
1
−
y
^
)
)
L = -\sum_{i=1}^{N}{(ylog \hat{y} + (1-y)log(1-\hat{y}))}
L=−i=1∑N(ylogy^+(1−y)log(1−y^))
有了损失函数,就可以基于这个损失函数来构建训练任务,通过梯度下降法来不断地更新模型参数,从而不断缩小损失函数,当损失函数缩小到一定程度,或迭代到指定次数,则训练完成。无论是逻辑回归还是神经网络,都可以基于这样的方法进行训练。
排序模型常见方法
工业界早期的点击率排序模型,基本都是逻辑回归(Logistics Regression,LR)。由于LR模型较为简单,因此提升模型性能的方法主要靠特征挖掘(事实上,现在有一些公司的排序模型还在使用逻辑回归,因为它真的很有用)。但逻辑回归也有一大缺点:它无法捕获特征之间的交互关系。由此衍生了FM、FFM模型,他们可以自动化地对特征进行二阶交叉组合。
之后又出现了以GBDT为代表的树模型,树模型能够对特征进行自动组合,可以进一步提升模型效果,并由此衍生了GBDT+LR的组合模型,GBDT用来产生组合特征,LR则用来做权重训练。
如今,随着深度学习的流行,从最初的Wide+Deep模型开始,此后的主流精排模型基本都是由深度学习来主导。
尽管如今的排序模型基本离不开DNN,但基础的经典模型依然存在借鉴意义。更好地理解些模型的变迁历史,比较这些模型的优劣,理解模型的演进思路,也会更好地理解推荐系统,并从全局角度来思考未来的方向。后续的几章里,我们会对这些模型一一进行详细的介绍。
参考文献
[1] 多目标排序在快手短视频推荐中的实践,郑东,
https://mp.weixin.qq.com/s/mxlecZpxXEoOe21UY_UCXQ
[2] 京东李欣如:从单目标排序到多目标模型,显著提升多业务效果,李欣如
https://zhuanlan.zhihu.com/p/428725155