前言

哪些情况下会用到前缀和算法：

1. 子数组和/子矩阵和查询：当需要频繁查询数组或矩阵中某个子数组或子矩阵的和时，可以通过预处理得到前缀和数组或前缀和矩阵，以便快速计算查询结果。

2. 连续区间和查询：类似于子数组和查询，但是只需要查询连续区间的和。通过预处理得到前缀和数组，可以在常数时间内计算出任意连续区间的和。

3. 数列差分：当需要对原数列的某个区间进行增减操作时，可以使用差分数组来记录每个位置的变化量，然后通过求前缀和得到新的数列。

4. 数列中元素频次统计：可以通过差分数组和前缀和数组来统计数列中每个元素出现的频次。

5. 数列中元素和的统计：可以通过差分数组和前缀和数组来统计数列中每个元素之前的和。

6. 数列中满足特定条件的子数组个数统计：通过差分数组和前缀和数组，可以统计满足特定条件的子数组的个数，如和为定值、长度满足某个条件等。

7. 频率计数和频率前缀和：通过差分数组和前缀和数组，可以计算某个元素的频率以及频率的前缀和，用于处理频率相关的问题。

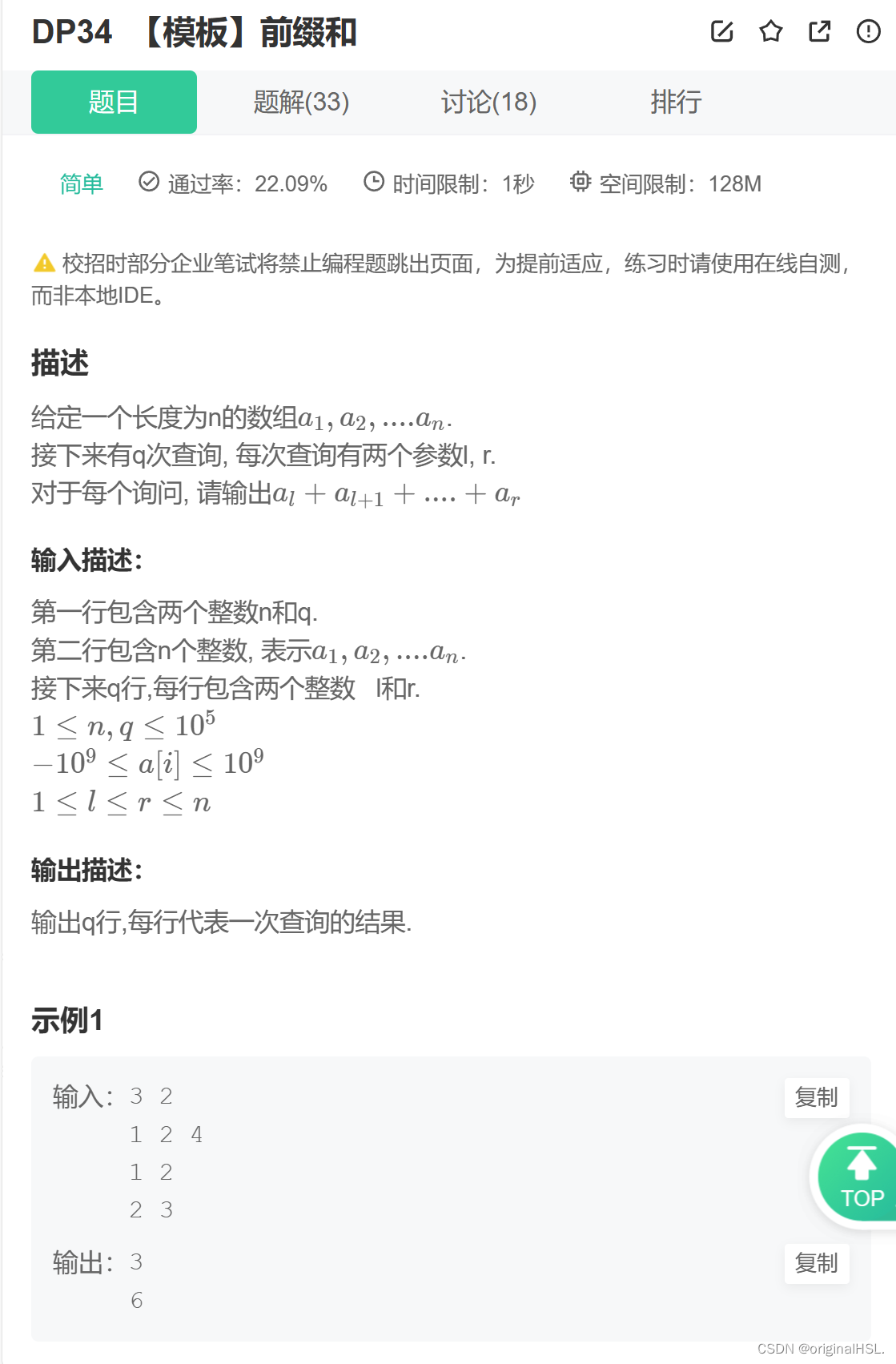
1.【模板】一维前缀和

题目地址：前缀和

1.1算法原理

1. 首先，定义了两个整数变量 n 和 q，并将它们初始化为0。这两个变量分别表示数组的长度和查询的次数。

2. 接下来定义了两个整数变量 l 和 r，用于表示查询的范围。

3. 使用 cin 输入 n 和 q 的值，分别表示数组的长度和查询的次数。

4. 创建了一个长度为 n+1 的整数向量 arr，用于存储输入的数组。

5. 使用 for 循环，从1到 n 依次输入数组的元素，并将其存储在 arr 中。

6. 创建了一个长度为 n+1 的长整型向量 dp，用于存储前缀和。

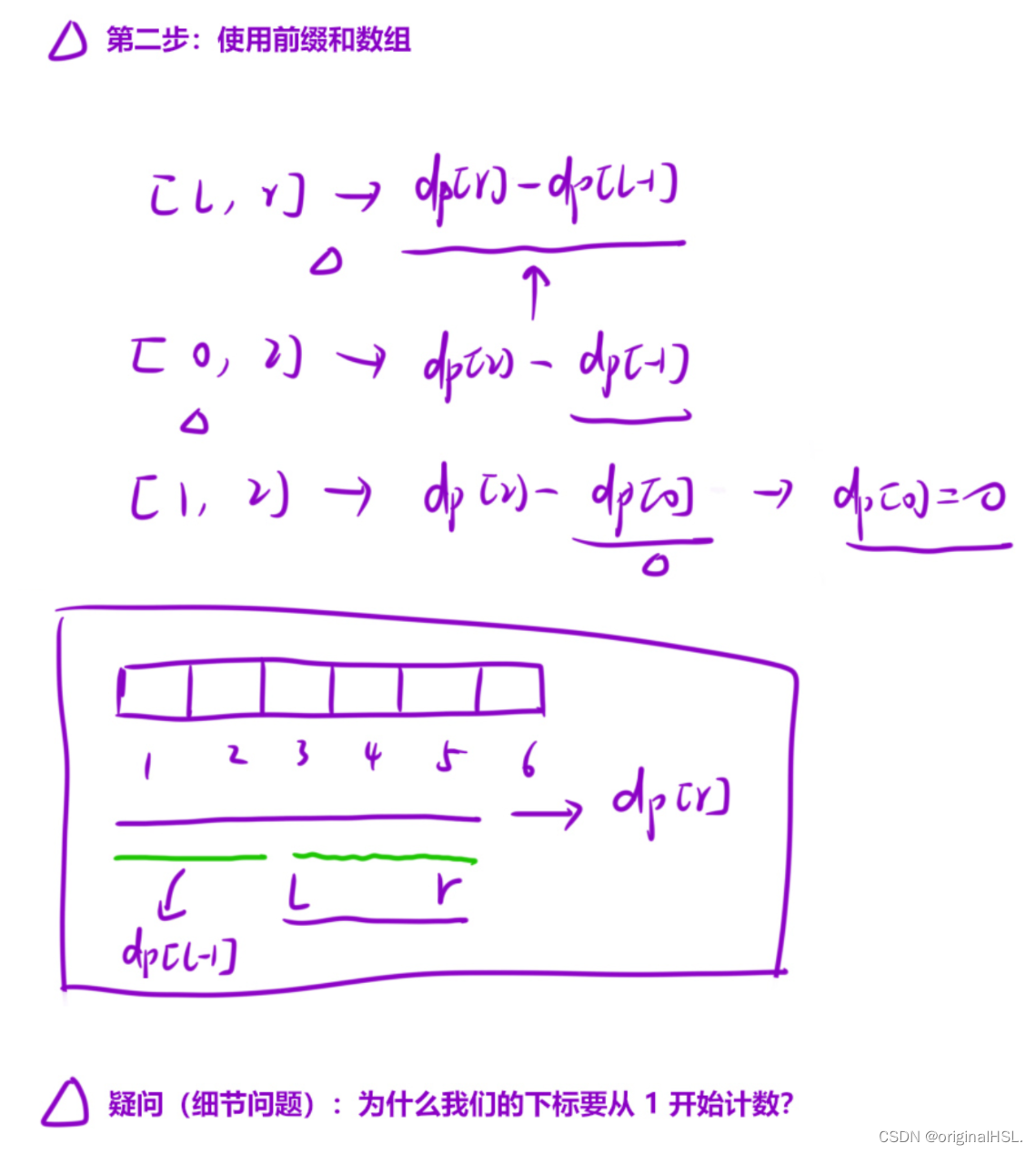
7. 使用 for 循环，从1到 n 遍历数组，并计算前缀和。具体做法是将当前元素与前一个元素的前缀和相加，然后存储在 dp 中。

8. 使用 while 循环，执行下面的操作 q 次，即进行 q 次查询。

9. 在每次查询中，使用 cin 输入查询的范围 l 和 r。这表示需要计算从下标 l 到下标 r 的子数组的和。

10. 输出 dp[r] - dp[l-1]，即数组从下标 l 到下标 r 的子数组的和。

11. 重复步骤 8 到步骤 10，直到完成所有的查询。

12. 返回0，表示程序顺利执行结束。

1.2 代码

#include <iostream>
#include <vector>
using namespace std;

int main() 
{
    int n=0,q=0;
    int l,r;
    cin>>n>>q;
    vector<int> arr(n+1);

    for(int i=1;i<=n;i++) 
    cin>>arr[i];

    //预处理一个前缀和数组
    vector<long long> dp(n+1);
    for(int i=1;i<=n;i++)
    dp[i]=dp[i-1]+arr[i];

    while(q--)
    {
        cin>>l>>r;
        cout<<dp[r]-dp[l-1]<<endl;
    }
    return 0;
}

2.【模板】二维前缀和

题目地址：二维前缀和

2.1 算法原理

1. 首先，定义了三个整数变量 m、n 和 q，并使用 cin 输入它们的值。其中，m 表示矩阵的列数，n 表示矩阵的行数，q 表示查询的次数。

2. 创建了一个二维整数向量 arr，大小为 (n+1) × (m+1)，用于存储输入的矩阵。

3. 使用两个嵌套的 for 循环，从1到 n 和从1到 m，依次输入矩阵的元素，并将其存储在 arr 中。

4. 创建了一个二维长整型向量 dp，大小为 (n+1) × (m+1)，用于存储二维前缀和。

5. 使用两个嵌套的 for 循环，从1到 n 和从1到 m，计算二维前缀和。具体做法是根据动态规划的思想，将当前位置的元素与其左边、上边和左上角位置的前缀和相加，并减去左上角位置的前缀和。将计算结果存储在 dp 中。

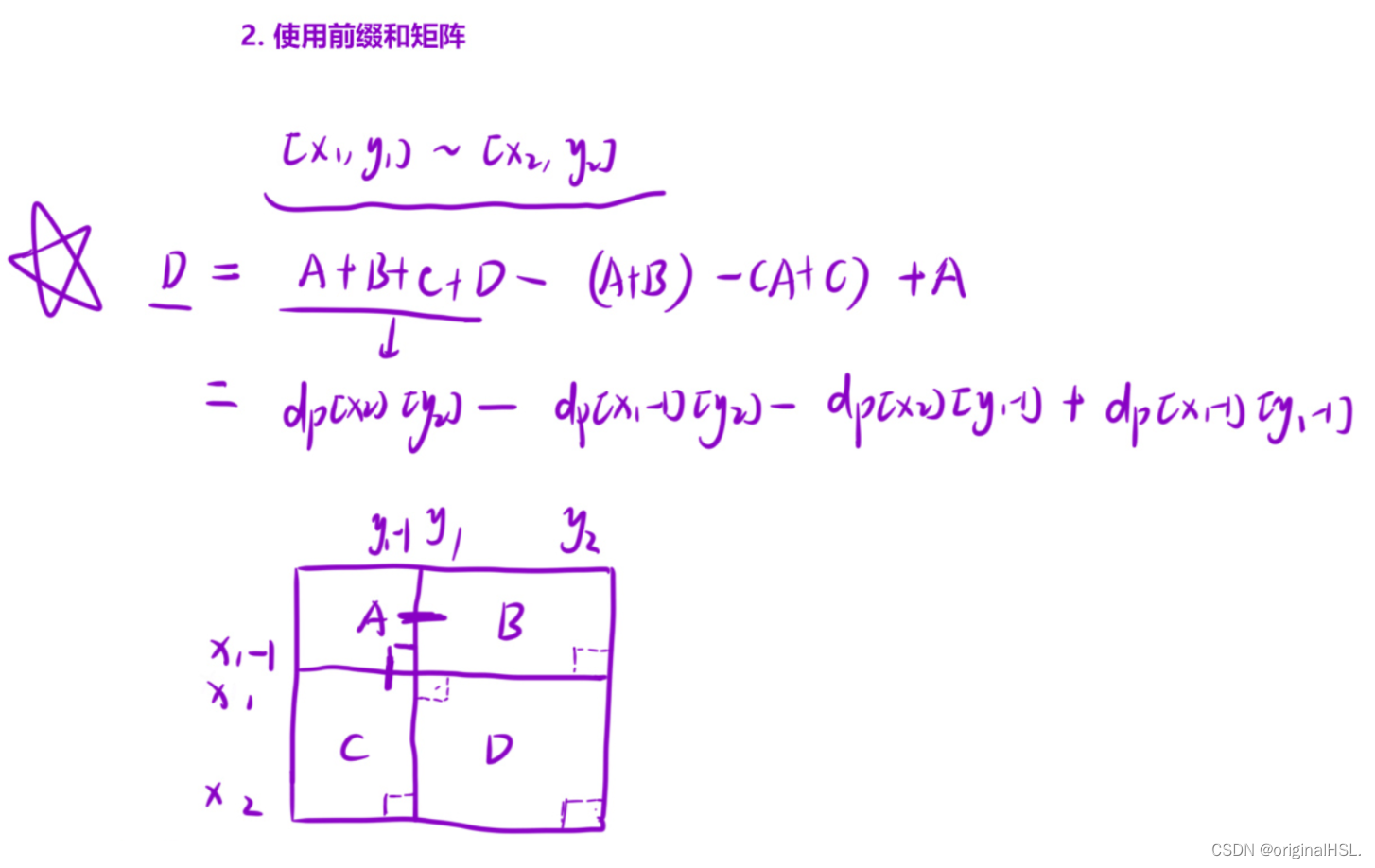
6. 在每次查询中，使用 cin 输入查询的范围，分别为起始点 (x1, y1) 和终止点 (x2, y2)。这表示需要计算从矩阵的 (x1, y1) 位置到 (x2, y2) 位置的子矩阵的和。

7. 输出 dp[x2][y2] - dp[x1-1][y2] - dp[x2][y1-1] + dp[x1-1][y1-1]，即子矩阵的和。这里的计算方式是利用二维前缀和的性质，通过相减来得到子矩阵的和。

8. 重复步骤 6 到步骤 7，直到完成所有的查询。

9. 返回0，表示程序顺利执行结束。

2.2 代码

#include <iostream>
#include <vector>
using namespace std;

int main() {
    int m,n,q;
    cin>>n>>m>>q;
    vector<vector<int>> arr(n+1,vector<int>(m+1));
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            cin>>arr[i][j];
        }
    }

    //预处理dp
    vector<vector<long long>> dp(n+1,vector<long long>(m+1));
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            dp[i][j]=dp[i][j-1]+dp[i-1][j]+arr[i][j]-dp[i-1][j-1];
        }
    }

    //使用
    int x1=0,y1=0,x2=0,y2=0;
    while(q--)
    {
    cin>>x1>>y1>>x2>>y2;
    cout<<dp[x2][y2]-dp[x1-1][y2]-dp[x2][y1-1]+dp[x1-1][y1-1]<<endl;
    }
    return 0;
}