RSA算法总结（数学知识/CTF题型）

一.RSA简介

简要概括就两句话：公钥（e）加密，私钥（d）解密。
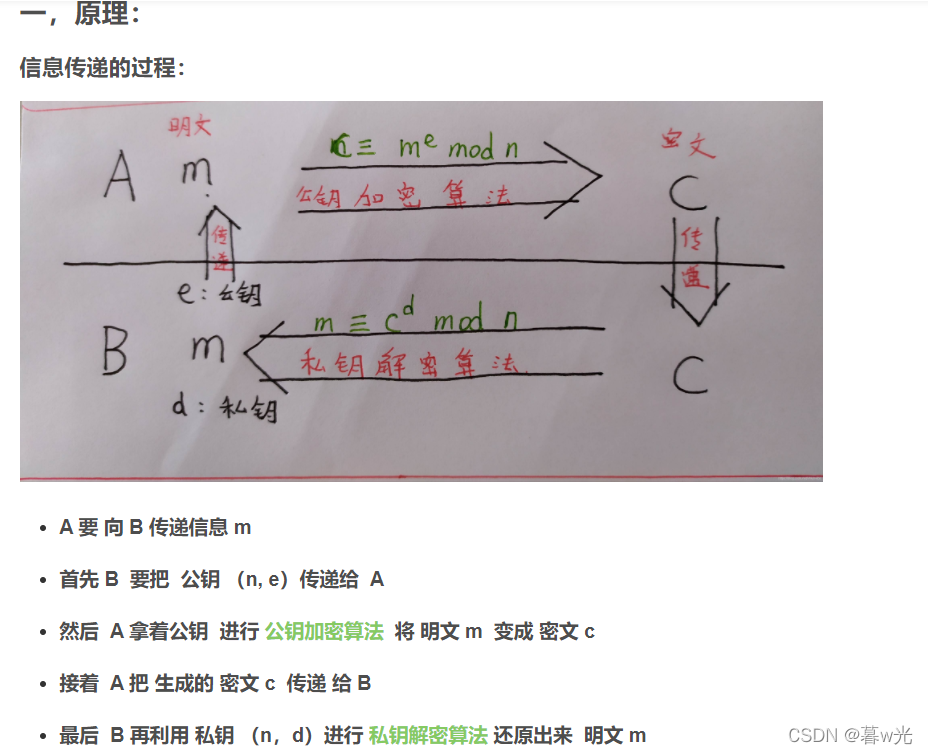
在这里插入图片描述

二.RSA过程

在这里插入图片描述

三.RSA各参数

p 和 q：两个大的质数，是另一个参数N的的两个因子。
N/n：大整数，可以称之为模数。
e 和 d：公钥和私钥，互为无反数的两个指数。
(N, e)：公钥对，有N
(N, d)：私钥对，也有N
c 和 m：密文和明文。
pow(x, y, z)：效果等效pow(x, y)1 % z，先计算x的y次方，如果存在另一个参数z，需要再对结果进行取模。
密钥长度：n以二进制表示的的位数，例如密钥长度为512代表n用二进制表示的长度为512bit。

对于RSA加密算法，公钥(N, e)为公钥，可以任意公开，破解RSA最直接（亦或是暴力）的方法就是分解整数N，然后计算欧拉函数φ(n)=(p-1) * (q-1),再通过d * e ≡ 1 mod φ(N)，即可计算出 d，然后就可以使用私钥(N, d)通过m = pow(c,d,N)解密明文。

四.数学知识

1.质数与互质数：

一个大于1的自然数，除了1和它本身外，不能被其他自然数整除（除0以外）的数称之为质数（素数）；否则称为合数。
例如，15＝3×5，所以15不是素数，13除了等于13×1以外，不能表示为其它任何两个整数的乘积，所以13是一个素数。
1不是质数，也不是合数
公约数只有1的两个数，叫做互质数。

2.同余定理：

“≡”是数论中表示同余的符号。
同余的定义如下：
给定一个正整数m，如果两个整数a和b满足a - b能被m整除，即(a - b) mod m = 0，那么就称整数a与b对模m同余，记作a ≡ b ( mod m)，同时可成立a mod m = b。
注意，同余与模运算是不同的。
显然,有如下事实：
（1）若a≡0(mod m)，则m|a；
（2）a≡b(mod m)等价于a与b分别用m去除，余数相同。

3.欧拉函数：

任意给定正整数n，计算在小于等于n的正整数之中，有多少个与n构成互质关系？计算这个值的方法就叫做欧拉函数，以φ(n)表示.
例如：在1到8之中，与8形成互质关系的是1、3、5、7，所以φ(n)=φ(8)=4。
φ(n)=(p-1)(q-1)由来：
例如：和15互质的为1,2,4,7,8,11,13,14,将15分解成3,5且两者互质，故φ(n)=φ(15)=φ(3) * φ(5)=(3-1)* (5-1)=8

4.欧拉定理：

如果两个正整数a和n两者互质，则n的欧拉函数φ(n)也可以下面的等式也成立：a^φ(n)≡1(mod n)。
也就是说，a的φ(n)次方被n除的余数为1。
这就是φ(n)与公钥e互质的原因。

5.模反元素：
根据欧拉定理，有：
a^φ(n) = a × a^(φ(n)−1)≡1(mod n)

令b=a^(φ(n)−1)，得：a×b≡1(mod n)

b就是a的模反元素 所以，如果两个正整数a和n互质，那么一定可以找到整数b使得ab-1被n整除，或者说ab被n除的余数是1。
私钥d与公钥e的乘积d*e 减去1可以被φ(n)整除，或者说ed乘积除以φ(n)的余数为1。或者说de乘积与1对模φ(n)同余，这就是私钥的d加密原理。

PS：利用两者乘积求n或由n反推p与q，通常n往往是一个 1024bit 的超大数，很难分解为两个质数。

脚本（n+e+c+p+q=m脚本）：

import libnum
from Crypto.Util.number import long_to_bytes
 
c = 0x6cd55a2bbb49dfd2831e34b76cb5bdfad34418a4be96180b618581e9b6319f86  #c：密文
n = 108539847268573990275234024354672437246525085076605516960320005722741589898641
#n = int("",16)
e = 65537
#e = int("",16)
q = 333360321402603178263879595968004169219
p = 325593180411801742356727264127253758939
 
d = libnum.invmod(e, (p - 1) * (q - 1))
m = pow(c, d, n)   # m 的十进制形式
string = long_to_bytes(m)  # m：明文
print(string)  # 结果为 b‘ m ’ 的形式

五.题型/常识等

1.最简单情况是知道p、q和公钥e，求出私钥d。

脚本如下：

import gmpy2
p = gmpy2.mpz(18443)    #初始化大整数
q = gmpy2.mpz(49891)
e = gmpy2.mpz(19)
phi_n = (p-1)*(q-1)
d = gmpy2.invert(e,phi_n)   #invert（x，m）返回y使得x * y == 1 modulo m，如果不存在y，则返回0
print("p=%s,q=%s,e=%s"%(p,q,e))
print("d is:\n%s"%d)

2.n较小时（256bit）可以rsatool或kali上yafu解密。

在线分解大素数：http://www.factordb.com/index.php