hdl_graph_slam源码解析（三）

3. scan_matching_odometry

3. scan_matching_odometry

Hello，热爱SLAM的小伙伴们，大家好！在经历了惊魂体检、春节土嗨以及爆肝论文后，越来越懒的魏小新继续给大家带来鸽了快半年的源码解析（三），期间也是十分惊讶原来自己写的东西真的有人看有人催更，这更加坚定了我和大家一起分享、解读优秀开源SLAM代码的想法，希望自己可以一直这样永葆热情。废话不多说，let’s do it！

3.3 ndt

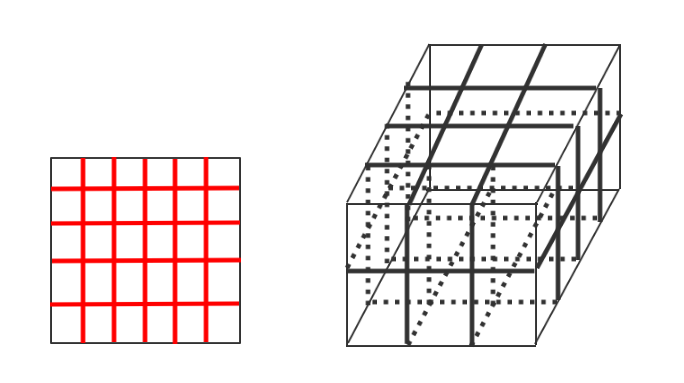
NDT，即是normal distribution transformation的缩写，翻译成中文就是正太分布变换了，哦不对，是正态分布变换！该算法的核心思想是首先将空间离散为方格，若是二维空间，则离散为栅格，若是三维空间则离散划分为立方体，没错就像切豆腐一样。然后这样做有什么好处呢，笔者觉得这样就可以将采样的点云划分到不同的网格中，这样可以很方便的描述点云的局部特性，例如点云局部的形状（直线、平面or球体）、方向（平面法向、直线方向等）。例如现在我们可以利用统计的方法分析每一块豆腐的特性。

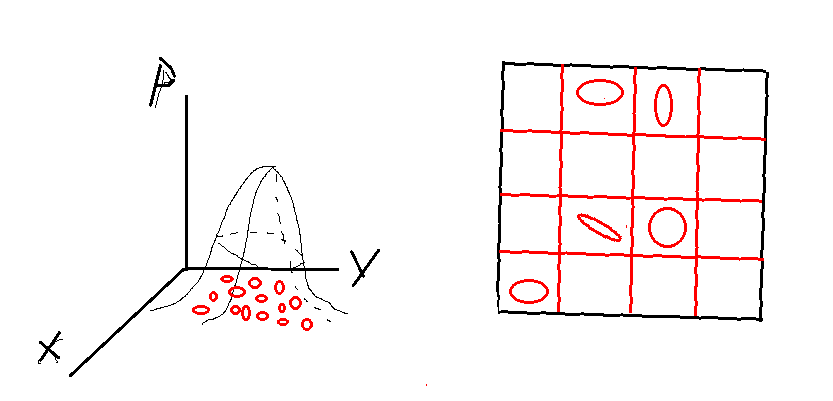
所谓正态分布变换，当然是采用正态分布的形式来拟合分析点云的局部特性。至于为什么用正态分布来描述呢？那还不是因为正态分布足够优秀！首先啊，相信大家都对正态分布的公式很熟悉，这种分布呢不仅是一种广泛存在的数据分布形式，同时又具有良好的数学性质，均值和方差（高维情况：均值向量和协方差矩阵），因此总是能在各种SLAM中的建模中看到它。其次，更有趣的是，高维情况下的协方差矩阵还能反映点云的局部特性。假设现在已知有 $N$ 个点落在了一个格子里面，为了简化问题就说是二维情况吧，然后我们可以很容易的求出这 $N$ 个点的均值 $\mu$ 和协方差矩阵 $\Sigma$ ，显然对于二维情况，该协方差矩阵为 $2\times2$ 的矩阵。若这几个点在一条直线上，则容易知道该协方差矩阵的秩为1，因此对应的特征值其中一个为0；而当这几个点近似在一条直线上时，则协方差矩阵的一个特征值会明显大于另外一个。当大致均匀分布时，两个特征值会大小类似。因此，正态分布不仅具有良好的数学性质来描述分布，还能够反映点云的局部形态。

既然正态分布可以反映点云的局部形态，自然可以利用正态分布来表示局部点云，这样就可以利用数学公式来表示一组离散的点云。

用公式表示就是：
$p(x)=\frac{1}{\sqrt{2\pi|\Sigma|}}\exp\{-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\}$

3.4 ndt matching

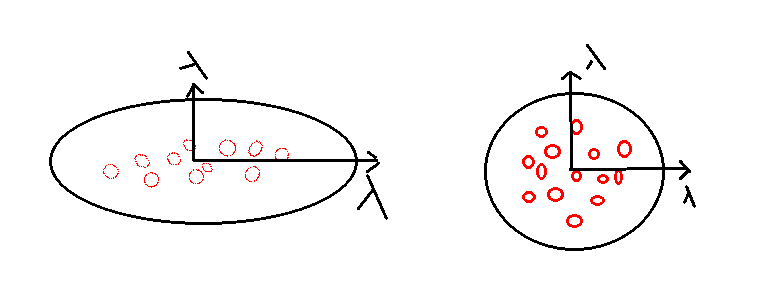
上一节中我们说可以用正态分布来拟合表示点云，这种方法可以很好的描述点云的局部形态。既然本节的主题是scan matching odometry，那么肯定要想怎么把这种表示方法应用到点云配准，进而用到激光里程计中呢？如下图所示，图中左侧是用正态分布拟合给定参考点云（上一时刻的激光扫描）后的示意图，图中红色椭圆是高斯分布对应的协方差椭圆。图中右侧当前时刻的激光扫描（目标点云），怎样利用ndt方法确定两组点云对应的位姿变换矩阵 $T$ 呢？

对于目标点云中的一点，我们可以根据当前假设的位姿变换矩阵 $T$ 计算其在参考点云坐标系内的坐标，并根据该坐标确定其在参考点云中对应的正态分布，则可以根据正态分布的概率计算方法，计算该点满足对应正态分布的概率 $p_{\mu,\Sigma}(x)$ 。则计算完目标点云中所有的点后，可以得到这样一个联合概率：
$p=\prod_{i=1}^{N}p_{i}(Tx)_{\mu_i,\Sigma_i}$
由极大似然估计，可以得到对位姿变换矩阵 $T$ 的估计：
$T^*=\arg \max_T p$
接下来就可以利用一个常用的技巧，即对高斯分布取一个negative-log，就可以将上式转化为：
$T^*=\arg \min_T \{const.+\sum_{i=1}^{N}\frac{1}{2}(Tx-\mu)^T\Sigma^{-1}(Tx-\mu)\}$
然后就可以利用一些非线性优化的算法对上式进行求解。好了，NDT matching的基本思路就是这样的了。关于NDT公式的详细推导和改进，建议参考原博士论文：The Three-Dimensional Normal-Distributions Transform — an Efficient Representation for Registration, Surface Analysis, and Loop Detection。事实上，上式的目标函数容易受野值点影响，因此原论文对高斯分布进行了一些改进。话不多说，直接撸源码吧，读源码总是能更好的理解算法，这里我们借鉴pcl对ndt的实现源码。
首先来看下这个类都有哪些成员变量：

TargetGrid target_cells_;	//正态分布（均值和协方差矩阵）表示的目标点云
float resolution_;			//体素的尺寸
double step_size_;			//优化算法中的最大步长
double outlier_ratio_;		//点云中野值点的比例
double gauss_d1_,gauss_d2_;	//两个正态分布相关的常数
double trans_probability_;	//ndt mathcing的概率
//newton-method优化中的梯度以及Hessian阵
Eigen::Vector3d j_ang_a_, j_ang_b_, j_ang_c_, j_ang_d_, j_ang_e_, j_ang_f_, j_ang_g_, j_ang_h_;	//梯度
Eigen::Vector3d h_ang_a2_, h_ang_a3_, h_ang_b2_, h_ang_b3_, h_ang_c2_, h_ang_c3_,h_ang_d1_, h_ang_d2_, h_ang_d3_, h_ang_e1_, h_ang_e2_, h_ang_e3_, h_ang_f1_, h_ang_f2_, h_ang_f3_;					//塞黑矩阵
Eigen::Matrix<double, 3, 6> point_gradient_;	//一阶导数
Eigen::Matrix<double, 18, 6> point_hessian_;	//二阶导数

除了以上所示的成员变量，还有来自继承于父类Registration中的成员变量，如最大迭代步数 $_ max\_iteration\_$ 以及更新阈值 $_ transformation\_epsilon\_$ 等。
接下来我们就要看下计算位姿变换矩阵的函数 $c o m p u t e T r a n s f o r m a t i o n ()$ :

template<typename PointSource,typename PointTarget> void
pcl::NormalDistributionsTransform<PointSource,PointTarget>::computeTransformation(PointCloudSource &output,const Eigen::Matrix4f &guess){}

这个函数就是pcl中ndt算法中最主要的部分了，即根据输入的source和target点云，计算两组点云的位姿变换矩阵。函数内部首先进行了一些初始化工作，例如

nr_iterations_=0;	//初始化迭代次数
converged_=false;	//算法收敛标识符
//将预先假设的位姿变换矩阵guess应用到output点云,以便进行近邻搜索
transformPointCloud(output, output, guess);
//将输入的位姿变换矩阵转换为6维的向量 T->(x,y,z,alpha,beta,gamma)
Eigen::Transform<float, 3, Eigen::Affine, Eigen::ColMajor> eig_transformation;
eig_transformation.matrix () = final_transformation_;
Eigen::Matrix<double, 6, 1> p, delta_p, score_gradient;
Eigen::Vector3f init_translation = eig_transformation.translation ();					//初始位移
Eigen::Vector3f init_rotation = eig_transformation.rotation ().eulerAngles (0, 1, 2);	//初始旋转
p << init_translation (0), init_translation (1), init_translation (2),
init_rotation (0), init_rotation (1), init_rotation (2);
//计算初始时刻的梯度和塞黑矩阵
score = computeDerivatives (score_gradient, hessian, output, p);

接下来就是函数的主部分了，一个大大的循环：

while(!converged_){
	previous_transformation_ = transformation_;		//保存之前的变换矩阵
	//求解newton-method的下降方向,H\delta_p=-g，其中H为塞黑矩阵，g为梯度向量
	Eigen::JacobiSVD<Eigen::Matrix<double, 6, 6> > sv (hessian, Eigen::ComputeFullU | Eigen::ComputeFullV);
	delta_p = sv.solve (-score_gradient);
	//利用线搜索方法求解步长alpha
	delta_p.normalize ();
    delta_p_norm = computeStepLengthMT (p, delta_p, delta_p_norm, step_size_, transformation_epsilon_ / 2, score, score_gradient, hessian, output);
    delta_p *= delta_p_norm;
    //更新变换矩阵和向量p
    transformation_ = (Eigen::Translation<float, 3> (static_cast<float> (delta_p (0)), static_cast<float> (delta_p (1)), static_cast<float> (delta_p (2))) *
                       Eigen::AngleAxis<float> (static_cast<float> (delta_p (3)), Eigen::Vector3f::UnitX ()) *
                       Eigen::AngleAxis<float> (static_cast<float> (delta_p (4)), Eigen::Vector3f::UnitY ()) *
                       Eigen::AngleAxis<float> (static_cast<float> (delta_p (5)), Eigen::Vector3f::UnitZ ())).matrix ();
    p = p + delta_p;
    //判断是否收敛或者达到最大迭代步数
    if(nr_iterations_ > max_iterations_ ||
        (nr_iterations_ && (std::fabs (delta_p_norm) < transformation_epsilon_))){
    converged_ = true;
    }
    nr_iterations_++;
}

整个ndt代码的流程就是这样的，至于怎样根据目标函数计算当前的梯度向量和塞黑矩阵，就不在这里说啦。感兴趣的可以自己取看一下，在pcl中的ndt.hpp源码中都说明的很清楚。ndt的主要问题是其计算效率不高，很难满足实时性要求。用过autoware的同学应该都知道用ndt进行里程计计算时有多慢。
不过好在，已经有大神实现了openmp加速版本的ndt算法，并在github上开源，跑起来速度快的不要不要的，下面就一起来看一下吧。

3.5 ndt-omp

相比如原始的ndt算法，ndt-omp主要对ndt中计算梯度以及hessian矩阵进行了多线程优化。其能进行多线程优化的原因在于ndt的目标函数是由一系列子函数的和构成的，而每一个子函数其实是一个扫描点落在最近cell的概率，因此可以分别计算每一个子函数的梯度和hessian矩阵，最后再进行求和。
$F=\sum_{i=1}^{N}p_i(T(x_i,p))$
$\frac{\partial F}{\partial p}=\sum_{i=1}^{N}\frac{\partial p_i}{\partial p}, H=\frac{\partial^2F}{\partial p^2}=\sum_{i=1}^{N}\frac{\partial^2 p_i}{\partial p^2}$
其核心代码如下：

template<typename PointSource, typename PointTarget> double
pclomp::NormalDistributionsTransform<PointSource, PointTarget>::computeDerivatives(Eigen::Matrix<double, 6, 1> &score_gradient,
	Eigen::Matrix<double, 6, 6> &hessian,
	PointCloudSource &trans_cloud,
	Eigen::Matrix<double, 6, 1> &p,
	bool compute_hessian){
	#pragma omp parallel for num_threads(num_threads_) schedule(guided, 8)
	for (int idx = 0; idx < input_->points.size(); idx++)
	{
		int thread_n = omp_get_thread_num();

		// Original Point and Transformed Point
		PointSource x_pt, x_trans_pt;
		// Original Point and Transformed Point (for math)
		Eigen::Vector3d x, x_trans;
		// Occupied Voxel
		TargetGridLeafConstPtr cell;
		// Inverse Covariance of Occupied Voxel
		Eigen::Matrix3d c_inv;

		// Initialize Point Gradient and Hessian
		Eigen::Matrix<float, 4, 6> point_gradient_;
		Eigen::Matrix<float, 24, 6> point_hessian_;
		point_gradient_.setZero();
		point_gradient_.block<3, 3>(0, 0).setIdentity();
		point_hessian_.setZero();

		x_trans_pt = trans_cloud.points[idx];

		auto& neighborhood = neighborhoods[thread_n];
		auto& distances = distancess[thread_n];

		// Find nieghbors (Radius search has been experimentally faster than direct neighbor checking.
		switch (search_method) {
		case KDTREE:
			target_cells_.radiusSearch(x_trans_pt, resolution_, neighborhood, distances);
			break;
		case DIRECT26:
			target_cells_.getNeighborhoodAtPoint(x_trans_pt, neighborhood);
			break;
		default:
		case DIRECT7:
			target_cells_.getNeighborhoodAtPoint7(x_trans_pt, neighborhood);
			break;
		case DIRECT1:
			target_cells_.getNeighborhoodAtPoint1(x_trans_pt, neighborhood);
			break;
		}

		double score_pt = 0;
		Eigen::Matrix<double, 6, 1> score_gradient_pt = Eigen::Matrix<double, 6, 1>::Zero();
		Eigen::Matrix<double, 6, 6> hessian_pt = Eigen::Matrix<double, 6, 6>::Zero();

		for (typename std::vector<TargetGridLeafConstPtr>::iterator neighborhood_it = neighborhood.begin(); neighborhood_it != neighborhood.end(); neighborhood_it++)
		{
			cell = *neighborhood_it;
			x_pt = input_->points[idx];
			x = Eigen::Vector3d(x_pt.x, x_pt.y, x_pt.z);

			x_trans = Eigen::Vector3d(x_trans_pt.x, x_trans_pt.y, x_trans_pt.z);

			// Denorm point, x_k' in Equations 6.12 and 6.13 [Magnusson 2009]
			x_trans -= cell->getMean();
			// Uses precomputed covariance for speed.
			c_inv = cell->getInverseCov();

			// Compute derivative of transform function w.r.t. transform vector, J_E and H_E in Equations 6.18 and 6.20 [Magnusson 2009]
			computePointDerivatives(x, point_gradient_, point_hessian_);
			// Update score, gradient and hessian, lines 19-21 in Algorithm 2, according to Equations 6.10, 6.12 and 6.13, respectively [Magnusson 2009]
			score_pt += updateDerivatives(score_gradient_pt, hessian_pt, point_gradient_, point_hessian_, x_trans, c_inv, compute_hessian);
		}

		scores[thread_n] += score_pt;
		score_gradients[thread_n].noalias() += score_gradient_pt;
		hessians[thread_n].noalias() += hessian_pt;
	}
	//
	for (int i = 0; i < num_threads_; i++) {
		score += scores[i];
		score_gradient += score_gradients[i];
		hessian += hessians[i];
	}
}

好了，本节关于ndt和ndt-omp的介绍就到这里了。下一节中，我们将对hdl_graph_slam中的地面检测以及回环检测部分代码进行解析。