全文链接:https://tecdat.cn/?p=37019
分析师:Haopeng Li
随着我国股票市场规模的不断扩大、制度的不断完善,它在金融市场中也成为了越来越不可或缺的一部分。
【视频讲解】神经网络、Lasso回归、线性回归、随机森林、ARIMA股票价格时间序列预测
基于此,选择合适的模型对股票价格进行精准、可靠的预测变得愈加重要。因为股票市场容易受到经济、政策、心理等多种相关因素的影响,是一个极其复杂的非线性系统,再加上每天大量投资者进行交易产生了非常庞大的交易数据需要处理、增添了股价预测的难度,所以传统的统计方法由于其在适应性、学习能力以及容错能力等方面的局限性,应用在股价预测问题上的结果往往差强人意。而计算机技术与机器学习算法的发展为股价预测开辟了一条新的道路,取得了不俗的成果。BP神经网络就是其中较成熟、应用较广泛的模型之一。选择合适的模型输入变量与优化算法来提高模型与预测的精确度也越来越不可或缺。
数据源准备
数据来自国泰安数据库,选取了中国平安(601318)个股从2017年2月16日到2021年2月16日的日开盘价、日最高价、日最低价、日收盘价、日成交量和日成交额的数据。
特征转换
计算了24个股价相关的技术指标,例如心理线(PSY= 近n
日内上涨总天数/n*100
)、布林线(一共含有三条线:中轨线 =
n
日的移动平均;下轨线 =
中轨线-m*n
日收盘价的标准差;上轨线 =
中轨线+m*n
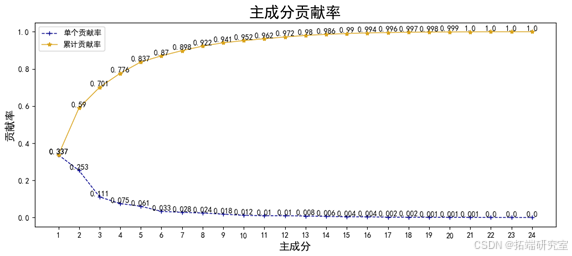
日收盘价的标准差),与开盘价、成交量等一共30个指标作为BP神经网络模型的输入变量,并用主成分分析的方法选取了6个主成分,总贡献率达到了0.87。
之后对数据进行了数据归一化,并选择五天的股票相关指标作为模型的输入变量。
构造
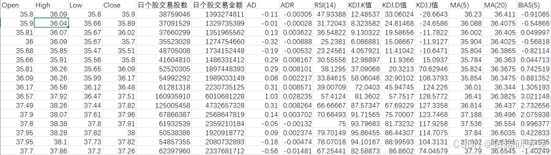
以上说明了如何抽取相关特征,我们大致有如下训练样本(只列举部分特征)。
主成分分析前:
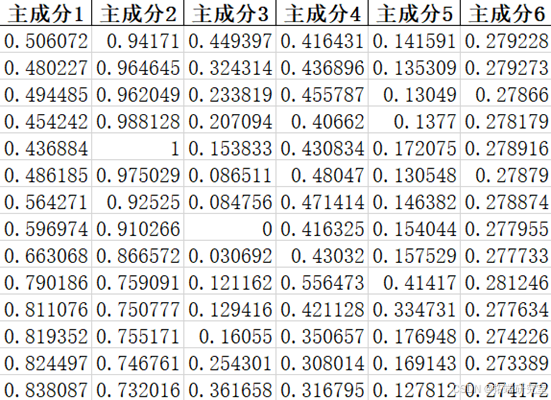
主成分分析并数据归一化后:
划分训练集和测试集
将2017年2月16日至2020年5月12日的数据划分为训练集,2020年5月12日至2021年2月16日的数据划分为测试集;其中训练集部分使用5重交叉验证的方法划分验证集来探寻模型的最优参数。经反复多次试验发现网络在1000次之内便能收敛,因此将网络的学习迭代次数设为1000次。为了减小偶然性、增加可信度,本文在验证集与测试集上均重复5次独立试验,取5次试验平均的MSE与MAE
作为最终的评价结果来比较不同参数与模型的拟合效果。
建模
BP神经网络模型
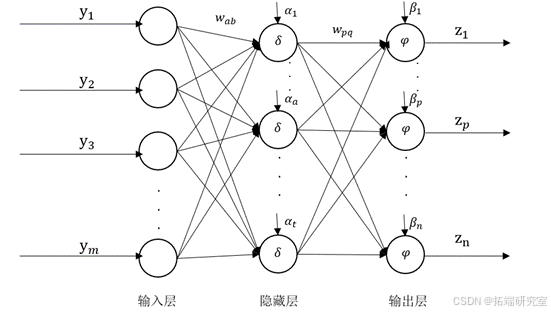
BP神经网络属于有监督的多层前馈神经网络中的一种,该网络的训练特点为输入工作信号的正向传播与反馈误差信号的反向传递。在正向传播的过程中,输入的工作信号从输入层进入网络,在经过各层的加权变换与激活函数变换后抵达输出层;在这一过程中整个网络的阈值和权值是不进行更新的,且每一层神经元的状态只收到上一层神经元状态的影响。在反向传递的过程中,根据MSE指标计算网络实际输出与期望输出之间的误差,根据该误差反向逐层修改网络的权值与阈值,使得网络的实际输出不断向期望输出逼近。经过上述两个步骤的反复迭代,网络的权值与阈值最终会收敛,学习过程就会停止。1989年Robert Hecht-Nielsen曾证明含有一层隐层的BP神经网络就可以无线逼近任意闭区间内的任意一个连续函数,因此三层BP神经网络便能够实现任意的m
维到n
维的映射。使用三层BP网络来预测股价。
Lasso回归
假定因变量y是多个自变量x1,…,xp(p≥2)
和随机误差项ε
的线性函数,则多元线性回归模型可以表示为:
y=β0+β1x1+…+βpxp+ε=Xβ+ε
其中,y为随机变量,x1,…,xp(p≥2)
为确定性的自变量,ε~N(0,σ2)
为随机的误差项,β0,..., βp
为回归系数。则多元线性回归模型的目标函数为: minβ||y-Xβ||2
在其中加入L1范数惩罚项则得到具有变量选择特征、可以得到稀疏解的Lasso回归模型:
minβ{||y-Xβ||2+λ|β|1}
模型优化
特征提取,数据降维,参数调参。
选择Adam优化算法
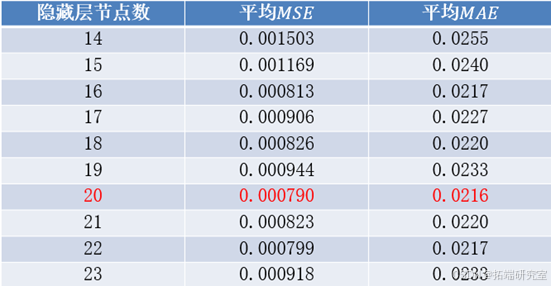
- 隐藏节点的确定
使用公式t=m+n+τ确定隐藏层的最优节点个数范围(其中,t
表示隐藏层节点数,m
表示输入层节点数,n
表示输出层节点数,τ
表示1-10之间的常数),因为输入层节点数为150,输出层节点数为1,因此隐藏层的节点数范围为[14,23]。令隐藏层的激活函数为sigmoid函数,输出层的激活函数为Leaky Relu函数,Adam算法初始的学习率设为0.01
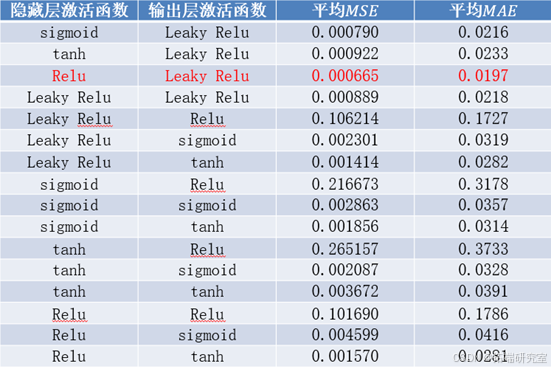
- 激活函数的确定
- 初始学习率的确定
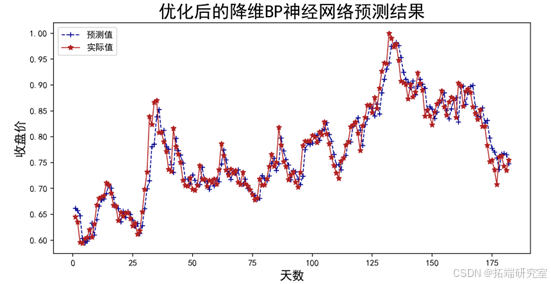
在此案例中,使用Adam算法优化的主成分分析降维的BP神经网络模型预测效果最好,在测试集上拟合的平均MSE为0.000641,平均MAE
为0.019441
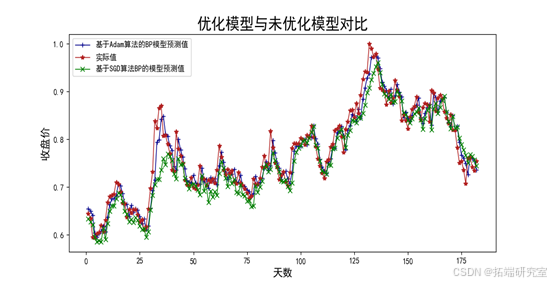
Adam优化算法的预测效果也要比SGD优化算法的预测效果好。
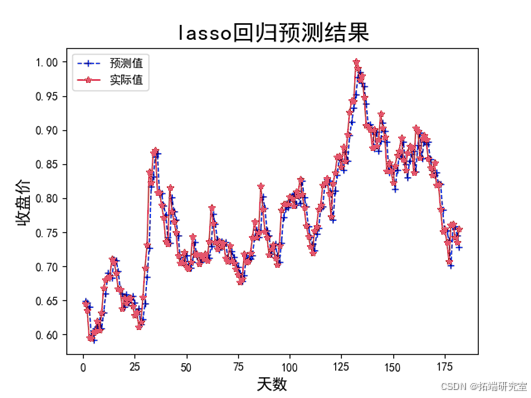
Lasso模型因为自身带有变量选择作用,应用在未降维的数据上的效果要比降维数据效果要好,因为在主成分分析降维时会损失一部分原始信息。最终模型选择变量如下所示:
模型预测结果也较好,平均MSE为0.000681,平均MAE
为0.0202。
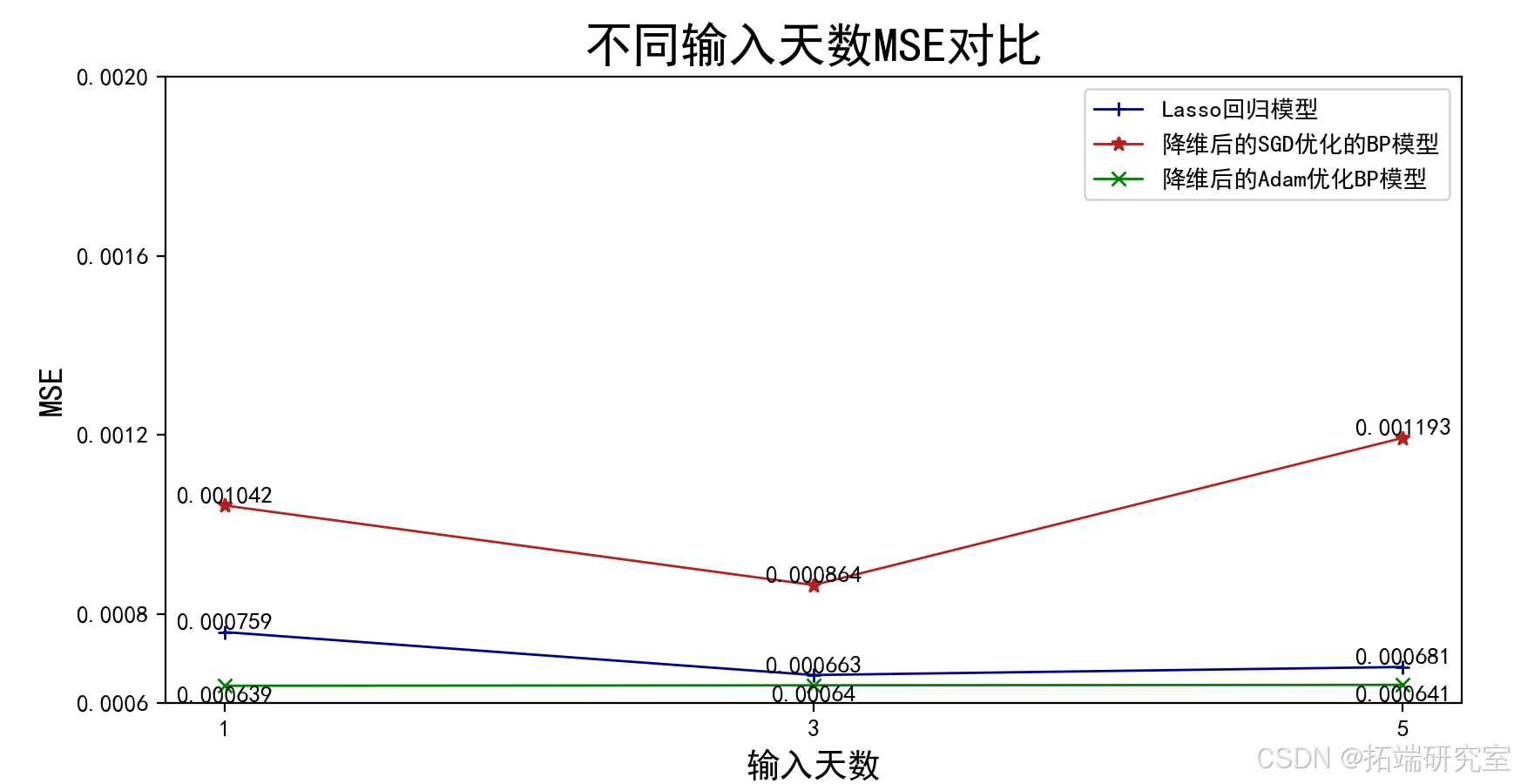
最终因为输入天数的确定具有主观性,因此尝试改变输入天数与训练集大小来观察BP神经网络模型的稳定性。
可以看到降维后的Adam优化BP神经网络模型较稳定,且模型的误差基本都随着输入天数的增加先下降再上升,这是因为当输入天数增加时最开始模型获取的有效信息增加,使模型训练得更加精确,拟合效果更好;但随着输入天数增加过多,新增的股价数据是较久远缺少时效性的数据,提供的干扰信息多于有效信息,因此模型的误差会随后增大。
但市场股价信息只是影响股票价格的一部分因素,更适用于短期股价预测;在中长期股价预测中,要考虑的因素还有很多,例如股票的基本面因素,包括宏观经济分析(CPI、GDP、通货膨胀率)、中观经济分析(企业所处的行业相关的情况)和微观经济分析(企业内部运营情况)三大方面的内容。
接下来我们一个实例包含代码和数据来演示如何用神经网络、Lasso回归、线性回归、随机森林进行股票价格预测。
基于神经网络、Lasso回归、线性回归、随机森林对大型科技股价格预测
数据选择
该数据集包括 14 家不同科技公司的每日股价和交易量,包括苹果 (AAPL)、亚马逊 (AMZN)、Alphabet (GOOGL) 和 Meta Platforms (META) 等
数据导入
数据的时间序列可视化
unique_symbols = stock['stock_symbol'].unique()
colors = ['red', 'blue', 'green', 'purple', 'grey', 'brown', 'cyan', 'magenta', 'yellow', 'black', 'orange', 'pink', '#ADD8E6', '#90EE90']
color_palette = {symbol: colors[i % len(colors)] for i, symbol in enumerate(unique_symbols)}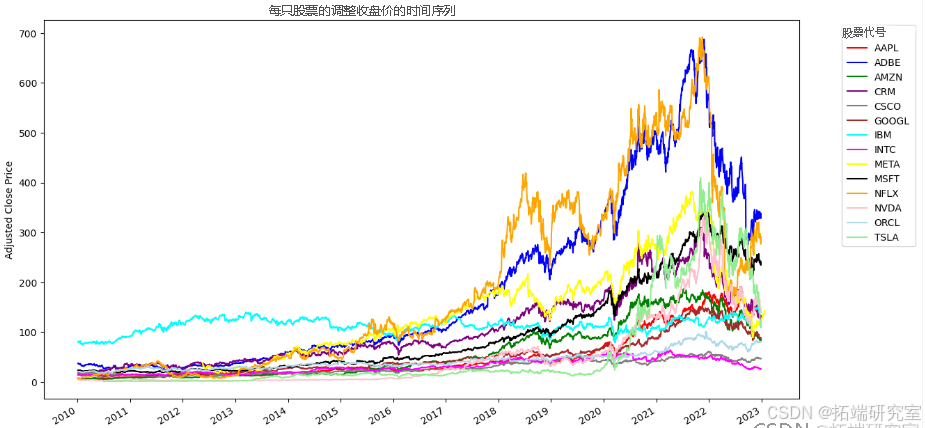
显示 2010 年至 2023 年股票调整后收盘价的时间序列的折线图。每只股票都由一条不同颜色的线表示,股票代码列在右侧的图例中。这些线显示了股价随时间推移的波动,一些股票显示出显着的增长
探索性数据分析
缺失值
数据集中没有缺失值。('stock_symbol'、'date'、'open'、'high'、'low'、'close'、'adj_close'、'volume')中的每一列都有等于条目总数的非空计数,即 45,088。因此,每列的缺失值百分比为 0.0%,确认数据集是完整的,没有缺失数据。

对图
配对图是一个图表网格,显示每个股票变量(如开盘价和收盘价)与其他变量的关系。对角线上是直方图,显示每个变量出现不同值的频率。对角线的散点图显示了两个变量之间的趋势或模式,例如整个数据中最高价和最低价的比较情况。
numerical_data = stock[['open', 'high', 'low', 'close', 'adj_close', 'volume']]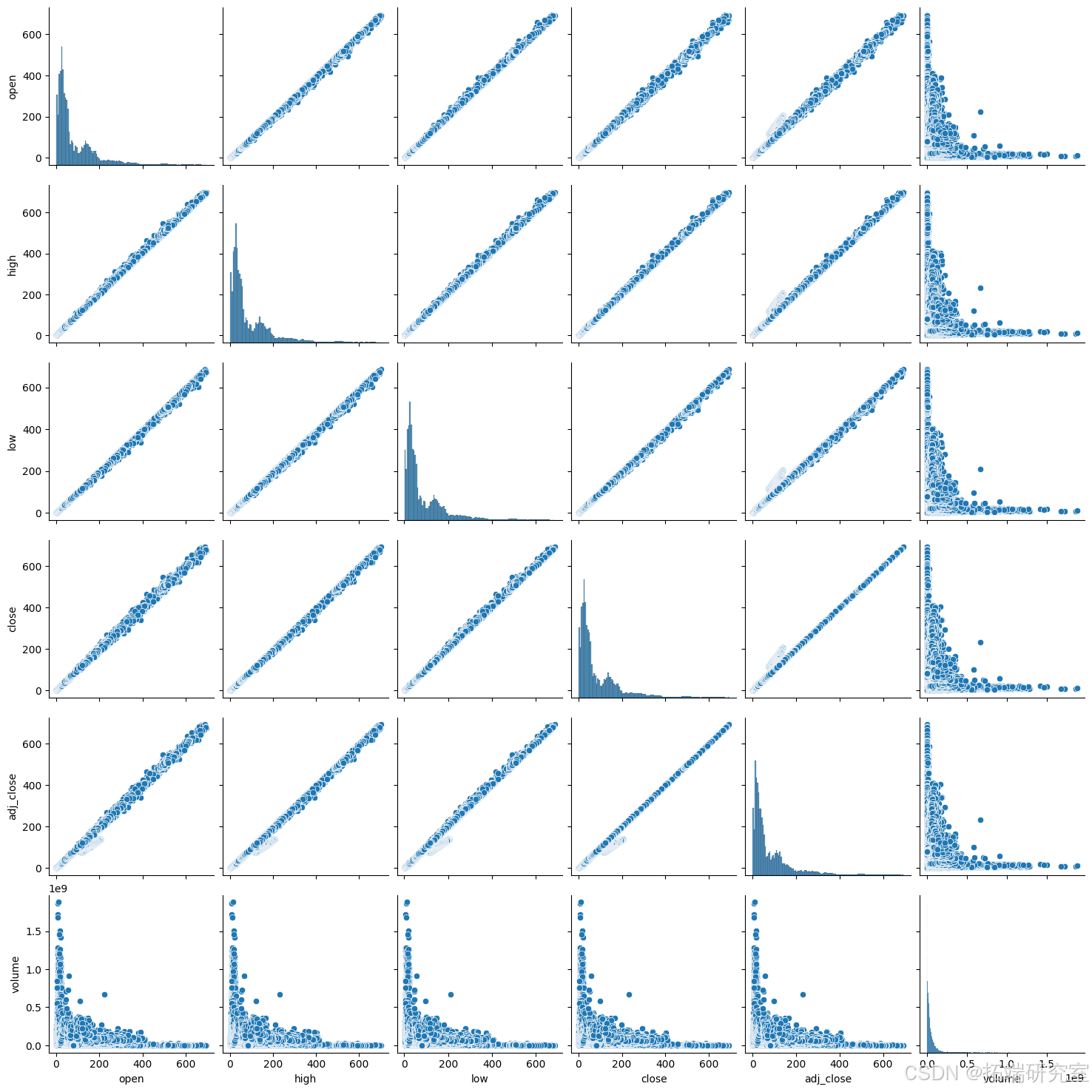
相关热图
热图显示了不同股票市场变量之间的密切关系,例如开盘价和收盘价。深绿色方块表示非常强的关系,开盘价、最高价、最低价、收盘价和调整后的收盘价都是如此,它们都非常相似。成交量与这些价格的关系不大,如棕色方块所示。
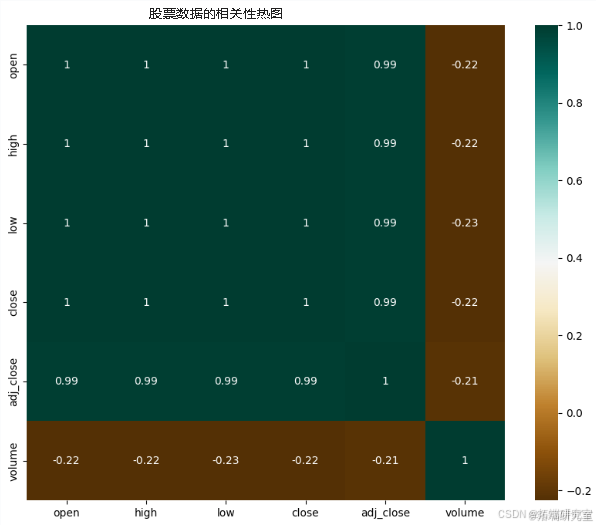
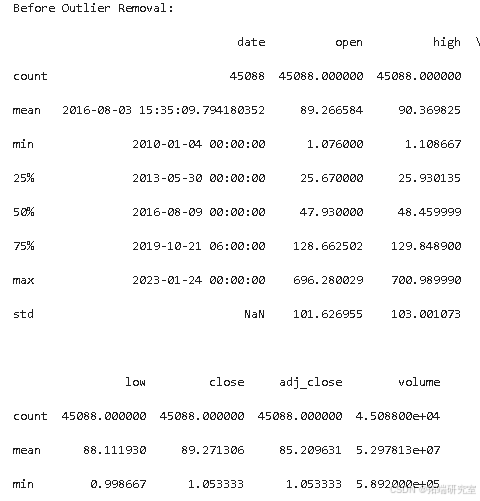
异常
数据集中的异常值可以在每个数值股票列的箱线图中发现,例如开盘价、最高价、最低价、收盘价和调整后的收盘价,以及成交量。描述性统计量显示的值远高于或低于平均值,表明这些是异常值。
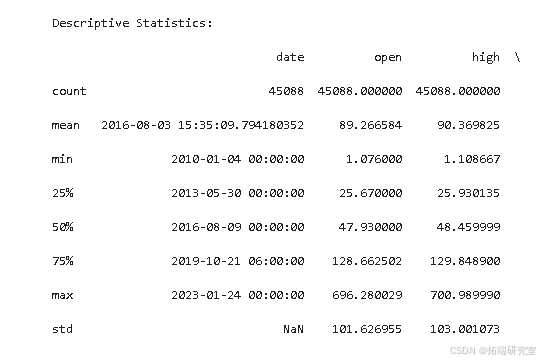





数据预处理
数据清理
由于没有缺失值,因此我们不会执行任何插补技术,如均值或中位数插补或基于模型的方法,也不会删除具有缺失值的行/列。
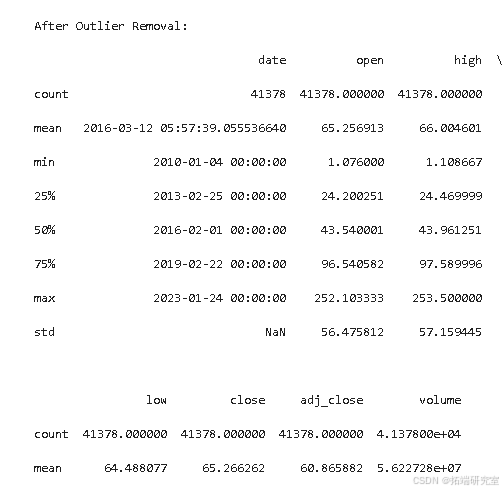
删除异常值
stock_cleaned = remove_outliers(stock, columns_to_check, z_score_threshold)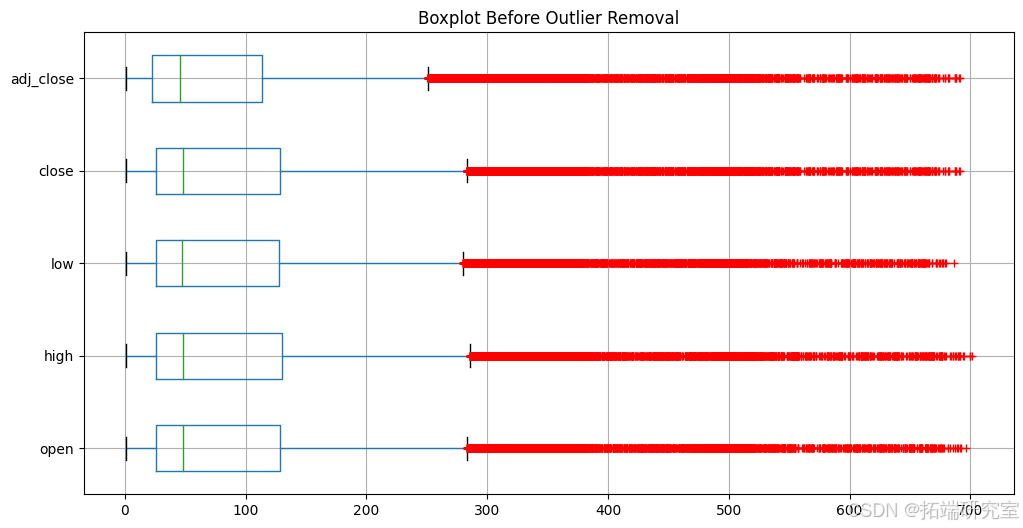
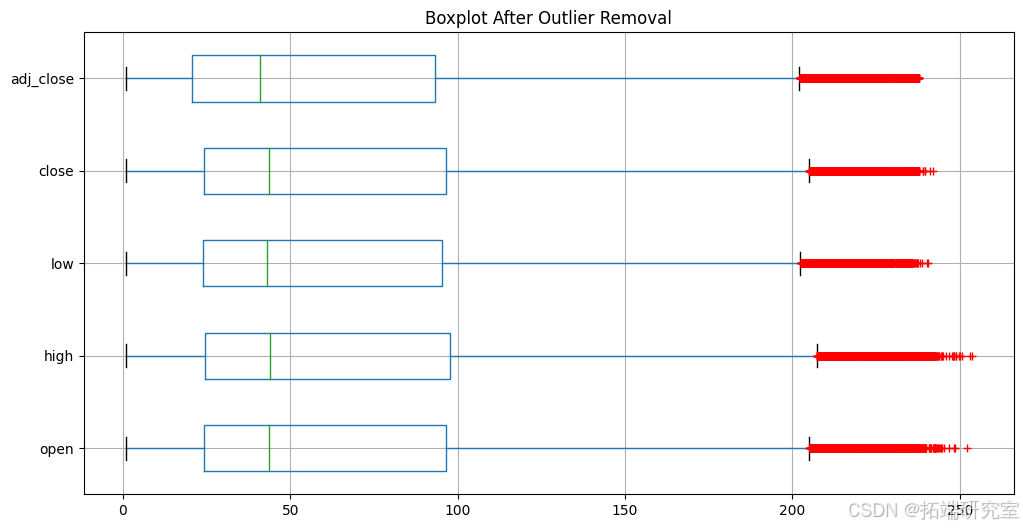
预测分析
对于我们的预测分析,我们开发了一种综合方法,利用四种不同的机器学习模型,每种模型都因其在预测结果方面的独特优势和能力而被选中。这些模型包括:
- 线性回归:评估自变量和因变量之间线性关系的基础模型。
- 套索回归:线性回归的扩展,包含 L1 正则化,有助于特征选择和减少过拟合。
- 随机森林回归:一种集成学习方法,它使用多个决策树,通过平均结果来生成更准确、更稳健的预测。
- 多层感知器 (MLP):一类前馈人工神经网络,可以对输入和输出之间的复杂非线性关系进行建模。
通过利用这些模型的多种方法,我们旨在提高预测分析的准确性和可靠性。
线性回归
在线性回归代码中,我们使用一个模型来预测基于其他市场因素(“开盘价”、“最高价”、“最低价”、“收盘价”)的股价(“adj_close”)。该模型使用部分数据进行训练,然后进行测试以查看其预测新数据的程度,表明它通常准确,均方误差为 92.29,R 平方约为 96.8%。最后,我们用图查看预测价格和实际价格之间的差异,注意模型在哪些方面没有完美预测。
model = LinearRegression()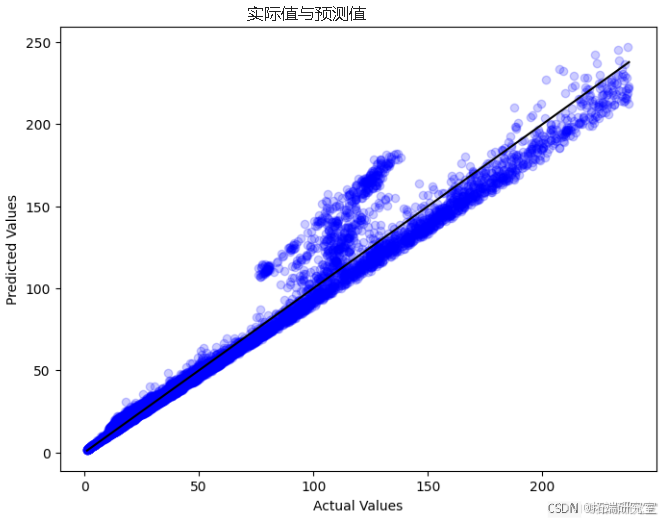
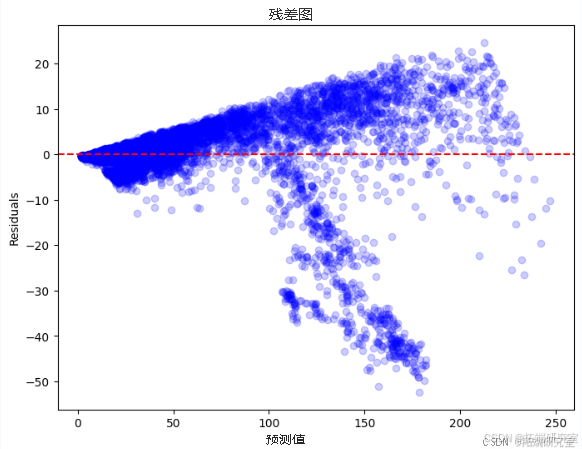
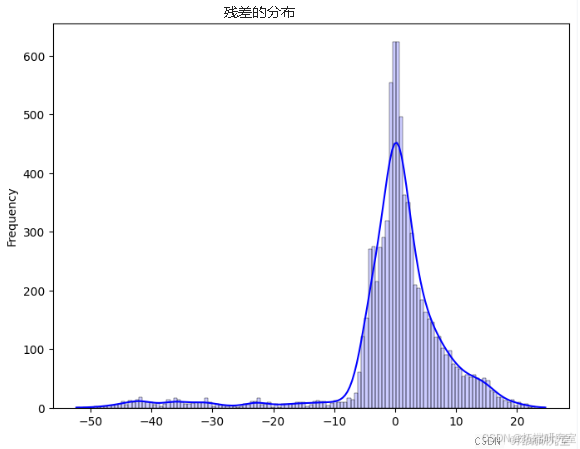
第一张图显示了预测的股票价格与实际价格的比较情况,大多数点位于一条线上,表明预测准确性良好。第二张图显示残差,即实际值和预测值之间的差值;点分散在零线周围,在预测中显示一些误差。第三张图是一个直方图,它告诉我们不同残差发生的频率,大多数接近于零,这表明许多预测接近实际值。
套索回归
在套索回归代码中,我们创建了一个模型,该模型不仅可以预测股票价格,还可以通过减少变量的数量来简化模型,如果某些变量对预测没有多大帮助(这是通过“alpha”值完成的,它控制着这种简化的强度)。该模型的准确率略低于基本线性回归,R 平方约为 96.82%。然后,我们使用散点图和直方图根据实际价格和误差(残差)检查预测。
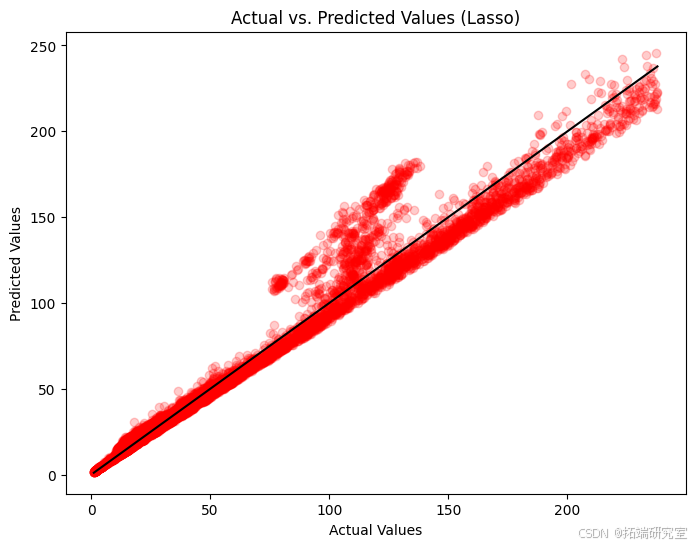
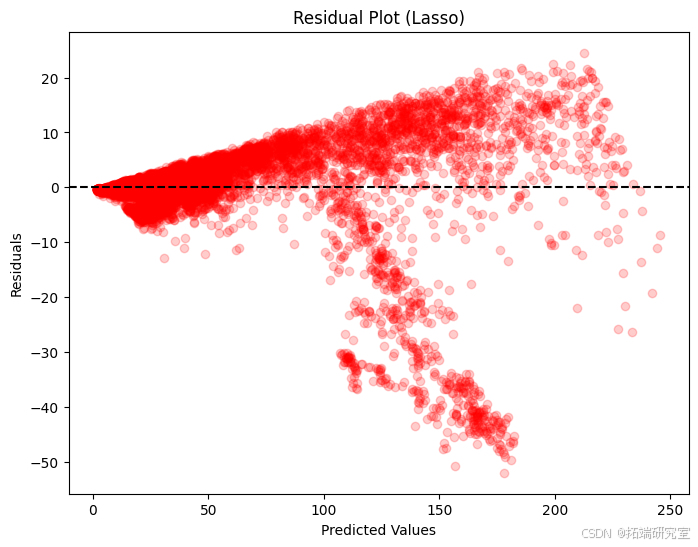

第一张图将实际股票价值与 Lasso 模型预测的股票价值进行了比较,显示了沿线的紧密聚类,表明预测良好,但存在一些价差。第二张残差图显示了预测值和实际值之间的差异,点集中在零线附近,但对于较高的值,则存在一些较大的偏差。第三张图显示了这些差异的分布,主要以零为中心,这表明预测通常接近实际值,尽管有一些明显的例外。
随机森林回归
在随机森林模型代码中,我们使用一组决策树来预测股票价格,与单个决策树相比,这通常会导致更准确和稳定的预测。该模型显示均方误差为 75.59,R 平方误差为 97.4%,表明其预测与实际值非常接近。我们使用绘图直观地将预测值与实际值进行比较,并分析预测误差(残差)。
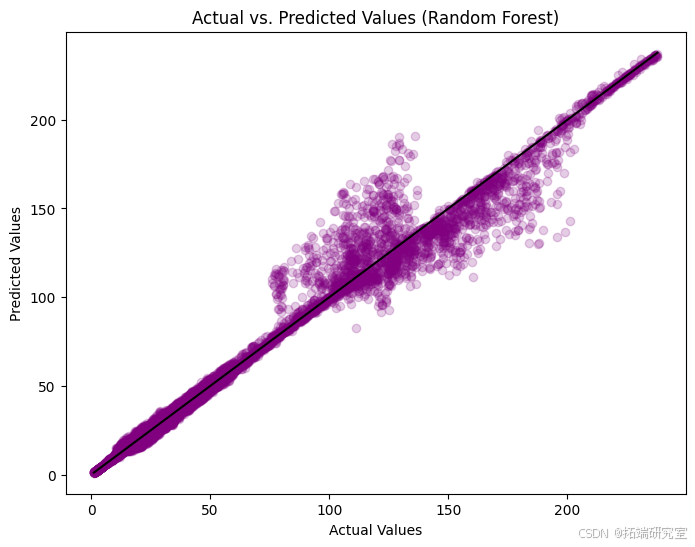
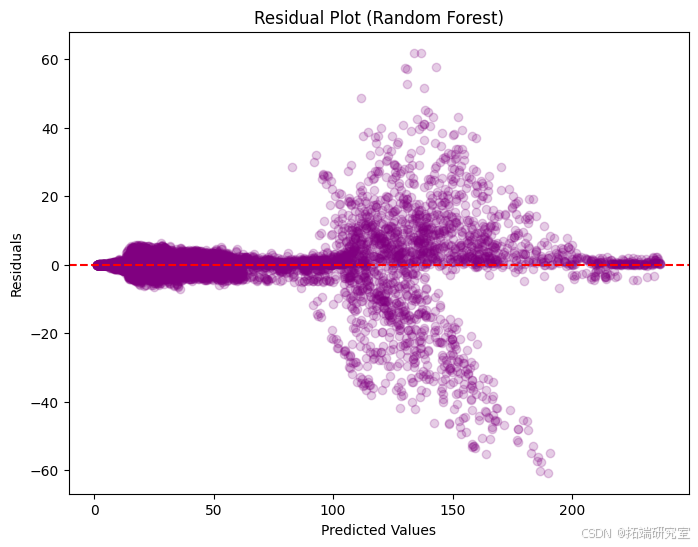
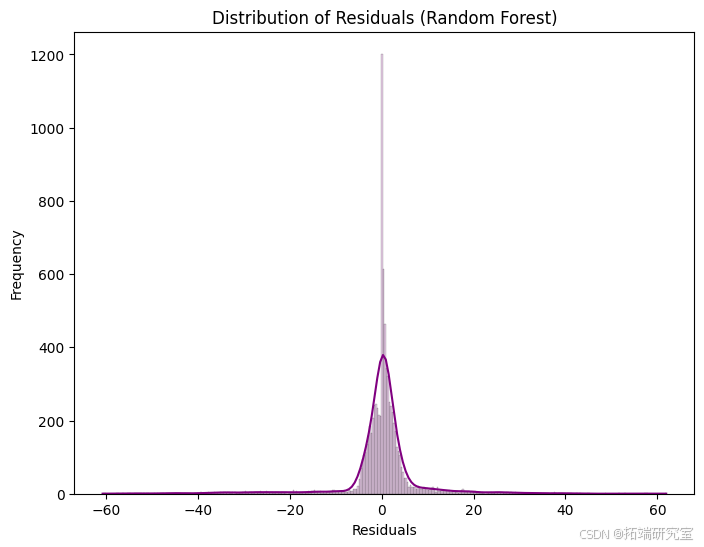
第一张图显示了随机森林模型的实际股价与预测股价,大多数点都接近黑线,表示预测准确。第二张图显示了残差,即预测值和实际值之间的差异,散布在水平线周围,对于较高的值,存在一组较大的误差。第三张图是残差直方图,显示大多数预测都非常准确,峰值在零附近,但也有一些更大的误差离零更远。
多层感知器 (MLP)
在多层感知器模型代码中,我们使用一种具有两层处理的神经网络来预测股票价格,网络通过其层“学习”复杂的模式。该模型的均方误差约为 97,R 平方得分约为 96.7%,这意味着它非常擅长做出与实际数据相匹配的预测。我们使用几个图来检查预测值与实际值的比较情况,并查看预测误差,即残差。
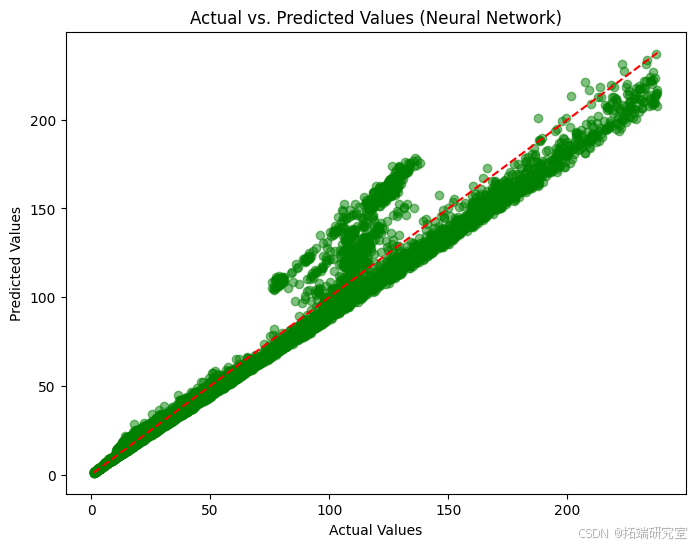
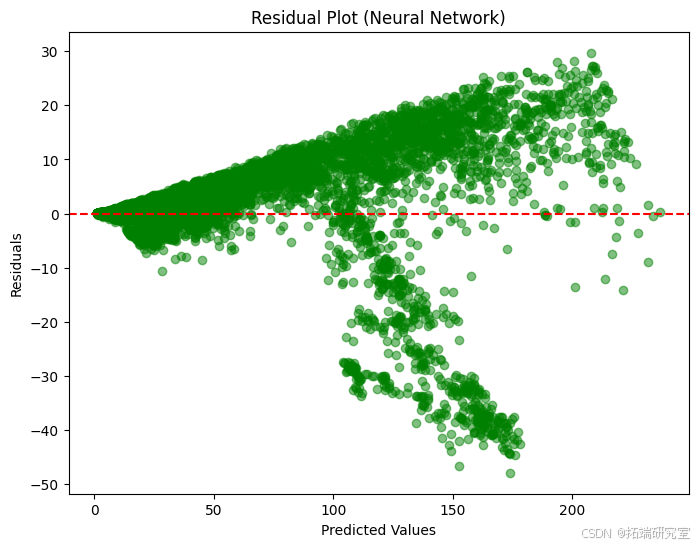
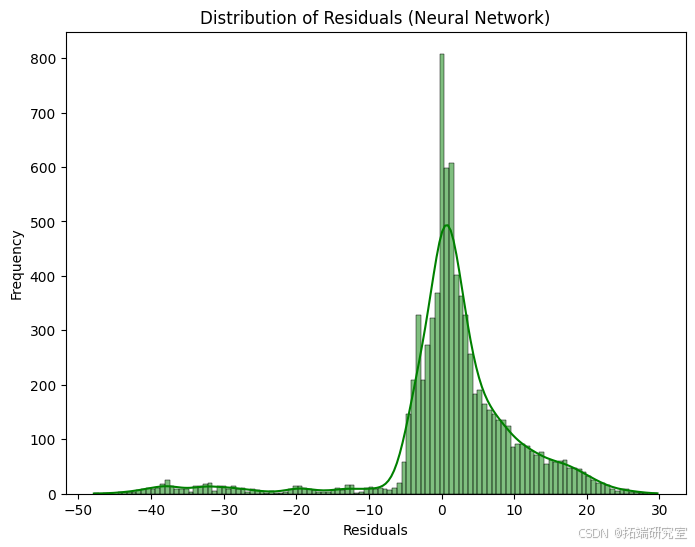
第一张图显示了神经网络模型对实际和预测股票价值的比较,主要是沿着这条线,这意味着预测是好的。第二个图是一个残差图,它显示了预测中的一些误差,特别是对于较高的值,因为它们偏离了零线。第三张图是一个直方图,在零附近急剧达到峰值,表明大多数预测接近实际值,但也有一些误差离零更远。
使用 ARIMA 模型进行时间序列预测
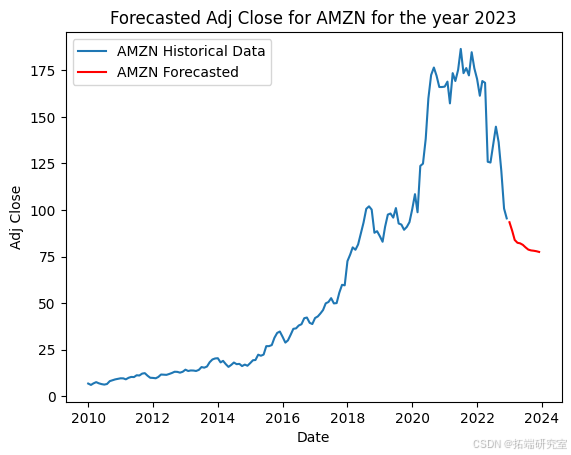
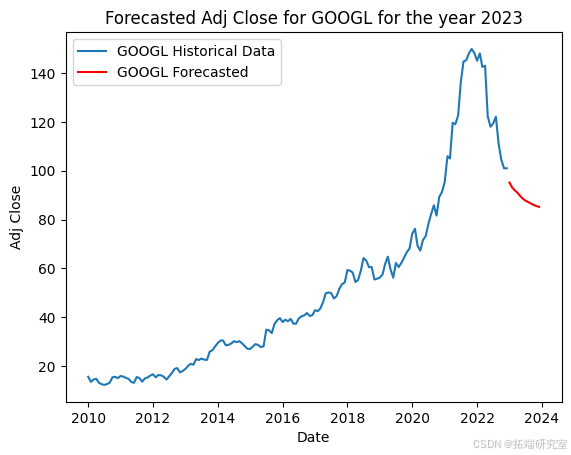
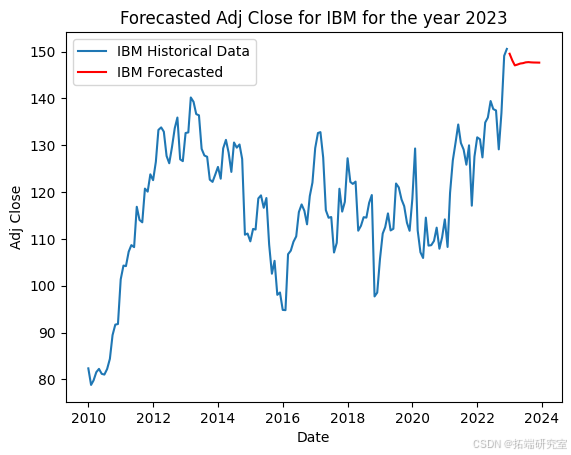
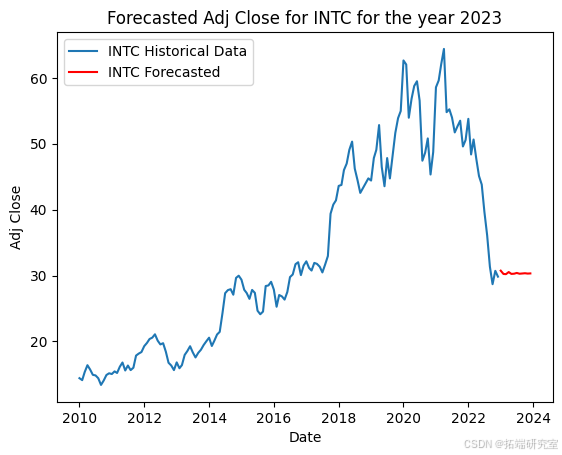
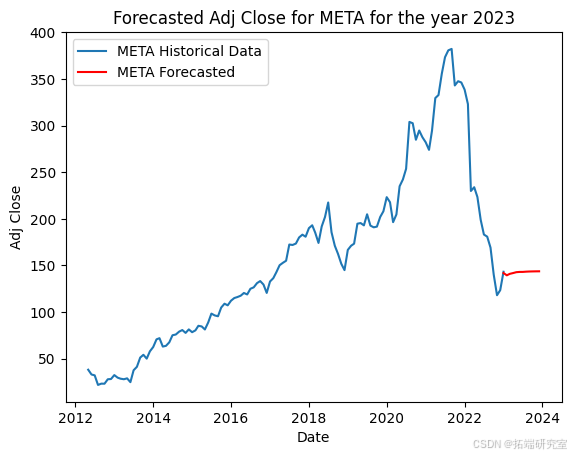
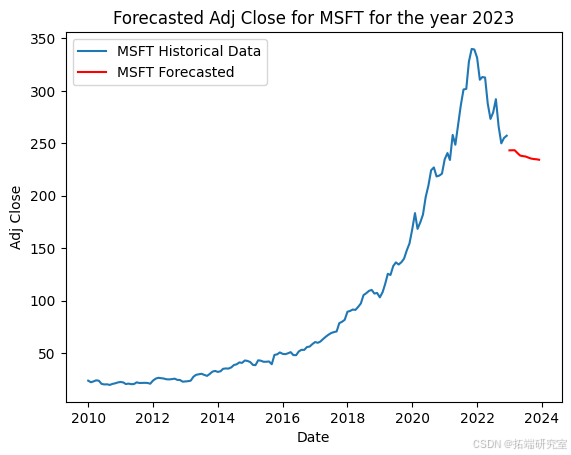
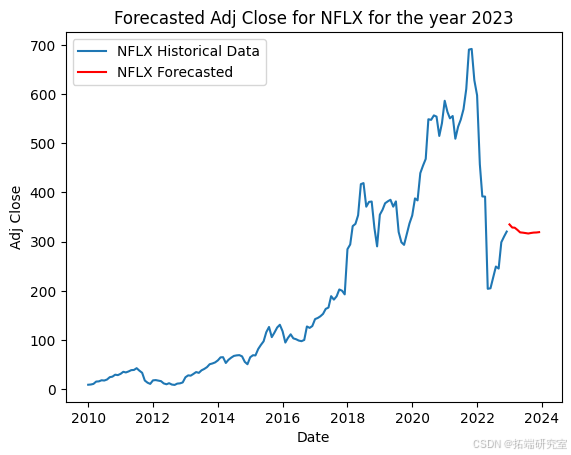
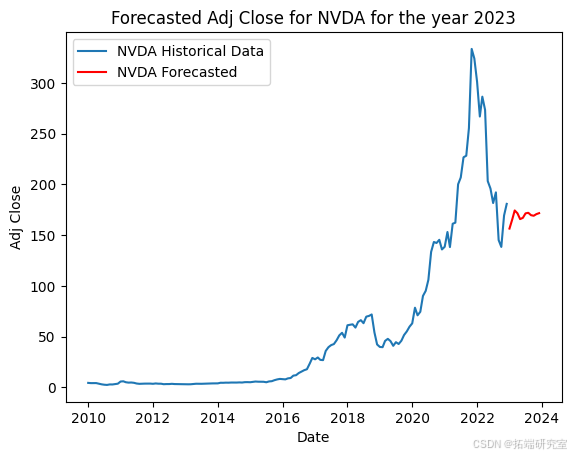
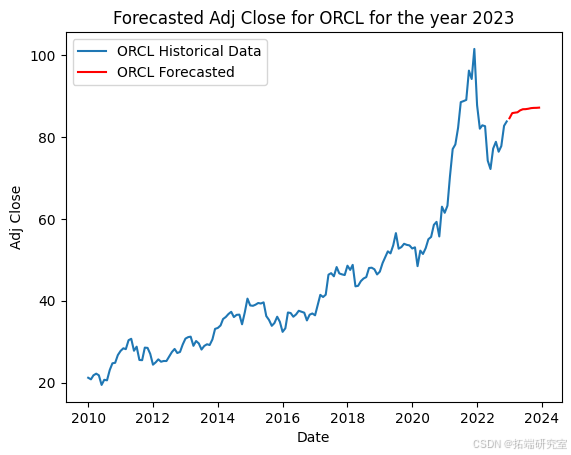
该代码准备股票市场数据,并使用 ARIMA 模型预测每只股票的未来调整后收盘价。首先,它将 2023 年初之前的历史数据分开以训练模型。然后,它按日期和股票代码对数据进行分组,选择每个月的最大调整收盘价。对于每只股票,它都会根据历史数据拟合 ARIMA 模型,并使用它来预测 2023 年未来 12 个月的收盘价,并在历史数据旁边用图表显示这些预测。
model = ARIMA(dataf_max_pivot[symbol], order=(5,1,0))
model_fit = model.fit()
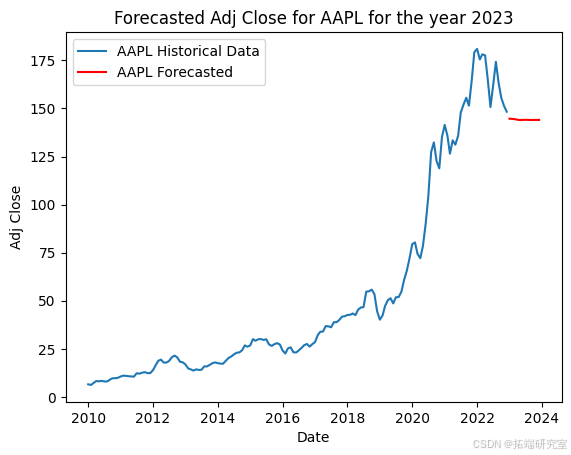
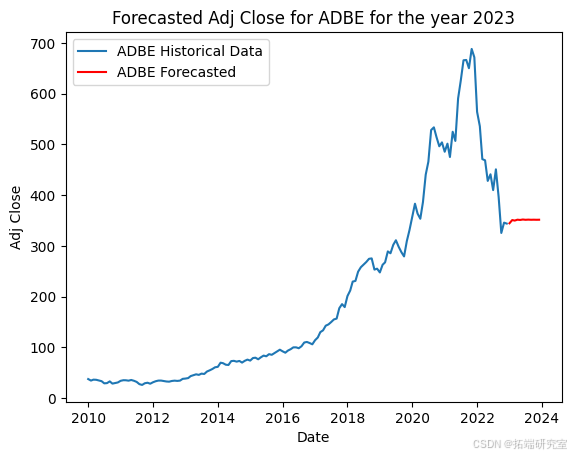



关于分析师
在此对Haopeng Li对本文所作的贡献表示诚挚感谢,她在上海财经大学完成了控制工程专业的硕士学位,专注人工智能领域。擅长Python、Matlab仿真、视觉处理、神经网络、数据分析 。