数据分析学习记录（二）—响应曲面法及Design-Expert的简单使用

注：本文参考博客链接：https://www.biomart.cn/experiment/793/2714853.htm

一 引言

响应曲面法（Response surface methodology）在百度百科上的解释：

“响应曲面法是优化随机过程的统计学试验方法。目标是寻找试验指标与各因子间的定量规律，找出各因子水平的最佳组合。在多元线性回归的基础上主动收集数据，以获得具有较好性质的回归方程。建立的复杂多维空间曲面较接近实际情况，所需要的试验组数相对较少，在模拟和系统动力学中得到广泛应用。”

对于我来说怎么样去更简单直观的理解它是我在自学时首要考虑的问题。第一点，我们为什么需要使用响应曲面法？这里就要引出另一个最常用的过程优化方法，单因素试验。

单因素试验是假设各因素间不存在交互作用的前提下，每次只改变一个因素，其他因素需要保持在恒定水平下，再去研究不同试验水平对响应值的影响。

而在实际情况中过程影响因素十分复杂，并且因素与因素之间通常都会存在一定的交互作用，当试验因素很多的时候，我们需要进行数次的单因素分析以及较长的试验周期才能逐个优化各因素，这样效率未必太低。

此时又不得不提到一个效率比单因素分析更高的过程优化方法，那就是正交试验。正交试验可以同时考虑多因素，在合理减少单因素分析的试验次数的情况下，寻找最佳的因素水平组合，通过方差分析得到影响结果的主次因素，但正交试验在处理因素间交互作用时需要设计交互作用表，当因素间的交互更为复杂时，正交试验的工作量也会随之上升。

于是。。

响应曲面法应运而生。 响应曲面法又叫回归设计，其实了解过响应曲面法的分析原理后对于它这个名字就不难理解了，它在多元线性回归的基础上建立一个包括各显著因素的一次项、二次项和任何两个因素之间的一级交互作用项，可以说是集统计、数学和计算机与一体的统计学范畴的过程优化方法。

响应曲面法通过设计合理的少次数的试验，精确研究各因素和我们想得到的响应值之间的关系，快速有效的确定多因素系统的最佳条件。

二 实例

这里我找了一篇文献，用其中的数据分析结合Design-expert软件进行响应曲面分析。响应面常用的方法有两种：中心复合试验设计（central composite design，CCD）和 Box-Behnken 试验设计（BBD）。

常用的响应面设计和分析软件有 Matlab、SAS 和 Design-Expert。在已经发表的有关响应面（RSM）优化试验的论文中，Design-Expert 是使用最广泛的软件。

参考文献信息：
[1]胡栋, 柯灵超, 张敬宇,等. 响应面法设计优化阿维菌素化学合成发酵培养基[J]. 中国抗生素杂志, 2018, 043(008):1055-1061.

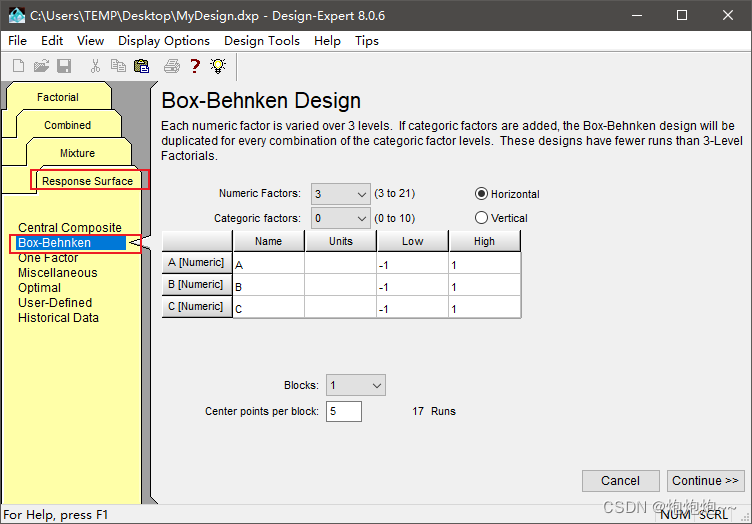
首先打开软件，选择新建分析，然后选择响应曲面分析，选择第二个Box-Behnken ，如图：

我们对照文献中的数据表填写，输入对应的因素数量以及试验中的绝对因素（默认为0），然后输入因素的名称单位、最大值和最小值，点击continue进入下一个页面：

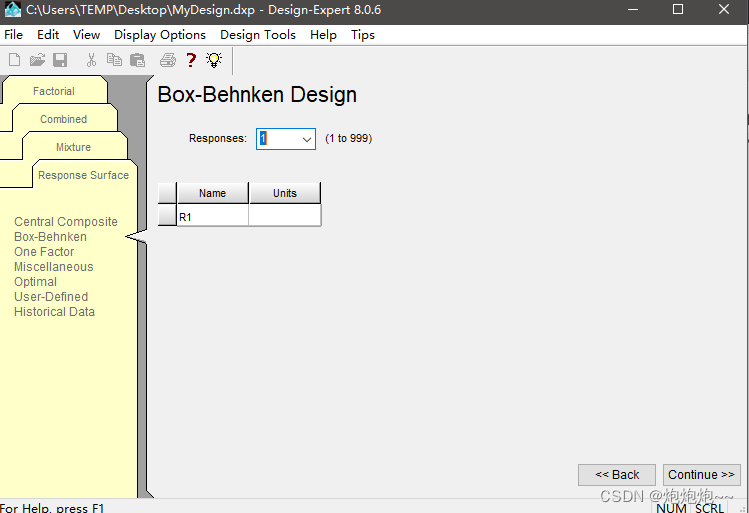
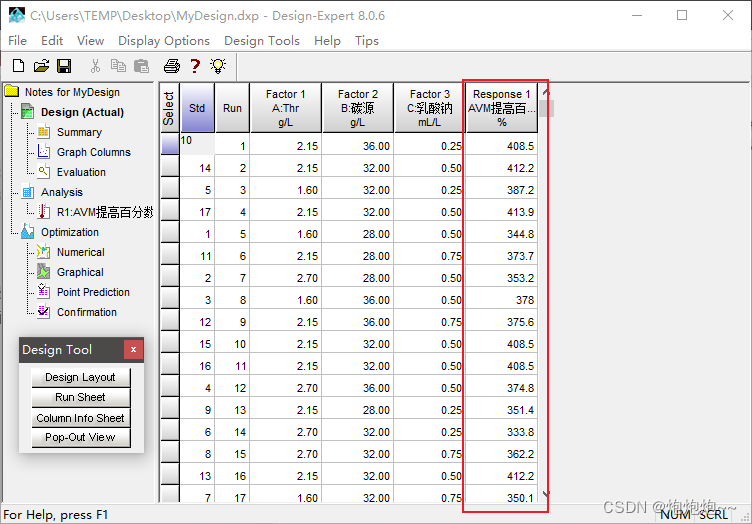
在这里填写对应我们想优化的响应值，这篇文献中只有 一个响应值，为阿维菌素提高百分数，于是我们填写进去，单位为**%**，点击continue：

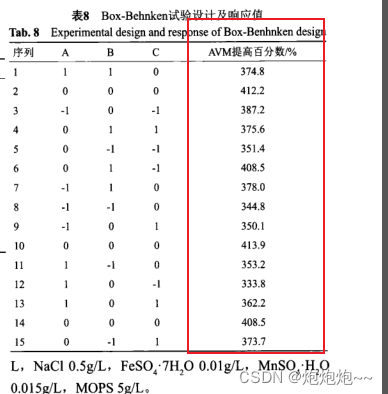
如上图的表后面的响应值数据是需要手动输入进去的，对应上面那一张表里的数据。
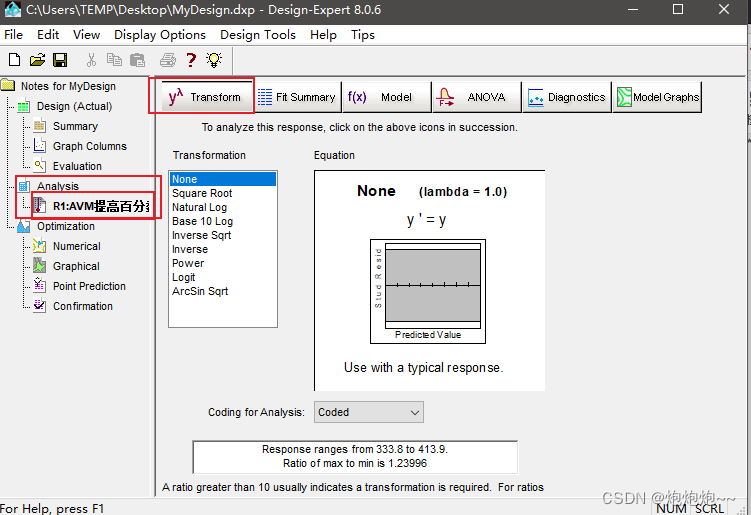
输入好之后我们点击Analysis的R1：Transform 选项卡，一般选择默认值即可。如果有别的要求，可以根据需要和指示查找每种模式的详细介绍再选择。

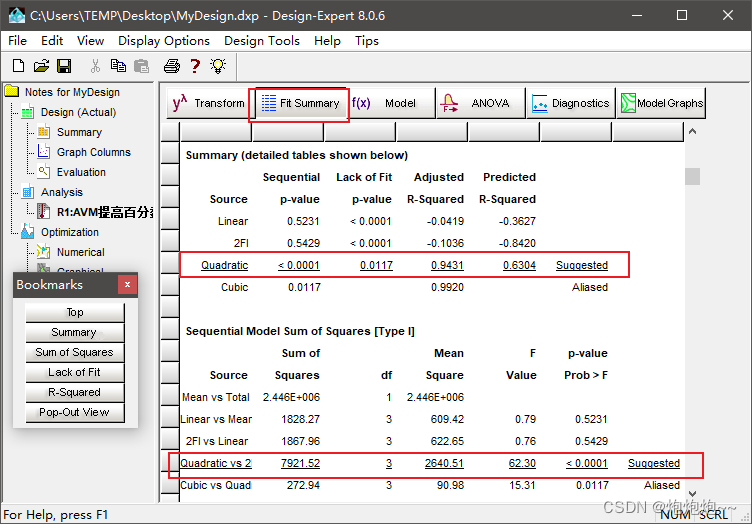
FitSummary，可以看下建议的因素。

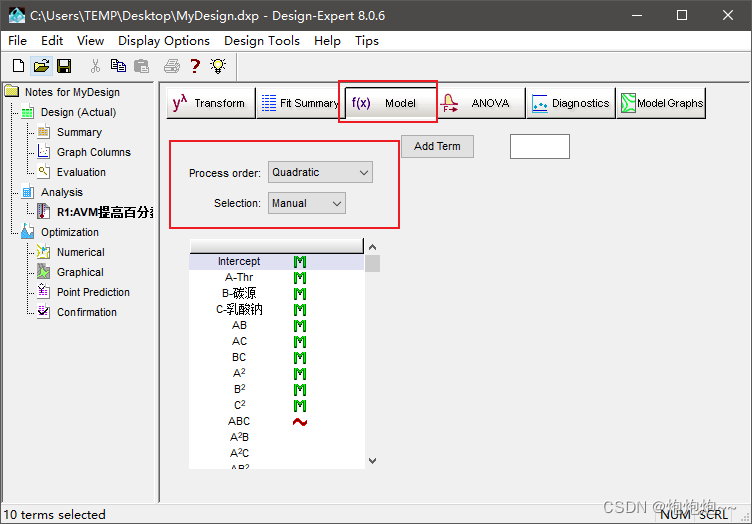
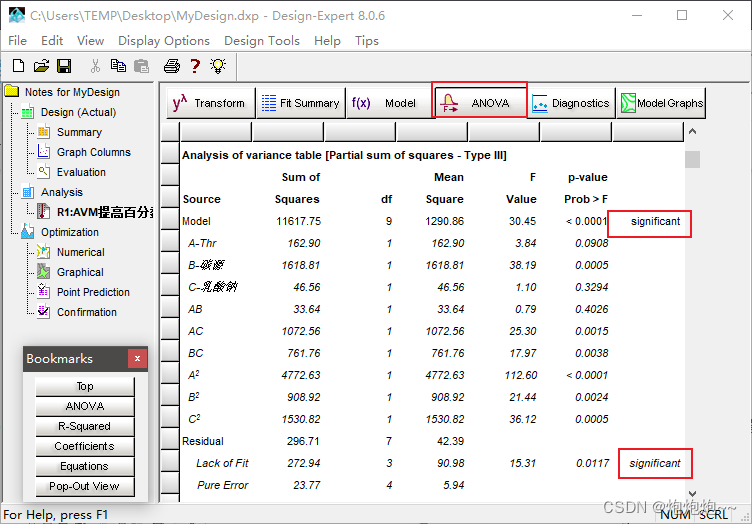
Model 选项卡取默认值即可，点击 ANOVA 选项卡，显示方差分析，方差的显著性检验，系数显著性检验回归方程。

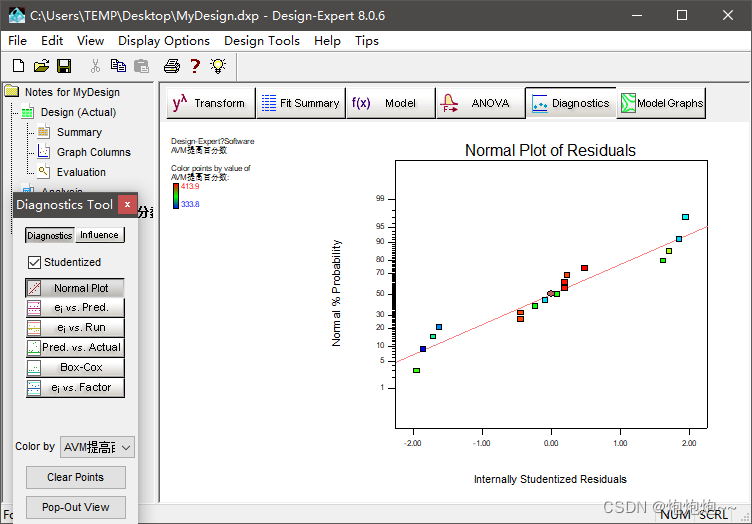
点击 Diagnostics 选项卡，依次点击左端选项，首先展示的是 Normal Plot，参差的正态规律分布图，图中的点越靠近直线越好。

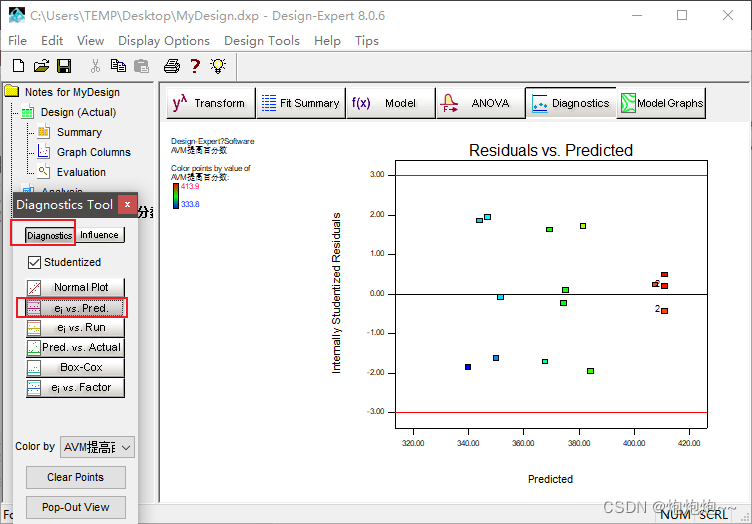
第二个展示残差与方程预测值的对应关系图，分布越分散越无规律越好。

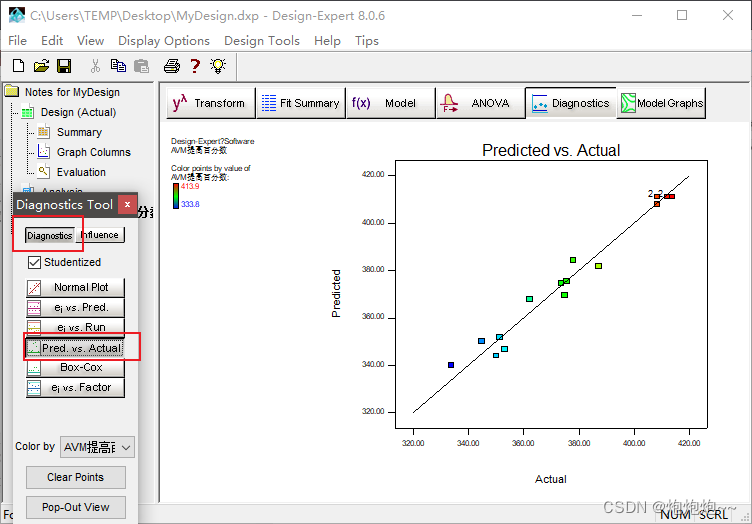
最后展示的是预测值和试验实际值的对应关系图，点越靠近同一条直线越好。

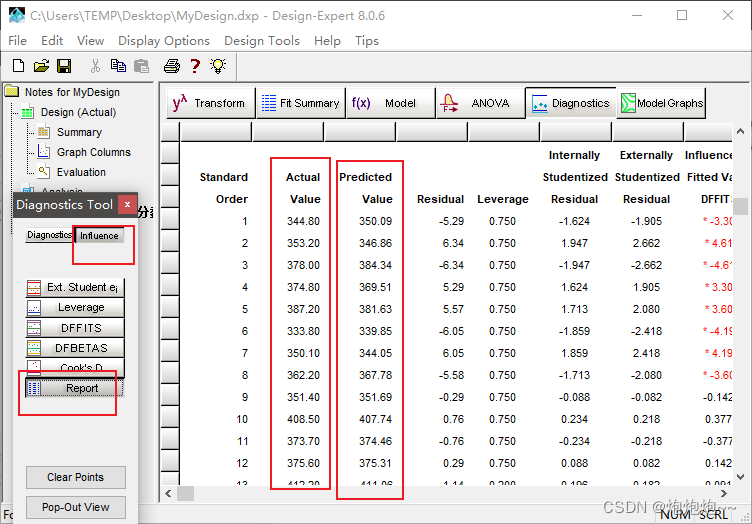
然后点击 Influence 后再点击 Report 进入结果界面，数据显示如图，包含试验实际测量值（左）和方程预测值（右）。

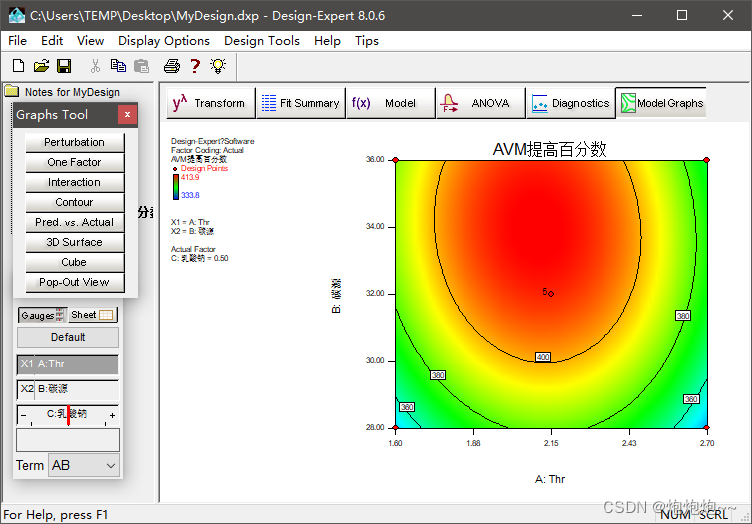
然后点击 Model Graphs 查看等高线图，等高线图考察每两个因素对因变量造成的影响，并由拟合的方程形成等高线，为二维平面图形，可经由该图找出较好的范围。

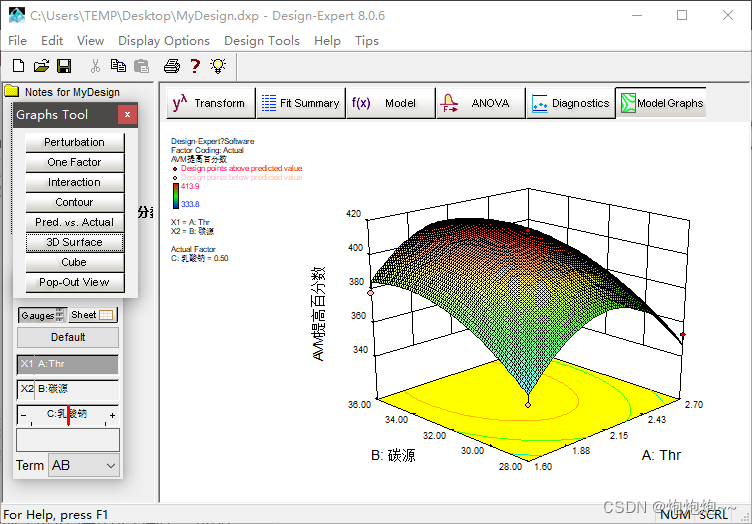
三维响应曲面图可更加直观地看出两因素的影响情况，可以很直观地找出最优范围，刚才所看到的二维等高线图即为三维响应面图在底面的投影图。

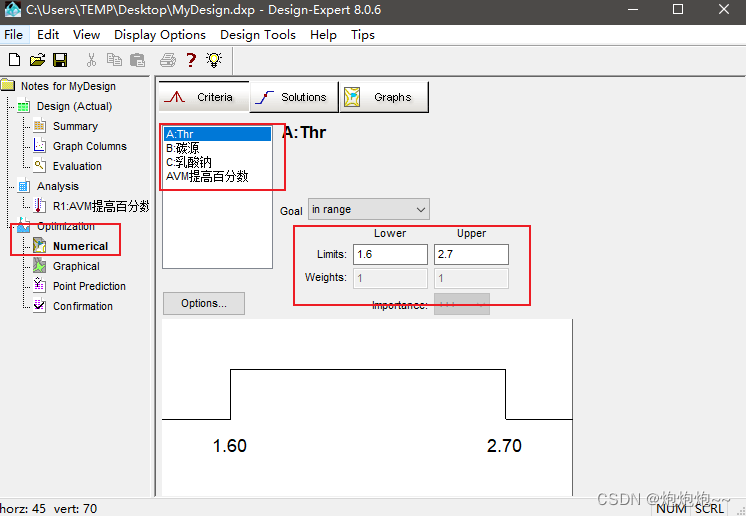
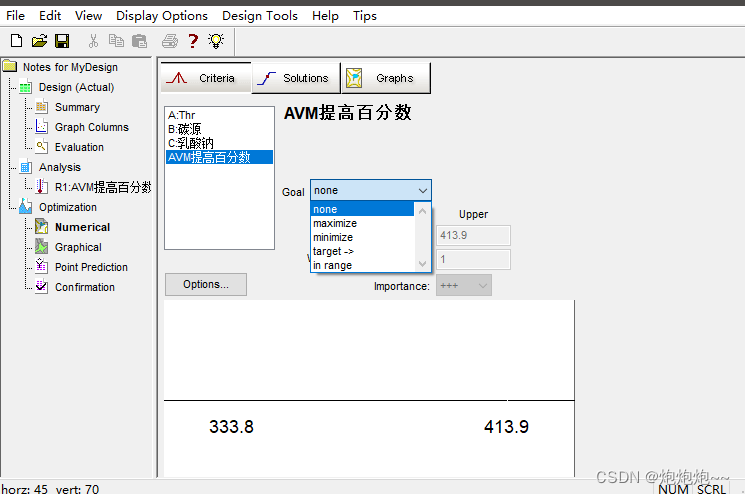
接下来是关键的优化条件选项，根据实际情况确定每个因素可以取值的范围，然后进行「响应值目标」的确定，每个试验都有不同的目的，比如此处我们想要找到能使阿维菌素最大产出量的最优培养条件，但别的试验中对目标的要求有需要最大值，有需要最小值，有时候需要把结果稳定在某个范围或者需要一个固定的数值。那么在这四种模式中就可以选择其相对应的情况。

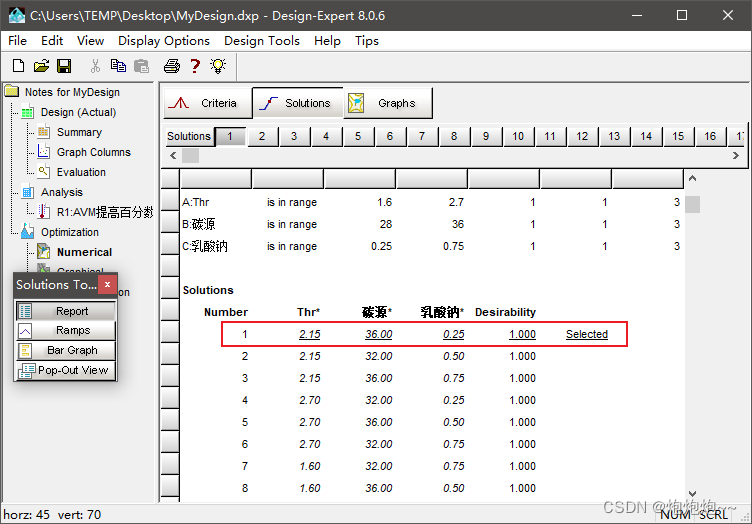
点击 Solutions 选项卡，即可看到经过分析得到的最优值，一般会列出许多方案，第一个方案就是各因素取最优值后的结果可取到的最大化的解决方案，为预测值。

以上！！！若有不对，欢迎交流指出。