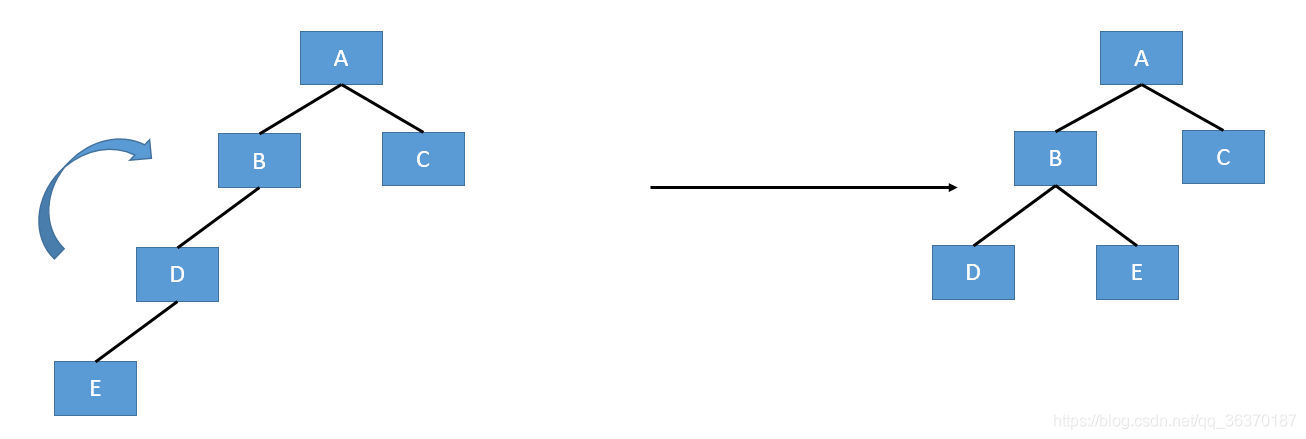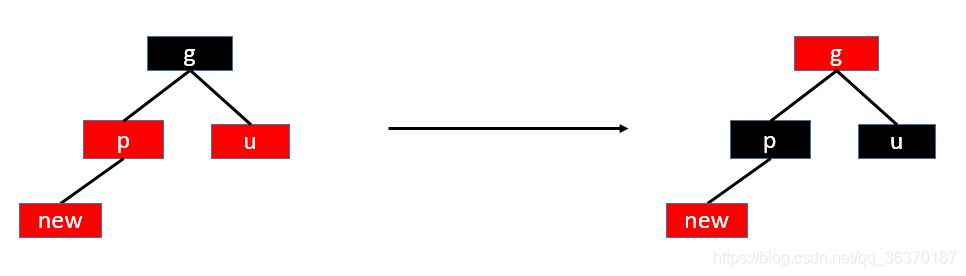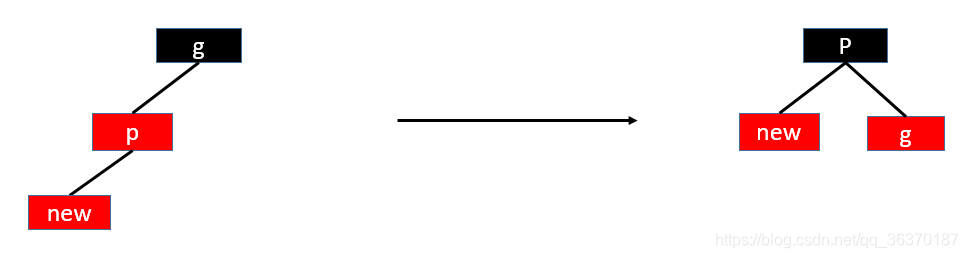二叉平衡树(AVL)
- 各个左右子树长度之差不超过1
- 插入节点之后,如果出现不平衡,那么首先要找到最小不平衡子树
- RR,插入E后,最小不平衡子树是CDE,不平衡出现在C的右节点、D的右节点,所以称为RR,左转即可
- RR,插入E后,最小不平衡子树是BDE,不平衡出现在B的左节点、D的左节点,所以称为LL,右转即可
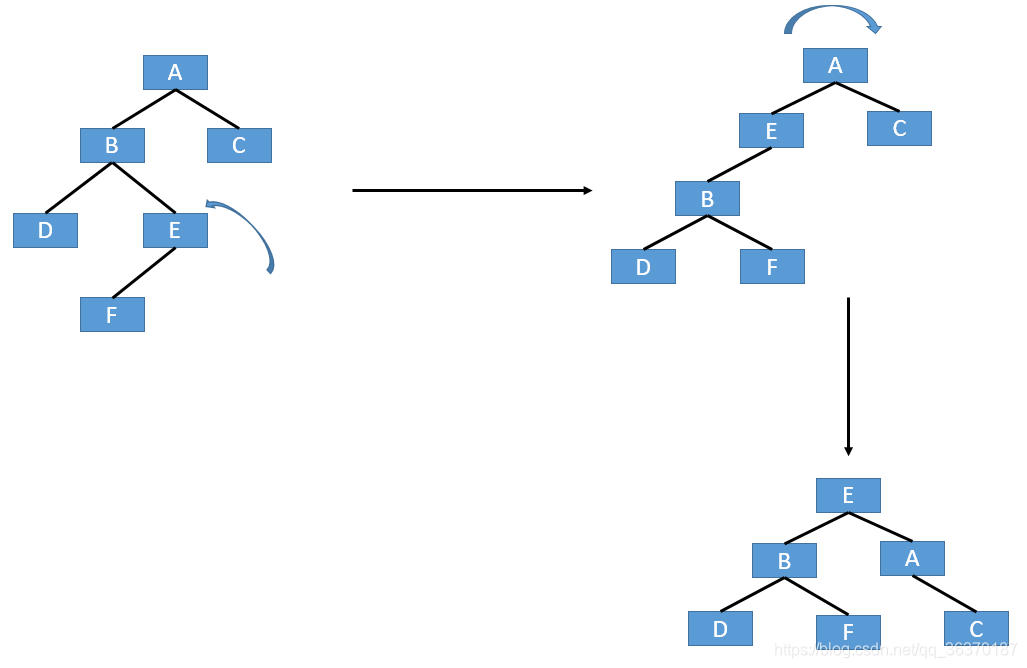
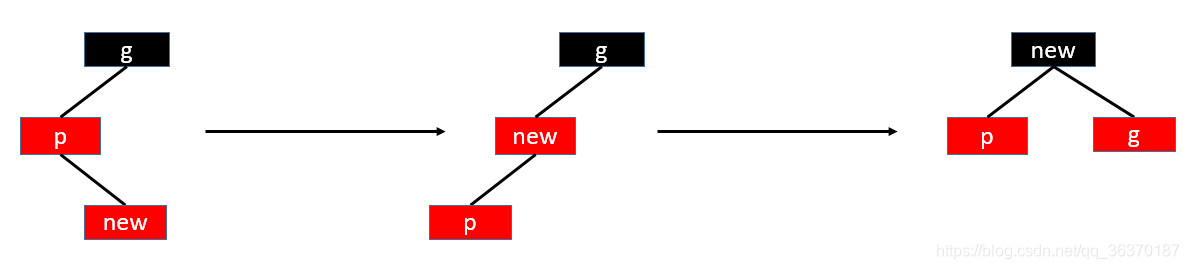
- LR,插入F后,最小不平衡子树是ABCDEF,不平衡节点出现在A的左节点、B的右节点,所以称为LR
- 根据小到大原则,从子树B开始处理,不平衡节点出现在B的右节点,那么左转
- 然后处理A节点,不平衡节点出现A的左节点,那么右转
- 所以处理上,是先左后右,也是LR
- RL,插入F后,最小不平衡子树是ABCDEF,不平衡点出现在A的右节点、C的左节点,所以称为RL
- 根据由小到大原则,处理C节点,不平衡点出现在C的左节点,那么右转
- 然后处理A节点,不平衡点出现在A的右节点,那么左转
- 处理上是先右后左,也是RL
- 还有两种简单的LR和RL,如下
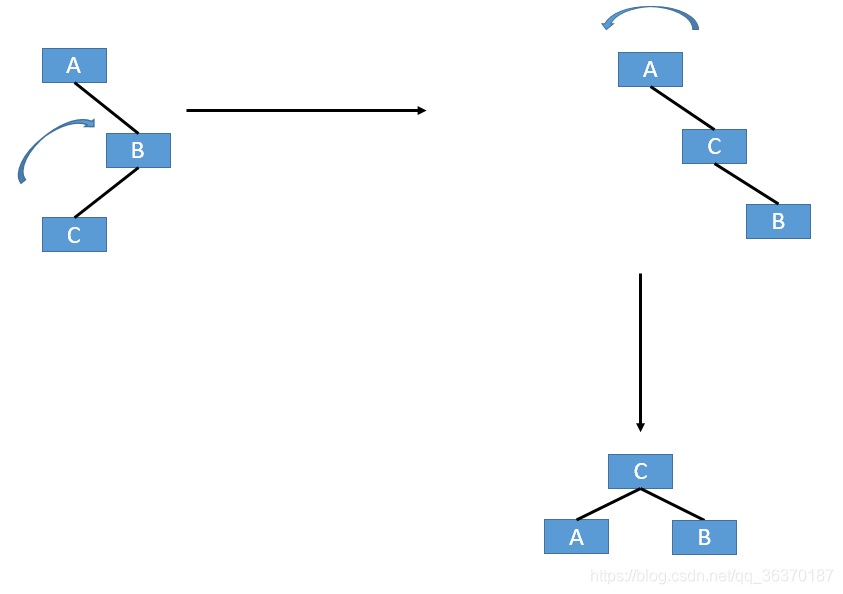
- LR,最小不平衡树出现在ABC,在A的左、B的右,先左转处理BC(小子树),再右转处理ABC(大子树)
- RL,最小不平衡树出现在ABC,在A的右、B的左,先右转处理BC(小子树),再左转处理ABC(大子树)
红黑树
参考:https://www.jianshu.com/p/e136ec79235c
- 自平衡二叉查找树,不像二叉平衡树那样要求严格,所以插入的时候调整的频率没有二叉平衡树高,所以插入效率较快;但是由于红黑树平衡度要求不高,所以查询速度稍逊于平衡二叉树
- 红黑树适合 插入频繁,但是查找不那么频繁的
- 平衡二叉树适合 查找频繁,但是插入不那么频繁的
- 红黑树定义:
- 每个节点要么是黑色,要么是红色
- 根节点要求是黑色(这里的叶子节点和普通的二叉树中的叶子节点不一样,这里的叶子节点指的是原二叉树叶子节点的左右空指针NIL)
- 叶子节点要求是黑色
- 红色节点的孩子节点是黑色的,也就是上下不能同时出现两个红色节点
- 任何一个节点,从其开始到任何一个叶子结点的路径,各个路径包含的黑色节点的数量是一致的,也就是黑色高度(brack height,bh)一样
- 红黑树的高度,不超过
,所以查询效率虽然没有平衡二叉好,但还是在一个数量级
- 定义4确保了,最短的路径上只有黑色节点,最长的路径上黑色和红色节点交替出现
- 定义5确保了,每条路径黑色节点数量一致,那么最长的长度,就是红黑交替,那么最多也就两倍黑色长度那么长,所以是
- 红黑树自平衡三种操作:左旋、右旋、变色
- 刚插入的时候,都是先红色,如果不满足定义的要求(平衡要求),就需要旋转、变色调整了
- 插入1:红黑树为空,直接插入点作为根节点,然后调整颜色为黑色
- 插入2:插入节点已存在(value一样),那么更新值
- 插入3:插入节点的父节点是黑色,那么直接插入即可,不需要自平衡
- 插入4:插入节点的父节点为红色,那么该插入节点一定存在祖父节点,因为红色节点不能作为根节点
- 插入4.1:插入节点的叔叔节点存在且为红色,那么需要如下操作:
- 将祖父节点g设置为红色
- 父亲p和叔叔u节点设置为黑色
- 如果祖父节点g的父节点为黑色,那么搞定,不用处理了;如果祖父节点g的父节点是红色,那么将其当做新插入点,重新执行4.1知道满足条件(肯定会满足,因为根节点是黑色)
- 插入4.2:插入节点不存在叔叔节点或者叔叔节点时黑色,并且插入结点的父亲结点是祖父结点的左子结点
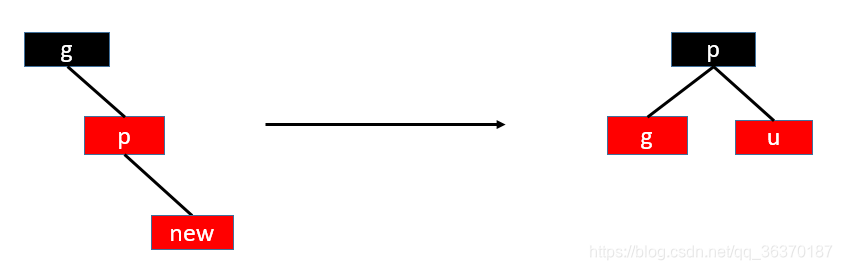
- 插入4.2.1:插入节点是其父节点的左子节点,那么需要如下操作:
- 祖父节点g变红
- 父节点p变黑
- 右旋转
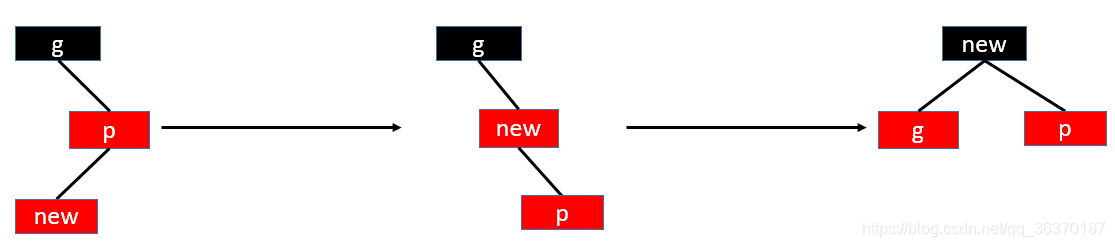
- 4.2.2:插入节点是其父节点的右子节点,那么需要如下操作:
- 父节点p和插入节点new左旋
- 将父节点p和插入节点new互换身份,这样子就变成4.2.1的情况啦
- 按照4.2.1处理就好啦(4.2中已经默认了要么叔叔不存在,要目叔叔是黑色节点,当叔叔不存在的时候,就是下面这样情况;当叔叔存在,叔叔是黑色的,还是当祖父g的子节点也满足呀)
- 4.3:插入节点不存在叔叔节点或者叔叔节点时黑色(该条件和4.2一致),并且插入节点的父节点是祖父节点的右节点(和4.2不同的就是父节点是祖父节点的左节点,这个和4.2对称)
- 4.3.1:插入节点是其父节点的右子节点,那么需要如下操作:
- 将父节点p变为黑色
- 将祖父节点g变为红色
- 对父节点p和插入节点new进行左旋操作
- 4.3.2:插入节点时其父节点的左节点,那么需要如下操作:
- 将p和new进行右旋
- 将new和p对换角色,这样子就变成4.3.1的情况了
- 按照4.3.1的情况来处理就好了
- 删除后需要自平衡,分为以下情况:
2-3树
- 每个节点都有2个或者3个孩子
- 一个2节点包含1个元素和2个孩子(或者没有孩子)
- 一个3节点包含2个元素和3个孩子(或者没有孩子)
- 2-3树所有的叶子节点都在同一层
- 插入分为三种情况:
- 插入情况1:对于空树,直接插入即可,变为2节点
- 插入情况2:插入到2节点中,直接变成3节点
- 插入情况3:插入到3节点中,需要将3节点拆除,然后将3节点中的两个元素或者新插入的元素向上挪一层
- 插入情况3-1:插入的3节点的父节点是2节点:插入的6、7节点是3节点,其父节点4是2节点
- 插入5,将6、7节点拆分,然后将6放到4中,5和7个作为一个2节点
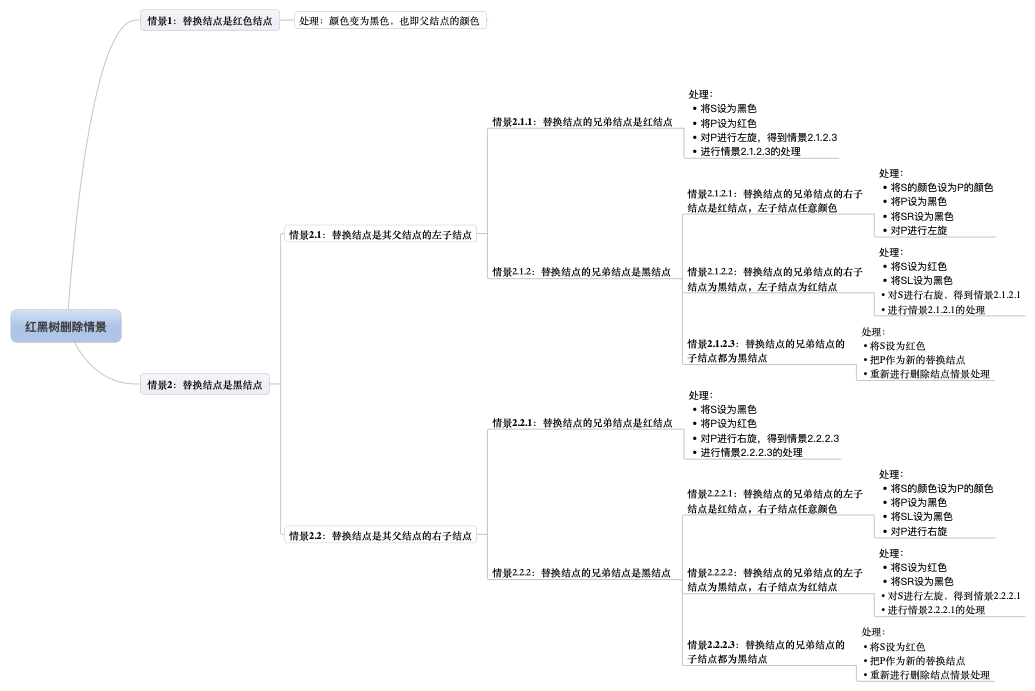
- 插入情况3-2:插入的3节点的父节点是3节点:插入11,插入的9、10是3节点,其父节点12、14也是3节点,其曾祖节点8是2节点,所以想到其曾祖节点可以操作
- 将9、10节点拆分,将9、10、11中的10往上放;
- 将12、14节点拆分,将10、12、14中的12往上放
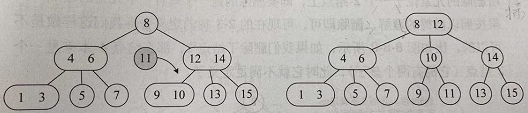
- 其实插入,总结来看就是,不断的将不满足的节点拆分,然后将多出的元素往上挪,那这样会有一个情况,就是挪到最后根节点也是3节点,那么这个时候只能拆掉根节点,整个树增加一层,高度+1了,比如下面的例子:
- 先拆1、3节点,将1、2、3中的2往上挪
- 然后拆4、6节点,将2、4、6中的4往上挪
- 最后到根节点了,拥有4、8、12元素,那么这个时候不能往上挪了,只能拆分根节点然后往下增加高度了
2-3-4树
- 4节点,要么有4个孩子,要么没有
- 3节点,要么有3个孩子,要么没有
- 2节点,要么有2个孩子,要么没有
B树(多路查找树)
- 2-3树和2-3-4树是B树的特例
- B树中最大的孩子数目称为B树的阶,m阶B树具有如下属性:
- 如果根节点不是叶节点,那么至少有两颗子树(至少是2节点)
- 每个非根的分支节点都有k-1个元素 和k个孩子,其中
,每个叶子节点都有k-1个元素,其中
- 叶子节点都在同一层
- 需要满足大小大小关系(类似二叉排序树)
B+树
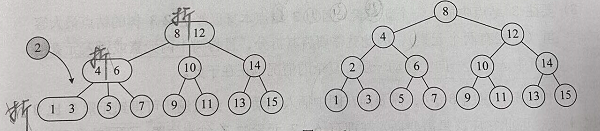
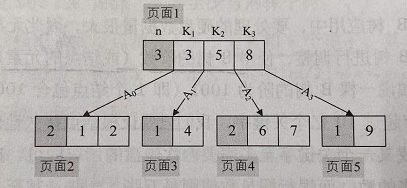
- B树有一个缺点,就是当需要遍历整颗B树,那么就要在硬盘之间多次访问,比如下图要访问 页面1 -> 页面2 -> 页面1 -> 页面3 -> 页面1 -> 页面4 -> 页面1 -> 页面5
- 这样的话,就需要多次访问父页面,这样需要多次在磁盘间访问
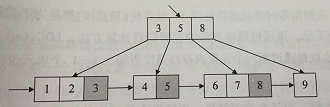
- 为了解决这个问题,在B+树中,出现在分支节点中的元素会在其中序遍历的前序叶子节点中出现。除此之外,每个叶子节点都会保存一个指向后一个叶子节点的指针。如下图:
- B+树和B树的区别:
- 叶子节点保存所有关键字信息,叶子节点按照关键字大小顺序链接
- 所有分支节点可以看成是索引,节点中仅含有其子树的最大、最小值
- 遍历B+树,从首个叶子节点开始,遍历链表即可