二站测向定位算法
1.测向原理
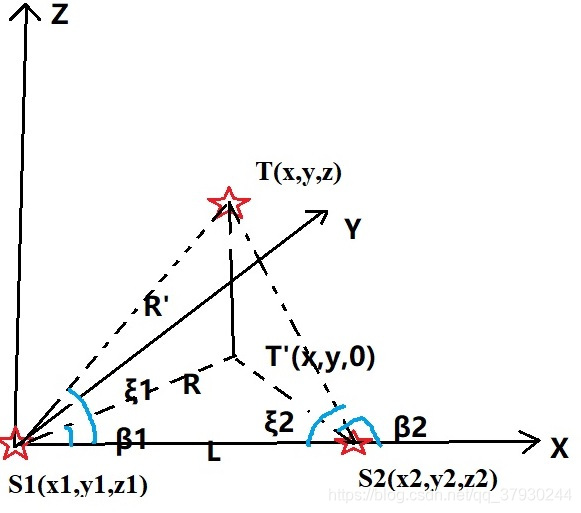
如图所示,有基站 S 1 ( x 1 , y 1 , z 1 ) , S 2 ( x 2 , y 2 , z 2 ) S_1(x_1,y_1,z_1),S_2(x_2,y_2,z_2) S1(x1,y1,z1),S2(x2,y2,z2),目标 T ( x , y , z ) T(x,y,z) T(x,y,z)。图中关键角度可由基站坐标和目标坐标表示如下:
{ tan β 1 = y − y 1 x − x 1 相 对 于 站 S 1 的 方 位 角 tan β 2 = y − y 2 x − x 2 相 对 于 站 S 2 的 方 位 角 tan ξ 1 = z − z 1 ( x − x 1 ) 2 + ( y − y 1 ) 2 相 对 于 站 S 1 的 俯 仰 角 tan ξ 2 = z − z 2 ( x − x 2 ) 2 + ( y − y 2 ) 2 相 对 于 站 S 2 的 俯 仰 角 \begin{cases} \tan\beta_1= \frac{y-y_1}{x-x_1} \quad相对于站S_1的方位角\\ \tan\beta_2= \frac{y-y_2}{x-x_2} \quad相对于站S_2的方位角\\ \tan\xi_1=\frac{z-z1}{\sqrt{(x-x_1)^2+(y-y_1)^2}} \quad相对于站S_1的俯仰角\\ \tan\xi_2=\frac{z-z2}{\sqrt{(x-x_2)^2+(y-y_2)^2}} \quad相对于站S_2的俯仰角 \end{cases} ⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧tanβ1=x−x1y−y1相对于站S1的方位角tanβ2=x−x2y−y2相对于站S2的方位角tanξ1=(x−x1)2+(y−y1)2z−z1相对于站S1的俯仰角tanξ2=(x−x2)2+(y−y2)2z−z2相对于站S2的俯仰角
由这四个角中的三个,结合基站坐标即可反推出目标位置,推导如下:
s t e p 1 : 两 基 站 间 的 距 离 L = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 + ( z 1 − z 2 ) 2 step1:两基站间的距离L=\sqrt{(x1-x2)^2+(y_1-y_2)^2+(z_1-z_2)^2} step1:两基站间的距离L=(x1−x2)2+(y1−y2)2+(z1−z2)2
s t e p 2 : 在 △ S 1 T ′ S 2 中 , 由 正 弦 定 理 得 : sin ( β 2 − β 1 ) L = sin ( π − β 2 ) R = sin ( β 2 ) R ⟹ R = L sin β 2 sin ( β 2 − β 1 ) step2:在\triangle S1 T'S2中,由正弦定理得:\frac{\sin(\beta2-\beta1)}{L}=\frac{\sin(\pi-\beta2)}{R}=\frac{\sin(\beta2)}{R}\implies R=\frac{L\sin \beta2}{\sin(\beta2-\beta1)} step2:在△S1T′S2中,由正弦定理得:Lsin(β2−β1)=Rsin(π−β2)=Rsin(β2)⟹R=sin(β2−β1)Lsinβ2
s t e p 3 : 在 △ T T ′ S 1 中 , 得 T 距 S 1 的 距 离 R ′ = R cos ξ 1 step3:在\triangle TT'S_1中,得T距S_1的距离R'=\frac{R}{\cos \xi_1} step3:在△TT′S1中,得T距S1的距离R′=cosξ1R
s t p e 4 : 可 得 : x = R ′ cos ξ 1 cos β 1 + x 1 ; y = R ′ cos ξ 1 sin β 1 + y 1 ; z = R ′ sin ξ 1 + z 1 stpe4:可得:x=R'\cos\xi_1\cos\beta_1+x_1;y=R'\cos\xi_1\sin\beta_1+y_1;z=R'\sin\xi_1+z_1 stpe4:可得:x=R′cosξ1cosβ1+x1;y=R′cosξ1sinβ1+y1;z=R′sinξ1+z1
2.误差推导
条件:
S 1 ( x 1 , y 1 , z 1 ) S 2 ( x 2 , y 2 , z 2 ) T ( x , y , z ) S_1(x_1,y_1,z_1) \qquad S_2(x_2,y_2,z_2) \qquad T(x,y,z) S1(x1