87. 扰乱字符串
思路:题目是这样的:
给定一个字符串 s1,我们可以把它递归地分割成两个非空子字符串,从而将其表示为二叉树。
下图是字符串 s1 = "great" 的一种可能的表示形式。
great
/ \
gr eat
/ \ / \
g r e at
/ \
a t
在扰乱这个字符串的过程中,我们可以挑选任何一个非叶节点,然后交换它的两个子节点。
例如,如果我们挑选非叶节点 "gr" ,交换它的两个子节点,将会产生扰乱字符串 "rgeat" 。
rgeat
/ \
rg eat
/ \ / \
r g e at
/ \
a t
我们将 "rgeat” 称作 "great" 的一个扰乱字符串。
同样地,如果我们继续交换节点 "eat" 和 "at" 的子节点,将会产生另一个新的扰乱字符串 "rgtae" 。
rgtae
/ \
rg tae
/ \ / \
r g ta e
/ \
t a
我们将 "rgtae” 称作 "great" 的一个扰乱字符串。
给出两个长度相等的字符串 s1 和 s2,判断 s2 是否是 s1 的扰乱字符串。
示例 1:
输入: s1 = "great", s2 = "rgeat"
输出: true
示例 2:
输入: s1 = "abcde", s2 = "caebd"
输出: false采用递归的方式不断将字符串从任意分割点分割,然后判断其左右部分是否满足条件即可,条件就是 交换或者未交换过,递归的终点就是要么两个字符串相等(此时判断是的已交换和不交换两种情况),相等则直接返回true,若两个字符串连元素种类和个数都不相等,则直接返回false:
public boolean isScramble(String s1, String s2) {
if (s1.equals(s2)) return true;
int n = s1.length();
int[] memo = new int[26];
for (int i = 0; i < n; ++i) {
memo[s1.charAt(i) - 'a']++;
memo[s2.charAt(i) - 'a']--;
}
for (int i = 0; i < 26; ++i) {
if (memo[i] != 0)
return false;
}
for (int i = 1; i < n; ++i) {
if ((isScramble(s1.substring(0, i), s2.substring(0, i)) && isScramble(s1.substring(i), s2.substring(i))) || (isScramble(s1.substring(0, i), s2.substring(n - i)) && isScramble(s1.substring(i), s2.substring(0, n - i)))) {
return true;
}
}
return false;
}241. 为运算表达式设计优先级
思路:由给定一个含有数字和运算符的字符串,为表达式添加括号,改变其运算优先级以求出不同的结果。你需要给出所有可能的组合的结果。有效的运算符号包含 +, - 以及 * 。
我们可以对公式中每个标点符号作为一个分割节点,将公式分成两部分分别加括号,而对这两个部分的每一个部分使用相同的方式进行递归即可。->
这样左右两边都会得到一个结果集,将其分别进行组合即可得出最终的结果集,这就是分治法。->
另外,为了进一步减少不必要的计算,比如有很多子公式(string)可能会被多次重复计算,那我们可以用一个map来记录这些公式对应的结果集,即 if(map.containsKey(input)) return map.get(input),由于我们需要不断地递归,所以map不能直接放在函数体中,要把map作为一个全局变量:
public Map<String, List<Integer>> map = new HashMap<>();对于函数体的内容:
if(map.containsKey(input)) return map.get(input);
List<Integer> list = new ArrayList<>();
int len = input.length();
for(int i = 0; i < len; i++) {
char c = input.charAt(i);
if(c == '+' || c == '-' || c == '*') { // 出现运算符号,递归求解前半段和后半段。
List<Integer> left = diffWaysToCompute(input.substring(0, i));//用left和right接住了回溯中的list,所以上面函数里的list是必要的,因为会用于接住每次调用所需要的left和right
List<Integer> right = diffWaysToCompute(input.substring(i+1, input.length())); // -1 => left:[[0]] right:[[1]]
for(int l : left) {
for(int r : right) {
switch(c) {
case '+':
list.add(l + r);
System.out.println(list);
break;
case '-':
list.add(l - r);
System.out.println(list);
break;
case '*':
list.add(l * r);
System.out.println(list);
break;
}
}
}
}
}当递归到列表只剩下一个数字的时候(因为没有运算符号所以list最终会为空,这里相当于递归的出口,是必须要考虑这种情况的),直接add进list即可:
if(list.size() == 0) list.add(Integer.valueOf(input)); // 单独一个数字的情况 (可能出现多位数)
map.put(input, list);
return list;所以分治法的思想还是递归思想。
95. 不同的二叉搜索树 II
思路:给定一个数字 n,要求生成所有值为 1…n 的二叉搜索树。首先二叉搜索树是什么?右节点值>根节点值>左节点值。->
要构建一颗二叉搜索树,首先就要选出一个根节点,而根节点的选择是可以随意的,也就是说,只要我们选定了根节点,那么小于根节点的都放在左边,大于根节点的都放在右边,相当于就是将1…n的数分成了两个部分,这就刚好呼应了分治法的思想。->
对于根节点的左边和右边我们可以使用相同的方法也将其递归的分成两部分知道没有节点可分。
public List<TreeNode> generateTrees(int n) {
if (n < 1) {
return new LinkedList<TreeNode>();
}
return generateSubtrees(1, n);
}
private List<TreeNode> generateSubtrees(int s, int e) {
List<TreeNode> res = new LinkedList<TreeNode>();
if (s > e) {
res.add(null);
return res;
}
for (int i = s; i <= e; ++i) {
List<TreeNode> leftSubtrees = generateSubtrees(s, i - 1);
List<TreeNode> rightSubtrees = generateSubtrees(i + 1, e);
for (TreeNode left : leftSubtrees) {
for (TreeNode right : rightSubtrees) {
TreeNode root = new TreeNode(i);
root.left = left;
root.right = right;
res.add(root);
}
}
}
return res;
}这里有一个很关键的部分:
if (s > e) {
res.add(null);
return res;
}为什么s>e时要res.add(null)而不直接返回null呢?这是为了让中间的两层for循环得以执行(如果直接返回res,两个for循环不可能被执行,因为rightSubtrees和leftSubtrees都是空),这样TreeNode root = new TreeNode(i);才能被执行(避免报空指针异常)。最开始我还在generateSubtrees函数体中加了:
if(s == e){
res.add(new TreeNode(s));
return res;
} 后来发现纯属多此一举,因为for循环中就已经包含了这种情况了。
归并排序
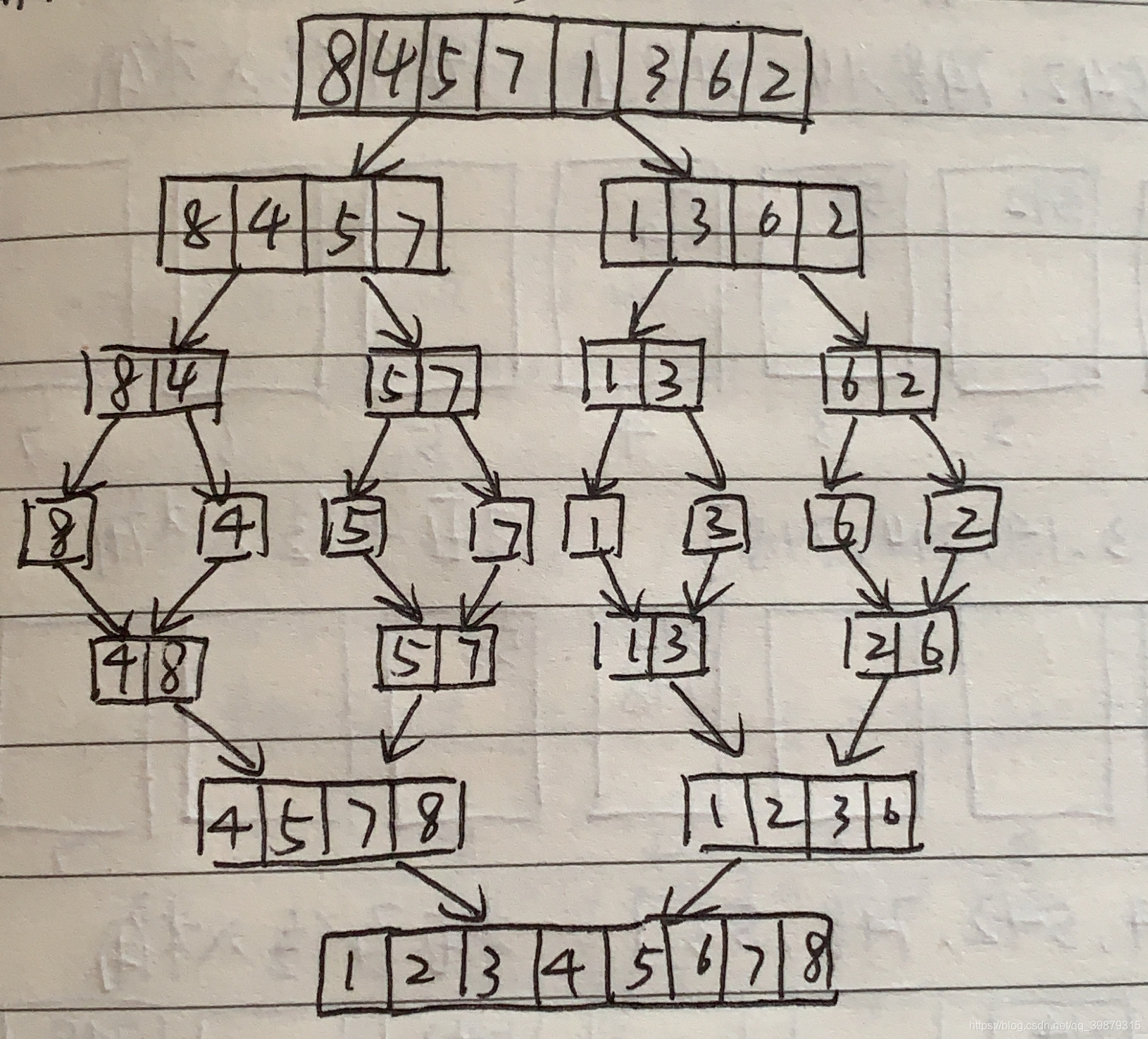
思路:归并排序就是一种很典型的分治法排序(分治法+递归),举一个简单的例子:
可以看到,基本的思路就是将数组不断地拆分成两份知道拆成一个个的数值最后再两两合并,合并过程就涉及到排序,所以刚好可以用到双指针,不断的比较两个指针所指向的数值的大小,把较小的插入到新数组中,插入后移动指针再次比较,这样就完成了数组的合并。最终合并后的数组就是排序好的数组了,代码比较简单:
public void mergeSort(int[] arr,int bgn,int end){
if(bgn>=end) return;
int mid = (bgn + end) >> 1;
mergeSort(arr,bgn,mid);
mergeSort(arr,mid+1,end);
mergeSortInOrder(arr,bgn,mid,end);//左右归并
}
public void mergeSortInOrder(int[] arr,int bgn,int mid,int end){
int l = bgn;
int m = mid + 1;
int e = end;
int[] arrs = new int[end - bgn + 1];
int k = 0;
while(l <= mid && m <= e){// 把较小的数先移到新数组中
if(arr[l] < arr[m]){
arrs[k++] = arr[l++];
}else{
arrs[k++] = arr[m++];
}
}
while(l <= mid){// 把左边剩余的数移入数组
arrs[k++] = arr[l++];
}
while(m <= e){// 把右边剩余的数移入数组
arrs[k++] = arr[m++];
}
for(int i=0;i<arrs.length;i++){// 把新数组中的数覆盖arr数组
arr[i+bgn] = arrs[i];
}
}23. 合并K个升序链表
思路:给你一个链表数组,每个链表都已经按升序排列。请你将所有链表合并到一个升序链表中,返回合并后的链表。
输入:lists = [[1,4,5],[1,3,4],[2,6]]
输出:[1,1,2,3,4,4,5,6]
解释:链表数组如下:
[
1->4->5,
1->3->4,
2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6最先能想到的就是两两合并所有的链表,如何降低合并次数呢,这就可以使用归并啦o( ̄▽ ̄)o
合并的方法比较简单,以前写过,但这里我们使用递归的版本:
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
if (l1 == null) return l2;
if (l2 == null) return l1;
ListNode head = null;
if (l1.val <= l2.val){
head = l1;
head.next = mergeTwoLists(l1.next, l2);
} else {
head = l2;
head.next = mergeTwoLists(l1, l2.next);
}
return head;
}主体方法也是采用递归,先定义递归出口:
if(lists.length == 0)
return null;
if(lists.length == 1)
return lists[0];
if(lists.length == 2){
return mergeTwoLists(lists[0],lists[1]);
}最后一个判断是必须的,只有这里才会调用合并两个链表的方法,也只有两个链表时才可以合并,其他情况继续分割:
int mid = lists.length/2;
ListNode[] l1 = new ListNode[mid];
for(int i = 0; i < mid; i++){
l1[i] = lists[i];
}
ListNode[] l2 = new ListNode[lists.length-mid];
for(int i = mid,j=0; i < lists.length; i++,j++){
l2[j] = lists[i];
}最后再递归:
return mergeTwoLists(mergeKLists(l1),mergeKLists(l2));完整代码如下:
public ListNode mergeKLists(ListNode[] lists){
if(lists.length == 0)
return null;
if(lists.length == 1)
return lists[0];
if(lists.length == 2){
return mergeTwoLists(lists[0],lists[1]);
}
int mid = lists.length/2;
ListNode[] l1 = new ListNode[mid];
for(int i = 0; i < mid; i++){
l1[i] = lists[i];
}
ListNode[] l2 = new ListNode[lists.length-mid];
for(int i = mid,j=0; i < lists.length; i++,j++){
l2[j] = lists[i];
}
return mergeTwoLists(mergeKLists(l1),mergeKLists(l2));
}
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
if (l1 == null) return l2;
if (l2 == null) return l1;
ListNode head = null;
if (l1.val <= l2.val){
head = l1;
head.next = mergeTwoLists(l1.next, l2);
} else {
head = l2;
head.next = mergeTwoLists(l1, l2.next);
}
return head;
}