算法模板总结
- 滑动窗口
- 双指针算法
- 链表操作
- 几数之和
- KMP(字符串)
- 栈
- 队列
- 二叉树
- Map
- Set
- 动态数组`List<> list`
- 可变字符串
- 只使用常量额外空间 ==>位运算
- 时间复杂度
- 前缀树
- 回溯算法
- 贪心算法
- 动态规划
- 图论
- 单调栈
- 前缀数组
- 差分数组
- 单例模式
- 简单工厂
- 写三个线程交替打印ABC
- 排序相关
- Top K问题
- 设计LRU缓存
- 三个线程交替打印ABC
- 求最大公约数 `gcd(a,b)`
- ACM模式中建树建表和建图
- 工具:IntStream、LongStream 和 DoubleStream
- 创建IntStream流(IntStream中的静态方法:of / builder/ range / rangeClosed / generate / iterate)
- `filter()` 方法过滤出符合条件的数据
- `map()`方法对流中所有元素执行某个修改操作
- `mapToObj` / `mapToLong` / `mapToDouble` / `asLongStream` / `asDoubleStream`
- `forEach` / `forEachOrdered`
- `distinct()`方法
- `sorted()` 方法
- `skip`
- `sum / min / max / count / average / summaryStatistics`
- `boxed()`
- `toArray()`
- 例子
滑动窗口
(摘自labuladong算法小抄)
滑动窗口一般用来解决寻找子串问题
int left = 0, right = 0;
while (right < s.size()) {
// 增大窗口
window.add(s[right]);
right++;
while (window needs shrink) {
// 缩小窗口
window.remove(s[left]);
left++;
}
}
双指针算法
数组相关
合并两个有序数组
设置两个指针p1,p2分别指向数组头部,再设置一个指针p3指向新数组头部
分别比较p1 p2的大小,小的指针前移且赋值于p3
左右指针技巧
就是两个指针相向而行或者相背而行
- 两数相加和=target (有序数组)
- 左右指针分列两端,和>target ⇒ right–,反之left++,和=target ⇒ 记录并左右同时收缩,直到left !< right
快慢指针技巧
使用一快一慢同向指针,
- 在有序数组中去重
- 我们让慢指针 slow 走在后面,快指针 fast 走在前面探路,找到一个不重复的元素就赋值给 slow 并让 slow 前进一步。这样,就保证了 nums[0…slow] 都是无重复的元素,当 fast 指针遍历完整个数组 nums 后,nums[0…slow] 就是整个数组去重之后的结果
- 原地删除/修改数组
- 如果 fast 遇到值为 val 的元素,则直接跳过,否则就赋值给 slow 指针,并让 slow 前进一步。
字符串相关
左右指针
反转字符串问题
左右指针从两端向中间移动,保持left<right
快慢指针
替换空格字符问题
慢指针slow=0,快指针遍历字符串
当str[fast]!=' '时,快慢指针同时前移赋值,注意慢指针要在每个单词前加上空格(除了第一个)
private char[] deleteSpace(char[] str){
int slow = 0;
for(int fast = 0; fast<str.length; fast++){
if(str[fast] != ' '){ //只处理非空格
if(slow > 0){
str[slow++] = ' ';//额外加上单词间的空格
}
while(fast < str.length && str[fast] != ' '){
str[slow++] = str[fast++];
}
}
}
char[] newStr = new char[slow];
for(int i = 0; i< slow; i++){
newStr[i] = str[i];
}
return newStr;
}
链表相关
快慢双指针
删除链表的倒数第N个节点
快指针先前进n步,之后快慢指针同时前进,当快指针指向最后一个节点时,慢指针的下一个节点就是要删除的点
链表相交
快指针在长链表上前进(长链表长度-短链表长度)步,慢指针指向短链表头部,之后只要快!=慢,就同时前进
环形链表
快慢指针,快指针一次两步,慢指针一次一步,如果fast==slow,说明有环,此时一个指针放在head,一个指针在相交处,每次向前同时移一步,相交处即为入环的第一个节点
链表操作
链表操作一般都要设置一个虚拟头节点,这样不用特殊处理原头节点
特别是操作后还需要返回新的头节点时
143. 重排链表
题目说在原链表上操作,所以不能用栈啊或者双向队列重新拷贝之类的方法
1.快慢指针找到中点 2.拆成两个链表 3.遍历两个链表,后面的塞到前面的“缝隙里”
public void reorderList(ListNode head) {
ListNode fast = head, slow = head;
while(fast.next != null && fast.next.next != null){
slow = slow.next;
fast = fast.next.next;
}
ListNode lastHead = slow.next;
slow.next = null;
// 反转后面链表
ListNode reversedLastHead = reverse(lastHead);
// 回填
while(head != null && reversedLastHead != null){
ListNode temp = head.next;
ListNode lastTemp = reversedLastHead.next;
head.next = reversedLastHead;
reversedLastHead.next = temp;
head = temp;
reversedLastHead = lastTemp;
}
}
private ListNode reverse(ListNode head){
ListNode pre = null;
ListNode cur = head;
while(cur != null){
ListNode temp = cur.next;
cur.next = pre;
pre = cur;
cur = temp;
}
return pre;
}
328. 奇偶链表
public ListNode oddEvenList(ListNode head) {
if(head == null) return head;
ListNode oddHead = head, evenHead = head.next;
ListNode o = oddHead, e = evenHead;
while(o != null && e != null && e.next != null){
ListNode temp1 = o.next.next;
ListNode temp2 = e.next.next;
o.next = temp1;
e.next = temp2;
o = temp1;
e = temp2;
}
o.next = evenHead;
return head;
}
几数之和
两数之和
使用HashMap(存储数字和对应的idx)
依次遍历数组,如果存在key==(target-num),则返回当前num的idx和找到的key的idx
四个数组的四数之和
使用HashMap(存储数字和与对应和出现的次数)
先遍历前两个数组,存储每一个和与出现的次数
之后遍历后两个数组,找map里是否有target-(num3+num4) ,有的话+对应的次数
for(int num1 : nums1){
for(int num2: nums2){
int temp = num1+num2;
map.put(temp, map.getOrDefault(temp, 0) + 1);
}
}
for(int num3 : nums3){
for(int num4 : nums4){
int temp = num3+num4;
if(map.containsKey(0-temp)){
res += map.get(0-temp);
}
}
}
三数之和
答案中不能包涵重复的三元组
不需要返回原来排序前的idx
现将数组排序,然后外层for循环i从0开始,同时定义左右指针left=i+1,right=末尾,之后保持left<right状态左右逼近
此时还需要去重:
public List<List<Integer>> threeSum(int[] nums) {
Arrays.sort(nums);
List<List<Integer>> res = new ArrayList<>();
for(int i = 0; i<nums.length-2; i++){
int left = i+1, right = nums.length-1;
if(nums[i] > 0) break; //剪枝
if(i>0 && nums[i] == nums[i-1]) continue; //去重a
while(left < right){
int temp = nums[i] + nums[left] + nums[right];
if(temp == 0){
List<Integer> path = new ArrayList<>();
path.add(nums[i]);
path.add(nums[left]);
path.add(nums[right]);
res.add(path);
// 去重bc,同时不会出现 当遇到[0,0,0,0]时,不记录一组解 的情况
while(left<right && nums[right-1] == nums[right]) right--;
while(left<right && nums[left+1] == nums[left]) left++;
left++;
right--; //同时收缩
}else if(temp < 0){
left++;
}else{
right--;
}
}
}
return res;
}
同一数组中四数之和
答案中不能包涵重复的三元组
不需要返回原来排序前的idx
和三数差不多 a+b+c+d=target
这里还要多去重一个b
for(int i = 0; i < nums.length-3; i++){
for(int j = i+1; j< nums.length-2; j++){
if(nums[i] >target && nums[i] >0) break;
if(i > 0 && nums[i] == nums[i-1]) continue; //去重a
if(j > i+1 && nums[j] == nums[j-1]) continue; //去重b
int left = j+1, right = nums.length-1;
while(left < right){
int temp = nums[i] + nums[j] + nums[left] + nums[right];
if(temp < target){
left++;
}else if(temp > target){
right--;
}else{
List<Integer> path = new ArrayList<>();
path.add(nums[i]);
path.add(nums[j]);
path.add(nums[left]);
path.add(nums[right]);
res.add(path);
while(left<right && nums[right-1] == nums[right]) right--;
while(left<right && nums[left+1] == nums[left]) left++; //去重cd
left++;
right--;
}
}
}
}
如果target !=0,这里不能再剪枝nums[i]>target,因为还有可能越加越小
可以if(nums[i] >target && nums[i] >0) break;
KMP(字符串)
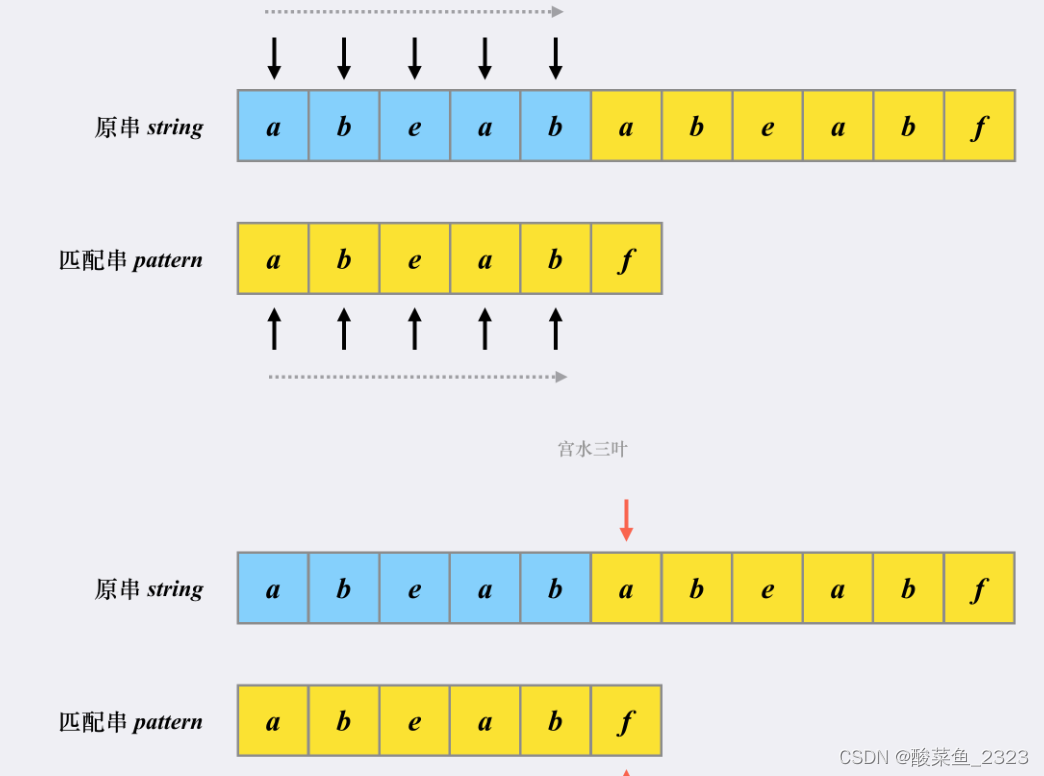
KMP算法是一个快速查找匹配串的算法,作用:如何快速在「原字符串」中找到「匹配字符串」。(leetcode28题)
如果逐一循环套循环的朴素解法,时间复杂度
O
(
m
∗
n
)
O(m*n)
O(m∗n),而KMP算法的复杂度为
O
(
m
+
n
)
O(m+n)
O(m+n)。
KMP 能在「非完全匹配」的过程中提取到有效信息进行复用,以减少「重复匹配」的消耗。不用每一次都从头再次循环查找
举例:
- 此时’a’ 和‘f’匹配不上,朴素解法会从原串的匹配起始位置+1的’b‘开始重新和匹配串匹配。
- 而KMP不会重新匹配
先了解什么是next数组
前缀表
next数组其实是一个前缀表,用来回退的,它记录了模式串与主串(文本串)不匹配的时候,模式串应该从哪里开始重新匹配。
什么是前缀表?记录下标i之前(包括i)的字符串中,有多大长度的相同前缀后缀。
刚才的例子中,KMP会利用前缀表从‘e’开始继续匹配。(匹配串中相同前缀的后面)
如何计算前缀表

在计算出前缀表后,如何利用前缀表跳转?
模式串与前缀表对应位置的数字表示的就是:下标i之前(包括i)的字符串中,有多大长度的相同前缀后缀。
很多KMP算法的时间都是使用next数组来做回退操作,那么next数组与前缀表有什么关系呢?
next数组就可以是前缀表,但是很多实现都是把前缀表统一减一(右移一位,初始位置为-1)之后作为next数组。
具体实现中:next数组既可以就是前缀表,也可以是前缀表统一减一(右移一位,初始位置为-1)。
使用next数组匹配
以下我们以前缀表统一减一之后的next数组来做演示。
有了next数组,就可以根据next数组来 匹配文本串s,和模式串t了。
class Solution {
public:
void getNext(int* next, const string& s) {
int j = -1;
next[0] = j;
for(int i = 1; i < s.size(); i++) { // 注意i从1开始
while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
j = next[j]; // 向前回退
}
if (s[i] == s[j + 1]) { // 找到相同的前后缀
j++;
}
next[i] = j; // 将j(前缀的长度)赋给next[i]
}
}
int strStr(string haystack, string needle) {
if (needle.size() == 0) {
return 0;
}
int next[needle.size()];
getNext(next, needle);
int j = -1; // // 因为next数组里记录的起始位置为-1
for (int i = 0; i < haystack.size(); i++) { // 注意i就从0开始
while(j >= 0 && haystack[i] != needle[j + 1]) { // 不匹配
j = next[j]; // j 寻找之前匹配的位置
}
if (haystack[i] == needle[j + 1]) { // 匹配,j和i同时向后移动
j++; // i的增加在for循环里
}
if (j == (needle.size() - 1) ) { // 文本串s里出现了模式串t
return (i - needle.size() + 1);
}
}
return -1;
}
};
参考题解:
链接:https://leetcode.cn/problems/find-the-index-of-the-first-occurrence-in-a-string/solutions/575568/shua-chuan-lc-shuang-bai-po-su-jie-fa-km-tb86/
栈
定义
Stack<T> st = new Stack<>();
st.push();
st.pop();
st.peek();
st.isEmpty();
常见问题
括号匹配
设置一个栈存放左括号,遇到右括号时弹出匹配(此时如果栈为空也是false),最后栈中无元素为true
删除字符串中所有相邻重复项
设置栈存放字符,如果和现有栈顶元素重复,则弹出
逆波兰表达式
把所有数字存在栈中,遇到符号,就弹出两个数做运算,再把结果压回栈内
队列
队列中是对象,不能直接d.peek() == q.peek(),要是用equals() 来比较
普通队列定义
Queue<T> que = new LinkedList<>();
que.offer();
que.poll();
que.peek();
que.size();
双端队列
Deque<T> que = new LinkedList<>();
que.add(val);
// 队头出队
que.poll();
// 队尾出队
que.removeLast();
// 获取队头元素
que.peek()
// 获取队尾元素
que.getLast();
优先级队列(大小顶堆)
Queue<T> que = new PriorityQueue<>((x,y)->(y-x)); //大顶堆
Queue<T> que = new PriorityQueue<>(); //小顶堆
当T为Long时的优先级队列
Queue<Long> pri_que = new PriorityQueue<>((x,y)->{
if(y-x > 0) return 1;
if(y.equals(x)) return 0;
return -1;
});
经典问题
前k个高频元素
优先级队列的排序规则可以自定义,如下,存储数组根据数组第二个元素排序:
Queue<int[]> que = new PriorityQueue<>((pair1,pair2)->(pair2[1]-pair1[1]));//定义大根堆,根据次数排序
for(Map.Entry<Integer,Integer> entry : map.entrySet()){
que.offer(new int[]{entry.getKey(), entry.getValue()}); //存储[num, cnt]数组
}
单调队列
经典问题
求滑动窗口最大值
如何求窗口内的最大值,如果窗口过大,每次求最大值会超时。
如果使用大顶堆(优先级队列),窗口是移动的,而大顶堆每次只能弹出最大值,我们无法移除其他数值,大顶堆不能动态维护滑动窗口里面的数值。所以不能用大顶堆
因此,需要一个单调队列,随着窗口的移动,队列也一进一出,每次移动之后,队列告诉我们里面的最大值是什么。
怎么每次移除窗口最左端元素,而不是最大最小值呢?
其实队列没有必要维护窗口里的所有元素,只需要维护有可能成为窗口里最大值的元素就可以了,同时保证队列里的元素数值是由大到小的。

设计单调队列的时候,pop,和push操作要保持如下规则:
- pop(value):如果窗口移除的元素value等于单调队列的出口元素,那么队列弹出元素,否则不用任何操作
- push(value):如果push的元素value大于入口元素的数值,那么就将队列入口的元素弹出,直到push元素的数值小于等于队列入口元素的数值为止
保持如上规则,每次窗口移动的时候,只要问que.front()就可以返回当前窗口的最大值。

自定义数据结构实现单调队列:
class MyQueue {
Deque<Integer> deque = new LinkedList<>();
//弹出元素时,比较当前要弹出的数值是否等于队列出口的数值,如果相等则弹出
//同时判断队列当前是否为空
void poll(int val) {
if (!deque.isEmpty() && val == deque.peek()) {
deque.poll();
}
}
//添加元素时,如果要添加的元素大于入口处的元素,就将入口元素弹出
//保证队列元素单调递减
//比如此时队列元素3,1,2将要入队,比1大,所以1弹出,此时队列:3,2
void add(int val) {
while (!deque.isEmpty() && val > deque.getLast()) {
deque.removeLast();
}
deque.add(val);
}
//队列队顶元素始终为最大值
int peek() {
return deque.peek();
}
}
二叉树
一般遍历整个树的没有返回值,遍历单条路径的有返回值
二叉树的前序中序后序遍历
递归法
前序:
List<Integer> res = new ArrayList<>();
public List<Integer> preorderTraversal(TreeNode root) {
//递归方法
preOrder(root);
return res;
}
private void preOrder(TreeNode root){
if(root == null) return;
res.add(root.val); //根
preOrder(root.left); //左
preOrder(root.right); //右
}
非递归法(迭代法)
用栈存储类似递归的结果
前序:(后序类似)
List<Integer> res = new ArrayList<>();
public List<Integer> preorderTraversal(TreeNode root) {
//迭代法
if(root == null) return res;
Stack<TreeNode> st = new Stack<>();
st.push(root);
while(!st.isEmpty()){
TreeNode temp = st.pop();
res.add(temp.val);
if(temp.right != null){ //右
st.push(temp.right);
}
if(temp.left != null){ //左
st.push(temp.left);
}
}
return res;
}
中序:
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
//非递归法
Stack<TreeNode> st = new Stack<>();
if(root == null) return res;
TreeNode cur = root;
while(cur != null || !st.isEmpty()){
if(cur != null){
st.push(cur);
cur = cur.left;
}else{
if(!st.isEmpty()){
cur = st.pop();
res.add(cur.val);
cur = cur.right;
}
}
}
return res;
}
层序遍历,输出List<List<T>> 类型结果
使用`que.size()``来循环每层
List<List<Integer>> res = new ArrayList<List<Integer>>();
if(root == null) return res;
Queue<TreeNode> q = new LinkedList<>();
q.add(root);
while(!q.isEmpty()){
List<Integer> itemRes = new ArrayList<>();
int len = q.size();
while(len-- > 0){
TreeNode cur = q.poll();
itemRes.add(cur.val);
if(cur.left != null) q.add(cur.left);
if(cur.right != null) q.add(cur.right);
}
res.add(itemRes);
}
return res;
求二叉树的属性
一般是中序,通过递归函数的返回值计算
求是否对称
后序,递归的检查每个节点的左右孩子节点是否相同
求最大深度
后序,求左子树右子树的最大深度,root的深度=max(left, right)+1
private int getMaxDep(TreeNode root){
if(root == null) return 0;
int depL = getMaxDep(root.left);
int depR = getMaxDep(root.right);
return Math.max(depL, depR)+1;
}
求最小深度
后序,但此时不能求左右孩子的Math.min()+1,因为只有左孩子或者只有右孩子时强制为单边+1,只有左右孩子齐全时才和最大深度一样。
private int getMinDep(TreeNode root){
if(root == null) return 0;
int leftL = getMinDep(root.left);
int rightL = getMinDep(root.right);
if(root.left == null) return rightL + 1;
if(root.right == null) return leftL + 1;
return Math.min(leftL, rightL) + 1;
}
求有多少个节点
后序,先求左右子树的节点数,root = left+right+1
判断二叉树是否平衡
后序,递归判断每个节点的左右孩子的最大高度差是否为1
求从根节点到叶子节点的所有路径
前序,方便让父节点指向子节点,涉及回溯处理根节点到叶子的所有路径
定义List<Integer> path;,边界条件当root为叶子结点时,把path加入res集合return
之后根:path.add(root.val)
递归处理左右,递归后需要加 path.remove(path.size()-1) 做回溯
左叶子之和
后序,必须三层约束条件来判断是否是左叶子
if(root.left == null && root.right == null && flag == true){
return root.val;
}
int leftSum = sumLeaves(root.left, true);
int rightSum = sumLeaves(root.right, false);
return leftSum + rightSum;
求左下角的值(最后一行最左边)
还要再加一层深度的判断,此时当只有右孩子时不一定最左边的值是左叶子
private void leftValue(TreeNode root, boolean flag, int curDep){
if(root == null) return;
if(root.left == null && root.right == null && flag == true){
if(curDep > maxDep){
res = root.val;
maxDep = curDep;
}
}
if(root.left == null){
leftValue(root.right, true, curDep+1);
}else{
leftValue(root.left, true, curDep+1);
leftValue(root.right, false, curDep+1);
}
}
路径求和
是否有从根节点到叶子的路径之和等于目标和
后序,先判断
boolean leftPath = pathSum(root.left, curSum);
boolean rightPath = pathSum(root.right, curSum);
return leftPath || rightPath;
二叉树的修改与构造
一定是前序,先构造根节点
翻转二叉树
前序,交换左右孩子
构造二叉树
前序,要点都是先从数组中找到根的位置,然后递归从根前数组和根后数组建立 root.left 和 root.right
合并两个二叉树
前序,同时操作两个树的节点,注意合并的规则
求二叉搜索树BST的属性
中序,利用BST中序为升序数组的特性
判断是不是二叉搜索树
后序,递归判断每个节点的前驱节点和后继节点是不是位于当前root的两边
// 寻找根的前驱节点
private TreeNode findPre(TreeNode root){
TreeNode pre = root.left;
TreeNode cur = pre.right;
while(cur != null){
pre = cur;
cur = cur.right;
}
return pre;
}
//寻找根的后继节点
private TreeNode findLast(TreeNode root){
TreeNode pre = root.right;
TreeNode cur = pre.left;
while(cur != null){
pre = cur;
cur = cur.left;
}
return pre;
}
BST的最小绝对差
中序(BST中序遍历后为升序数组),用一个指针TreeNode pre; 指向每次root的前一个遍历的节点
递归更新差值
public void traversal(TreeNode root){
if(root == null) return;
traversal(root.left);
if(pre != null){
res = Math.min(res, root.val-pre.val);
}
pre = root;
traversal(root.right);
}
BST的众数
中序(BST中序遍历后为升序数组,重复的数字都在一起,可以记录cnt次数来判断是否是众数),用一个指针TreeNode pre; 指向每次root的前一个遍历的节点
但要注意一个特殊情况,树中每个节点都出现1次都是众数
private void inorder(TreeNode root){
if(root == null) return;
inorder(root.left);
if(pre != null){
if(pre.val == root.val){
curCnt++;
}else{
curCnt = 1;
}
}
pre = root;
if(curCnt > maxCnt){
maxCnt = curCnt;
res = new ArrayList<>();
res.add(root.val);
}else if(curCnt == maxCnt){
res.add(root.val);
}
inorder(root.right);
}
BST转为累加树
遍历顺序:后中左,用一个指针TreeNode pre; 指向每次root的前一个遍历的节点,代表要加的值
二叉树公共祖先问题
后序(自底向上),如果root的左右子树中分别能找到 TreeNode p, TreeNode q,那么root就为公共祖先。特殊情况,root==p/q,此时root直接就是公共祖先
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null || root == p || root == q) return root;
TreeNode l = lowestCommonAncestor(root.left, p, q); //递归向左子树找p q
TreeNode r = lowestCommonAncestor(root.right, p, q); //递归向右子树找p q
if(l == null && r == null){
return null;
}else if(l == null){
return r;
}else if(r == null){
return l;
}else{
return root;
}
}
BST的修改和构造
BST中插入
先利用BST规则进行左右子树的查找,当查到root==null时,进行插入新节点
if(root == null){
return new TreeNode(val);
}
if(root.val > val){
root.left = insertIntoBST(root.left, val);
}else if(root.val < val){
root.right = insertIntoBST(root.right, val);
}
BST删除单个节点
前序。如果删除的节点时叶子结点,直接删除如果是非叶子结点,同时左右子树俱在,需要把root的右子树放在root的前驱右边,把root的左子树覆盖为新的root节点
if(root.val == key){
if(root.left == null && root.right == null){
return null;
}else if(root.left != null && root.right == null){
return root.left;
}else if(root.left == null && root.right != null){
return root.right;
}else{ //把root的右子树放在root的前驱右边,把root的左子树覆盖为新的root节点
TreeNode temp = root.left; //前驱
while(temp.right != null){
temp = temp.right;
}
temp.right = root.right;
root = root.left;
return root;
}
}
BST修剪,可能删除多个,改变root
前序,需要递归的删除多个,甚至是改变当前root
public TreeNode trimBST(TreeNode root, int low, int high) {
if(root == null) return null;
if(root.val < low){
return trimBST(root.right, low, high); //把右子树重新做为根来求trinBST
}else if(root.val > high){
return trimBST(root.left, low, high); //把左子树重新当根
}else{
root.left = trimBST(root.left, low, high);
root.right = trimBST(root.right, low, high);
}
return root;
}
Map
map.getOrDefault(key,默认值)
Map.getOrDefault(key,默认值);
Map中会存储一一对应的key和value。
如果 在Map中存在key,则返回key所对应的的value。
如果 在Map中不存在key,则返回默认值。
可以使用 map.getOrDefault(key, new ArrayList<>()); 来初始化
map.put(key,value)
map.containsKey(key); //判断是否包含指定的键值
map.get(key); //获取指定键所映射的值
map.remove(key)
map.entrySet(); 遍历map
//使用增强for遍历
for (Map.Entry<String, String> s : map.entrySet()) {
//①可以直接输出 s 得到键值对
System.out.println(s);
//②也可以使用Entry类的方法 单独取出 键和值
String key=s.getKey(); //获取键
String value=s.getValue(); //获取值
System.out.println(key + "=" + value); //输出键值
}
Set
set.add()
Set 的add()方法
返回值:boolean类型
如果Set集合中不包含要添加的对象返回TRUE
否则返回FALSE
可以用来判断去重
set.contains(key)
set.clear()
动态数组List<> list
操作
List<> list = new ArrayList<>();
list.add()
list.get(i)
list.remove(idx)
arraylist.add(int index,E element)//可以指定位置
List转换为数组(一维int型数组不可以)list.toArray()
List变String[]:String[] ans = res.toArray(new String[]{});
二维list转数组:res.toArray(new int[res.size()][]);
数组转为List
将数组转化为list集合: Arrays.asList(对象型数据的数组)
当题目要求返回List<T> res 时,怎么每次向列表头部插入
把List声明为LinkedList
LinkedList<List<Integer>> res = new LinkedList<>();
此时有方法:res.addFirst() 实现每次头插入
最后仍可直接返回 res
LinkedList可以直接向index位置插入val
LinkedList<int[]> que = new LinkedList<>();
que.add(index, val)
可变字符串
如果字符串需要频繁修改/追加:StringBuilder
StringBuilder sb = new StringBuilder();
sb.append()//追加char c或者StringBuilder sb或String
sb.toString() //转换回String
sb.get(i)
sb.deleteCharAt(sb.length()-1);
Char[]转回String
return new String(char[]);
只使用常量额外空间 ==>位运算
- 交换律:a ^ b ^ c <=> a ^ c ^ b
- 任何数于0异或为任何数 0 ^ n => n
- 相同的数异或为0: n ^ n => 0
var a = [2,3,2,4,4]
2 ^ 3 ^ 2 ^ 4 ^ 4等价于 2 ^ 2 ^ 4 ^ 4 ^ 3 => 0 ^ 0 ^3 => 3
- 判断数偶: 奇数
x % 2 == 1偶数x % 2 == 0 - 两数取平均(除2): mid = (left+right)/2 等价于 mid = (left+right) >> 1
- 清除最低位的1: x = x&(x-1)
- 得到最低位的1: n = x & -x
- 清零: x&~x
- a^b 是无进制相加 a&b是进位信息
- 与运算 ,可获取二进制数字 num 的最右一位:
num & 1可以获得最右边一位 - 无符号右移
>>>,可获取 num 所有位的值:num >>>= 1;
时间复杂度
时间复杂度 O(logN) ==> 考虑使用二分法
归并排序、快速排序 ===> O(NlogN)
链表在O(nlgn)时间和常数空间内排序 ==>归并排序(最佳且稳定)
+ 找中间点=>用快慢指针
+ 左半部分排序 => 把mid.next=null,这样直接传入head
前缀树
包含三个单词 “sea”,“sells”,“she” 的 Trie
总结出 Trie 的几点性质:
- Trie 的形状和单词的插入或删除顺序无关,也就是说对于任意给定的一组单词,Trie 的形状都是唯一的。
- 查找或插入一个长度为 L 的单词,访问 next 数组的次数最多为 L+1,和 Trie 中包含多少个单词无关。
- Trie 的每个结点中都保留着一个字母表,这是很耗费空间的。如果 Trie 的高度为 n,字母表的大小为 m,最坏的情况是 Trie 中还不存在前缀相同的单词,那空间复杂度就为 O ( m n ) O(m^{n}) O(mn)
最后,关于 Trie 的应用场景,希望你能记住 8 个字:一次建树,多次查询。
class Trie {
class TireNode {
private boolean isEnd;
TireNode[] next;
public TireNode() {
isEnd = false;
next = new TireNode[26];
}
}
private TireNode root;
public Trie() {
root = new TireNode();
}
public void insert(String word) {
TireNode node = root;
for (char c : word.toCharArray()) {
if (node.next[c - 'a'] == null) {
node.next[c - 'a'] = new TireNode();
}
node = node.next[c - 'a'];
}
node.isEnd = true;
}
public boolean search(String word) {
TireNode node = root;
for (char c : word.toCharArray()) {
node = node.next[c - 'a'];
if (node == null) {
return false;
}
}
return node.isEnd;
}
public boolean startsWith(String prefix) {
TireNode node = root;
for (char c : prefix.toCharArray()) {
node = node.next[c - 'a'];
if (node == null) {
return false;
}
}
return true;
}
}
回溯算法
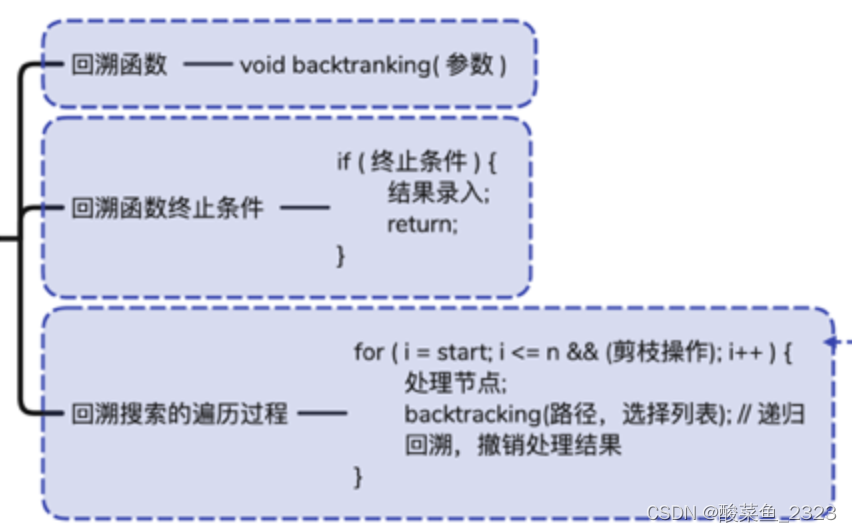
所有排列-组合-子集问题
无论是排列-组合还是子集问题,都是从序列 nums 中以给定规则取若干元素,解集不重复,有以下几种:
形式一、元素无重不可复选,即 nums 中的元素都是唯一的,每个元素最多只能被使用一次,这也是最基本的形式。
以组合为例,如果输入 nums = [2,3,6,7],和为 7 的组合应该只有 [7]。
此时不需要树层去重,如果是组合和子集需要树枝去重,排列则不需要
形式二、元素可重不可复选,即 nums 中的元素存在重复,每个元素最多只能被使用一次。
以组合为例,如果输入 nums = [2,5,2,1,2],和为 7 的组合应该有两种 [2,2,2,1] 和 [5,2]。
如果元素顺序可以改变,那么可以先把nums排序,这样相同的数字排在一起,
然后使用i>0 && nums[i] == nums[i-1] && used[i-1]==false 来树层去重。
如果是组合和子集,需要树枝去重,排列则不需要
以40题组合总和三为例:
class Solution {
List<List<Integer>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
boolean[] used; //标记数组
private int[] candidates;
private int target;
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
this.candidates = candidates;
this.target = target;
used = new boolean[candidates.length];
Arrays.sort(candidates);
backtracking(0, 0);
return res;
}
private void backtracking(int idx, int sum){
if(sum > target) return;
if(sum == target){
res.add(new ArrayList<>(path));
return;
}
for(int i = idx; i < candidates.length; i++){
if(i > 0 && candidates[i]== candidates[i-1] && used[i-1] == false) continue; //去重
path.add(candidates[i]);
sum += candidates[i];
used[i] = true;
backtracking(i+1, sum);
used[i] = false;
sum -= candidates[i];
path.remove(path.size()-1);
}
}
}
但如果nums顺序不能改变时,我们需要在每次横向遍历的操作之前,设置一个Map<Integer, Integer> map 查看当前层是否已经使用过重复的数字,不能再使用used[i-1] == false ,因为两个相同数字可能不相邻。
组合
需要树枝去重,当遍历到叶子结点时返回结果。
for(int i = idx; i < candidates.length; i++){
.....
backtracking(idx+1);//树枝去重
}
排列
不需要树枝去重,遍历到叶子结点时返回结果
for(int i = 0; i < candidates.length; i++){
.....
backtracking();
}
子集
需要树枝去重,每次递归都记录一下结果(结果集在树枝中每个节点上,而不只在叶子结点)。
private void backtracking(int idx){
res.add(new ArrayList<>(path)); //每次记录结果
if(idx == nums.length){
return;
}
for(int i = idx; i < nums.length; i++){
...
backtracking(i+1);
...
}
}
切割问题
遍历切割第几个位置idx
131.分割回文串
class Solution {
List<List<String>> res = new ArrayList<>();
List<String> path = new ArrayList<>();
String s;
public List<List<String>> partition(String s) {
this.s = s;
backtracking(0);
return res;
}
private void backtracking(int idx){
if(idx == s.length()){ //切到最后
res.add(new ArrayList<>(path));
return;
}
for(int i = idx; i<s.length(); i++){ //往后切,横向遍历每一个切割位置
String subStr = s.substring(idx, i+1);
if(isSimiliar(subStr)){
path.add(subStr);
}else{
continue;
}
backtracking(i+1);
path.remove(path.size()-1);
}
}
private boolean isSimiliar(String str){ //判断str是否是回文串
if(str.length() == 1) return true;
int left = 0, right = str.length()-1;
while(left < right){
if(str.charAt(left) != str.charAt(right)){
return false;
}
left++;
right--;
}
return true;
}
}
棋盘问题
N皇后

递归的深度是棋盘的高度(每次操作一行),for循环的宽度是棋盘的宽度
如何递归表示棋盘? 使用char[][] checkbox; 来存储棋盘
51.N皇后
输入:n = 4
输出:[[“.Q…”,“…Q”,“Q…”,“…Q.”],[“…Q.”,“Q…”,“…Q”,“.Q…”]]
class Solution {
List<List<String>> res = new ArrayList<>();
List<Integer> path = new ArrayList<>();
private int n;
char[][] checkbox;
public List<List<String>> solveNQueens(int n) {
this.n = n;
checkbox = new char[n][n];
for(char[] line : checkbox){
Arrays.fill(line, '.');
}
backtracking(0);
return res;
}
private void backtracking(int row){
if(row == n){
//存入一个答案
res.add(new ArrayList<>(chars2List(checkbox)));
return;
}
for(int col = 0; col< n; col++){
if(isValid(row, col)){
checkbox[row][col] = 'Q';
backtracking(row + 1);
checkbox[row][col] = '.';
}
}
}
private boolean isValid(int row, int col){
for(int r = 0; r< row; r++){
if(checkbox[r][col] == 'Q') return false; // 同列
}
for(int r = row-1, c = col-1; r>=0 && c>=0; r--, c--){
if(checkbox[r][c] == 'Q') return false; //左对角线
}
for(int r= row-1, c = col+1; r>=0 && c < n; r--, c++){
if(checkbox[r][c] == 'Q') return false; //右对角线
}
return true;
}
private List<String> chars2List(char[][] checkbox){
List<String> ans = new ArrayList<>();
for(char[] line : checkbox){
String temp = new String(line);
ans.add(temp);
}
return ans;
}
}
填数独
37.解数独
前面的递归都是一维递归,n皇后每行递归时只需要确定一个,
而解数独是二维递归,每一个位置都要放一个数字,并检查数字是否合法,解数独的树形结构要比N皇后更宽更深
private boolean backtracking(){
for(int row = 0; row < 9; row++){ //还需要加上行,来遍历每个位置
for(int col = 0; col < 9; col++){
if(board[row][col] == '.'){
for(int num = 1; num <= 9; num++){
if(isValid(row, col, num)){
board[row][col] = (char)(num + '0');
if(backtracking()) return true;
board[row][col] = '.';
}
}
return false;
}
}
}
return true;
安排行程
332.重新安排行程
如何存储遍历的行程机票:Map<String, Map<String, Integer>> map = new HashMap<>(); //{from : {to1:cnt1, to2:cnt2, ...}}
如何使结果的行程按字典序升序:Map<String, Integer> temp = new TreeMap<>(); // 实现按字典序排序 使用TreeMap
class Solution {
List<String> res = new ArrayList<>();
Map<String, Map<String, Integer>> map = new HashMap<>(); //{from : {to1:cnt1, to2:cnt2, ...}}
List<List<String>> tickets;
public List<String> findItinerary(List<List<String>> tickets) {
this.tickets = tickets;
for(List<String> t : tickets){
Map<String, Integer> temp;
String from = t.get(0);
if(map.containsKey(from)){
temp = map.get(from);
temp.put(t.get(1), temp.getOrDefault(t.get(1), 0)+1);
}else{
temp = new TreeMap<>(); // 实现按字典序排序
temp.put(t.get(1), 1);
}
map.put(from, temp);
}
res.add("JFK");
backtracking();
return res;
}
private boolean backtracking(){
if(res.size() == tickets.size()+1){
return true;
}
String from = res.get(res.size()-1);
if(map.containsKey(from)){
for(Map.Entry<String, Integer> tolist : map.get(from).entrySet()){
int cnt = tolist.getValue();
if(tolist.getValue() > 0){
res.add(tolist.getKey());
tolist.setValue(cnt-1);
if(backtracking()) return true;
tolist.setValue(cnt);
res.remove(res.size()-1);
}
}
}
return false;
}
}
贪心算法
贪心常识题
455. 分发饼干
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
两个数组分别排序,然后用小饼干喂小胃口
for(int i = 0; i < s.length; i++){
if(cnt < g.length && g[cnt] <= s[i]) cnt++;
}
1005. K 次取反后最大化的数组和
给你一个整数数组 nums 和一个整数 k ,按以下方法修改该数组:选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。重复这个过程恰好 k 次。可以多次选择同一个下标 i 。以这种方式修改数组后,返回数组 可能的最大和 。
把数组按绝对值大小从大到小排序,然后遍历时遇到负数取反。
如果还有多的k,那么全用在最小的数字上
nums = IntStream.of(nums).boxed()
.sorted((o1,o2) -> Math.abs(o2)-Math.abs(o1))
.mapToInt(Integer::intValue).toArray();
860. 柠檬水找零
找零钱问题:
给你一个整数数组 bills ,其中 bills[i] 是第 i 位顾客付的账。如果你能给每位顾客正确找零,返回 true ,否则返回 false 。
遇到5块钱:five++
遇到10块钱:ten++, five–;
遇到20块钱:首先用10元找零,ten–, five–;
没有10元的话,five -=3
贪心找规律题
376. 摆动序列
给你一个整数数组 nums ,返回 nums 中作为 摆动序列 的 最长子序列的长度 。
将数字按大小画出来,摆动序列应该数字在峰顶峰底交替
使用dp动态规划,dp[i][0]:第i个数在山谷的最长子序列长度, dp[i][1]:第i个数在山峰的最长子序列长度
由于摆动子序列可以不连续,所以dp数组递归赋值时,需要每次都往前从头找一次来循环赋值
for(int i = 1; i < nums.length; i++){ // 递归赋值dp
dp[i][0] = dp[i][1] = 1; //i 自己可以成为波峰或者波谷
for(int j = 0; j< i; j++){ // 子序列可以不连续,每次都要从头
if(nums[j] > nums[i]){ //遍历赋值山谷,找到之前最大的山顶+1
dp[i][0] = Math.max(dp[i][0], dp[j][1]+1);
}
if(nums[j] < nums[i]){ //遍历赋值山峰,找到之前最大的山谷+1
dp[i][1] = Math.max(dp[i][1], dp[j][0]+1);
}
}
}
return Math.max(dp[nums.length-1][0], dp[nums.length-1][1]);
738. 单调递增的数字
给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。
如果遇到nums[i-1] > nums[i],那么nums[i-1] -1, nums[i] = 9
循环从后往前递归判断,由于可能发生多次变化,在这里使用flag标记开始为9的位置,最后再循环赋值9
两个维度权衡问题
135. 分发糖果
n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。你需要按照以下要求,给这些孩子分发糖果:每个孩子至少分配到 1 个糖果。相邻两个孩子评分更高的孩子会获得更多的糖果。请你给每个孩子分发糖果,计算并返回需要准备的 最少糖果数目 。
此时,需要中间的数字比左边和右边都大。
因此需要进行两次遍历,一次确定一个维度。
从前往后遍历一边(比左大),再从后往前遍历一边(比右大),保证如果孩子比左右分数都高时,糖果数比左右都大。
for(int i = 1; i<candies.length; i++){
if(ratings[i] > ratings[i-1]) candies[i] = candies[i-1] + 1;
}
for(int i = candies.length-2; i >= 0; i--){
if(ratings[i] > ratings[i+1]) candies[i] = Math.max(candies[i], candies[i+1] + 1);
}
如果题目增加了一个条件:小朋友围成了一个环
在首尾补充两个元素,首部补充原尾部元素,尾部补充原首部元素,计算方法还是一样的,只是最后求和的时候刨去添加的首尾
406. 根据身高重建队列
假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。
先根据身高h从大到小排序,然后再根据k从高往低把people放到第k个位置,这样每次插入的都是大值,第k个位置前的都比自己大。
// 身高从大到小排(身高相同k小的站前面)
Arrays.sort(people, (a,b)->{
if(a[0] == b[0]) return a[1]-b[1];
else return b[0]-a[0];
});
LinkedList<int[]> que = new LinkedList<>();
for(int[] p : people){
que.add(p[1], p);
}
return que.toArray(new int[que.size()][2]);
区间贪心
452. 用最少数量的箭引爆气球
用最少的弓箭射爆所有气球,其本质就是找到不重叠区间数。
现将区间按左节点从小到大排序

int cnt = 1;
int startY = points[0][1];
for(int i = 1; i<points.length; i++){
if(points[i][0] > startY){
cnt++;
startY = points[i][1];
}else{
startY = Math.min(points[i][1], startY);
}
}
435. 无重叠区间
给定一个区间的集合 intervals ,其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量,使剩余区间互不重叠 。
计算重叠区间,每次保存重叠区间的最小右节点,来保证移除的最少
int cnt = 0;
int startY = intervals[0][1];
for(int i = 1; i<intervals.length; i++){
if(intervals[i][0] < startY){
cnt++;
startY = Math.min(startY, intervals[i][1]);
}else{
startY = intervals[i][1];
}
}
55. 跳跃游戏二
每次保存当前能到达的最大距离,如果到了尽头还没到终点,那么跳跃次数增加,更新最大距离
int curLoc = 0; // 当前跳转步数能走的最大距离
int farLoc = 0; // 不断更新到尽头前下次跳转的最大距离
int cnt = 0;
for(int i = 0; i < nums.length-1; i++){ //注意这里是<num.length-1,如果在倒数第二个位置还没有到达curLoc,那么肯定能到达末尾且无需跳转
// if(farLoc < i + nums[i]){
// farLoc = i + nums[i];
// cnt++;
// }
farLoc = Math.max(farLoc, i + nums[i]);
if(i == curLoc){ //到达当前能走的最大范围
curLoc = farLoc;//此时更新走过的数组中能跳转的最远距离
cnt++;
}
}
加油站
此问题不能使用两层循环,会超时
可以换思路:
首先如果总油量减去总消耗大于等于零那么一定可以跑完一圈,说明 各个站点的加油站 剩油量rest[i]相加一定是大于等于零的。
每个加油站的剩余量rest[i]为gas[i] - cost[i]。
i从0开始累加rest[i],和记为curSum,一旦curSum小于零,说明[0, i]区间都不能作为起始位置,因为这个区间选择任何一个位置作为起点,到i这里都会断油,那么起始位置从i+1算起,再从0计算curSum
那么局部最优:当前累加rest[i]的和curSum一旦小于0,起始位置至少要是i+1,因为从i之前开始一定不行。全局最优:找到可以跑一圈的起始位置
int total_rest = 0;
int cur_rest = 0;
int start = 0;
for(int i = 0; i<gas.length; i++){
total_rest += (gas[i]-cost[i]);
cur_rest += (gas[i]-cost[i]);
if(cur_rest < 0){
start = i+1;
cur_rest = 0;
}
}
return total_rest < 0 ? -1: start;
监控二叉树状态
每个节点有三种状态:0:未被监控;1:已被监控;2:此节点有照相机
递归自底向上来根据节点状态,判断是否需要加照相机
class Solution {
int res = 0;
public int minCameraCover(TreeNode root) {
if(backtracking(root) == 0) res++;
return res;
}
private int backtracking(TreeNode root){
if(root.left == null && root.right == null) return 0; //root没有被监视
int leftV = 0, rightV = 0;
if(root.left != null && root.right != null){
leftV = backtracking(root.left);
rightV = backtracking(root.right);
}else if(root.left == null){
rightV = backtracking(root.right);
leftV = rightV;
}else if(root.right == null){
leftV = backtracking(root.left);
rightV = leftV;
}
if(leftV == 0 && rightV == 0){
res++;
return 2; //root放摄像头
}else if(leftV == 0 || rightV == 0){
res++;
return 2; //root放摄像头
}else if(leftV == 2 || rightV == 2){
return 1; //root被摄像头监视
}else{ //(left:1, right:1)
return 0;
}
}
}
动态规划
动规基础
dp五部曲
- 定义dp数组含义
- 递推公式
- 初始化dp数组
- 根据递推公式 确定遍历顺序
- 举例推导dp数组
746. 使用最小花费爬楼梯
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
public int minCostClimbingStairs(int[] cost) {
int[] dp = new int[cost.length+1];
dp[0] = 0; //一开始不跳不花费
dp[1] = 0;
for(int i = 2; i <= cost.length; i++){ //顶楼还有一层需要跳到cost.length层才可以
dp[i] = Math.min(dp[i-2]+cost[i-2], dp[i-1]+cost[i-1]);
}
return dp[cost.length];
}
相当于顶层还有一层目的地,需要跳到dp[cost.length]
343.整数拆分
给定一个正整数 n,将其拆分为至少两个正整数的和,并使这些整数的乘积最大化。 返回你可以获得的最大乘积。
public int integerBreak(int n) {
int[] dp = new int[n+1];
dp[2] = 1;
for(int i = 3; i<=n; i++){
for(int j = 1; j<= i/2; j++){ // 10->最多5+5
dp[i] = Math.max(dp[i], Math.max(j*(i-j), j*dp[i-j]));
}
}
return dp[n];
}
从1遍历j,然后有两种渠道得到dp[i]:
- 一个是j * (i - j) 直接相乘。 (拆成两个数)
- 一个是j * dp[i - j],相当于是拆分(i - j) (拆成多个数)
96. 不同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
dp[3],就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量
- 元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
- 元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
- 元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量
有2个元素的搜索树数量就是dp[2]。
有1个元素的搜索树数量就是dp[1]。
有0个元素的搜索树数量就是dp[0]。
所以dp[3] = dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]
其递推关系, dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]
j相当于是头结点的元素,从1遍历到i为止。
所以递推公式:dp[i] += dp[j - 1] * dp[i - j]; ,j-1 为j为头结点左子树节点数量,i-j 为以j为头结点右子树节点数量
public int numTrees(int n) {
int[] dp = new int[n+1];
dp[0] = 1;
for(int i = 1; i<=n; i++){
for(int j = 1; j<= i; j++){
dp[i] += dp[j-1] * dp[i-j];
}
}
return dp[n];
}
背包问题
01背包(物品只能用一次)
一维dp数组:
- 递推公式 :
dp[j] = max(dp[j], dp[j-weight[i]]+value[i]); - 遍历顺序:先遍历物品,后遍历背包;且背包时从后往前遍历(一个物品只能装一个,不能覆盖上一次遍历的结果)
416. 分割等和子集
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
target = sum(nums)/2,sum无法整除的直接返回false
需要判断是否存在一种方案使用nums物品,可以装满容量为target的背包,且总价值和也为target
for(int i = 0; i< nums.length; i++){ //遍历物品
for(int j = target; j>= nums[i]; j--){ //逆序遍历背包容量,因为1维dp正序的话会被每次覆盖dp[j-nums[i]]
dp[j] = Math.max(dp[j], dp[j-nums[i]] + nums[i]);
}
}
if(dp[target] == target) return true;
return false;
1049. 最后一块石头的重量2
一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
如果 x == y,那么两块石头都会被完全粉碎;
如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
假设存在两堆石头,它们各自和都相等,且为target = sum(stones)/2;,此时粉碎后正好为0
我们尽量把石头分为这样的两堆,因此计算用stones物品装满背包容量target后的最大价值
此时结果则为:(sum - dp[target])-dp[target]
完全背包(物品可以重复使用)
求组合
求有多少种不同的组合,不强调元素的顺序,填满背包有多少种方式?
dp数组递推时需要求和,且先遍历物品后遍历背包,从前往后遍历
递推公式:dp[j] += dp[j-nums[i]],为了求和初始化dp[0]=1
494. 目标和
给你一个整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 ‘+’ 或 ‘-’ ,然后串联起所有整数,可以构造一个 表达式 :
例如,nums = [2, 1] ,可以在 2 之前添加 ‘+’ ,在 1 之前添加 ‘-’ ,然后串联起来得到表达式 “+2-1” 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
left——正数和;right——负数和(无符号)
left-right=target
left+right=sum
==> left = (target+sum) / 2
填满容量为left的背包,用nums物品,有多少种不同的方式
if(left<0) return 0;
int[] dp = new int[left+1]; // 容量为left的背包,填满有多少种方式
dp[0] = 1; //初始化
for(int i = 0; i< nums.length; i++){
for(int j = left; j >= nums[i]; j--){
dp[j] += dp[j-nums[i]]; //所有求组合,装满背包有多少种方式,都用这个递推方程
}
}
return dp[left];
求排列
元素顺序不同也为不同的排列方法,因此外层遍历背包,内层遍历物品。
如果把遍历nums(物品)放在外循环,遍历target的作为内循环的话,举一个例子:计算dp[4]的时候,结果集只有 {1,3} 这样的集合,不会有{3,1}这样的集合,因为nums遍历放在外层,3只能出现在1后面!
dp[i] += dp[i - nums[j]],初始化dp[0]=1
377. 组合总和
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。顺序不同的序列被视作不同的组合。
// 求排列个数问题,要先遍历背包,再遍历物品
for(int i = 1; i<= target; i++){ //遍历背包
for(int j = 0; j < nums.length; j++){
if(i >= nums[j]) dp[i] += dp[i-nums[j]];
}
}
139. 单词拆分
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。
注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
boolean[] dp = new boolean[n+1];
dp[0] = true;
for(int i = 1; i<=n; i++){
for(int j = 0; j<i; j++){
String substr = s.substring(j,i);
if(wordDict.contains(substr) && dp[j]){
dp[i] = true;
break;
}
}
}
求最小数
求装满背包所有物品的最小个数
dp[j] = min(dp[j-coins[i]], dp[j]);
打家劫舍系列
设置dp数组为二维 [nums.length][2]
其中第二维表示偷/不偷两种状态下的最大金额
198. 打家劫舍
普通版本
public int rob(int[] nums) {
int[][] dp = new int[nums.length][2];
dp[0][0] = 0;
dp[0][1] = nums[0];
for(int i =1; i<nums.length; i++){
dp[i][0] = Math.max(dp[i-1][1], dp[i-1][0]);
dp[i][1] = dp[i-1][0] + nums[i];
}
return Math.max(dp[nums.length-1][0], dp[nums.length-1][1]);
}
213. 打家劫舍II
所有的房屋都围成一圈
需要把收尾状态分情况讨论
- 不考虑首元素
- 不考虑尾元素
两种情况分别进行打家劫舍计算结果,再取一个最大值
//把环分成两个数组,[0,n-1]和[1,n],然后返回最大值
int maxRes1 = oriRob(nums, 0, nums.length-2); //闭区间
int maxRes2 = oriRob(nums, 1, nums.length-1);
return Math.max(maxRes1, maxRes2);
337. 打家劫舍III
树形DP
需要后序遍历,利用左右子结点计算出的结果,计算root
每次传回一个长度为2的数组作为递归结果(偷/不偷)
public int rob(TreeNode root) {
int[] resDp = treeDp(root);
return Math.max(resDp[0], resDp[1]);
}
private int[] treeDp(TreeNode root){
int[] dp = new int[2];
if(root == null) return dp; //到达空节点,此时没值return [0,0]
int[] leftDp = treeDp(root.left);
int[] rightDp = treeDp(root.right); //后序
//处理根
dp[0] = Math.max(leftDp[0], leftDp[1]) + Math.max(rightDp[0], rightDp[1]); //不偷
dp[1] = leftDp[0] + rightDp[0] + root.val; //偷
return dp;
}
股票系列
121. 买卖股票的最佳时机
只能买卖一次,dp二维数组 dp[length][2],表示持有股票和不持有股票两种
如果第i天持有股票即dp[i][0], 那么可以由两个状态推出来
dp[i][0] = max(dp[i-1][0], -prices[i]); // 持有=(前一天就持有, 今天买入)
dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i]); //不持有=(前一天就不持有,今天卖出)
122. 买卖股票的最佳时机II
不限制股票买卖次数,dp二维数组 dp[length][2],表示持有股票和不持有股票两种
与只买卖一次不同的是:买入时需要考虑 dp[i-1][1] - prices[i]
dp[i][0] = max(dp[i-1][0], dp[i-1][1]-prices[i]); // 持有=(前一天就持有, 今天买入)
dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i]); //不持有=(前一天就不持有,今天卖出)
123. 买卖股票的最佳时机III
最多买卖2次,dp二维数组 dp[length][4],分为四种状态
- 第一次持有股票 (初始化-price[0])
- 第一次不持有股票
- 第二次持有股票 (初始化-price[0])
- 第二次不持有股票
dp[i][1] = max(dp[i-1][1], -prices[i]); //第一次买入
dp[i][2] = max(dp[i-1][2], dp[i-1][1]+prices[i]); //第一次卖出
dp[i][3] = max(dp[i-1][3], dp[i-1][2]-prices[i]); //第二次买入
dp[i][4] = max(dp[i-1][4], dp[i-1][3]+prices[i]); //第二次卖出
188.买卖股票的最佳时机IV
最多买卖K次
int[][] dp = new int[n][2*k];
for(int idx = 1; idx <= k; idx++){
dp[0][2*idx-1] = -prices[0]; //初始化
}
dp数组分奇数偶数状态分别买入卖出
for(int i = 1; i<n; i++){
for(int j = 1; j<= k; j++){
dp[i][2*j-2] = Math.max(dp[i-1][2*j-2], dp[i-1][2*j-1] + prices[i]);
if(j >= 2){
dp[i][2*j-1] = Math.max(dp[i-1][2*j-1], dp[i-1][2*(j-1)-2] - prices[i]);
}else{
dp[i][2*j-1] = Math.max(dp[i-1][2*j-1], -prices[i]);
}
}
}
return dp[n-1][2*k-2];
309. 含冷冻期问题
可以多次交易,此时可以分为三种状态:持有,不持有,在冷冻期
for(int i = 1; i < prices.length; i++){
dp[i][0] = Math.max(Math.max(dp[i-1][2], dp[i-1][0]), dp[i-1][1] + prices[i]); //卖出手无
dp[i][1] = Math.max(dp[i-1][1], dp[i-1][2] - prices[i]); //买入手持
dp[i][2] = dp[i-1][0]; //冷静期状态
}
714. 含手续费
卖出时完成一笔交易,需要减去手续费
for(int i = 1; i<prices.length; i++){
dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i] - fee);
dp[i][1] = Math.max(dp[i-1][1], dp[i-1][0] - prices[i]);
}
子序列问题(编辑距离)
子序列(不连续)
1035. 不相交的线
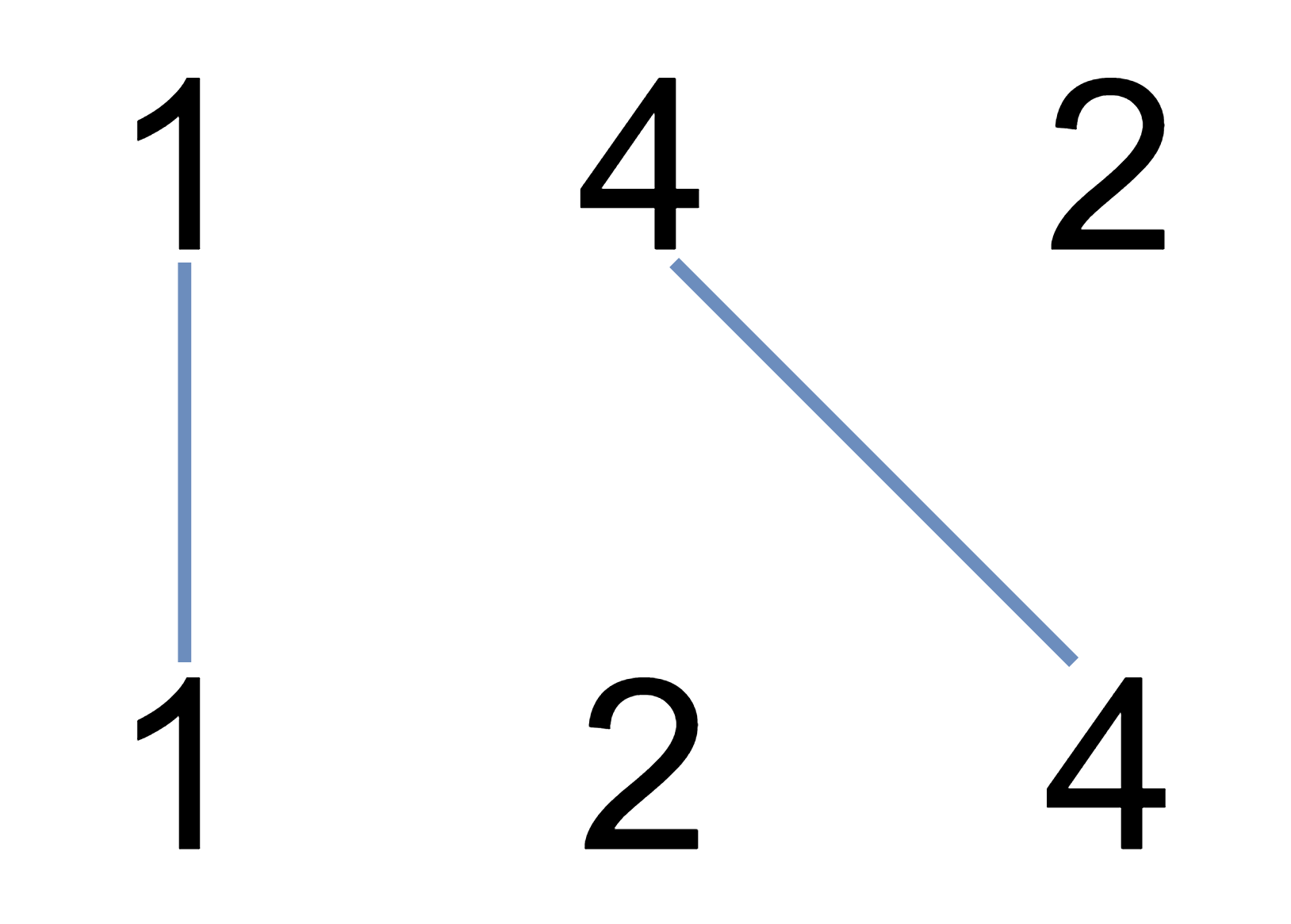
其实就是求最长公共不连续子序列长度
dp[i][j]:长度为[0,i-1]的字符串text1与长度为[0,j-1]的字符串text2的最长公共子序列长度
for(int i = 1; i<= nums1.length; i++){
for(int j = 1; j<=nums2.length;j++){
if(nums1[i-1] == nums2[j-1]){ //相等
dp[i][j] = dp[i-1][j-1] + 1;
}else{ //不相等
dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
}
}
}
子序列(连续)
连续,则只能由前一个状态推导出来
for(int i = 1; i<=nums1.length; i++){
for(int j = 1; j<=nums2.length; j++){
if(nums1[i-1] == nums2[j-1]){
dp[i][j] = dp[i-1][j-1] + 1;
}else{
dp[i][j] = 0; // 子数组不是子序列,必须连续//Math.max(dp[i-1][j], dp[i][j-1]);
}
res = Math.max(res, dp[i][j]);
}
}
编辑距离
115. 不同的子序列
给定一个字符串 s 和一个字符串 t ,计算在 s 的子序列中 t 出现的个数。
即s字符串执行多少种不同的删除字符操作,可以变为t字符串
int[][] dp = new int[s.length()+1][t.length()+1]; //在s中删除字符匹配t
//初始化
for(int i = 0; i <= s.length(); i++){
dp[i][0] = 1; //以i-1为结尾的s可以随便删除元素,出现空字符串的个数
}
for(int i = 1; i<= s.length(); i++){
for(int j = 1; j<= t.length(); j++){
if(s.charAt(i-1) == t.charAt(j-1)){
//相等时,可以使用s[i - 1]来匹配;或者删除s[i - 1](bagg -> bag)
dp[i][j] = dp[i-1][j-1] + dp[i-1][j]; //用s[i-1]和不用
}else{
dp[i][j] = dp[i-1][j];
}
}
}
72. 编辑距离
给你两个单词 word1 和 word2,请你计算出将 word1 转换成 word2 所使用的最少操作数 。
有三种操作:1.插入一个字符;2.删除一个字符;3.替换一个字符
word2添加一个元素,相当于word1删除一个元素
因此考虑只用两种状态:删除和替换
for(int i = 1; i<= word1.length(); i++){
for(int j = 1; j<= word2.length(); j++){
if(word1.charAt(i-1) == word2.charAt(j-1)){
dp[i][j] = dp[i-1][j-1];
}else{
// 删一个字符和插入一个字符的操作数一样,可以合并考虑
// 只用考虑删和替换
int del = Math.min(Math.min(dp[i-1][j]+1, dp[i][j-1]+1), dp[i-1][j-1]+2); // 删除
dp[i][j] = Math.min(del, dp[i-1][j-1]+1); //(删除,替换)
}
}
}
回文
647. 回文子串
给定一个字符串,你的任务是计算这个字符串中有多少个回文子串。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
-
当s[i]与s[j]不相等,那没啥好说的了,dp[i][j]一定是false。
-
当s[i]与s[j]相等时,这就复杂一些了,有如下三种情况
- 情况一:下标i 与 j相同,同一个字符例如a,当然是回文子串
- 情况二:下标i 与 j相差为1,例如aa,也是回文子串
- 情况三:下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]已经相同了,我们看i到j区间是不是回文子串就看aba是不是回文就可以了,那么aba的区间就是 i+1 与 j-1区间,这个区间是不是回文就看dp[i + 1][j - 1]是否为true。
for(int i = s.length()-1; i>=0; i--){
for(int j = i; j < s.length(); j++){
if(s.charAt(i) == s.charAt(j)){
if((j-i) <= 1){
cnt++;
dp[i][j] = true;
}else if(dp[i+1][j-1]){
dp[i][j] = true;
cnt++;
}
}
}
}
图论
DFS
DFS是向一个方向搜,搜到尽头才回头
- 搜索方向,是认准一个方向搜,直到碰壁之后在换方向
- 换方向是撤销原路径,改为节点链接的下一个路径,回溯的过程
代码框架:(和回溯类似)
void dfs(参数){
if(终止条件){
存放结果
return;
}
for(选择:本节点所连接的其他节点){
处理节点;
dfs(图,选择的节点); //递归
回溯,撤销处理结果
}
}
BFS
广搜适合于解决两个点之间的最短路径问题。
从起点开始,以起始点为中心一圈一圈进行搜索,一旦遇到终点,记录之前走过的节点就是一条最短路
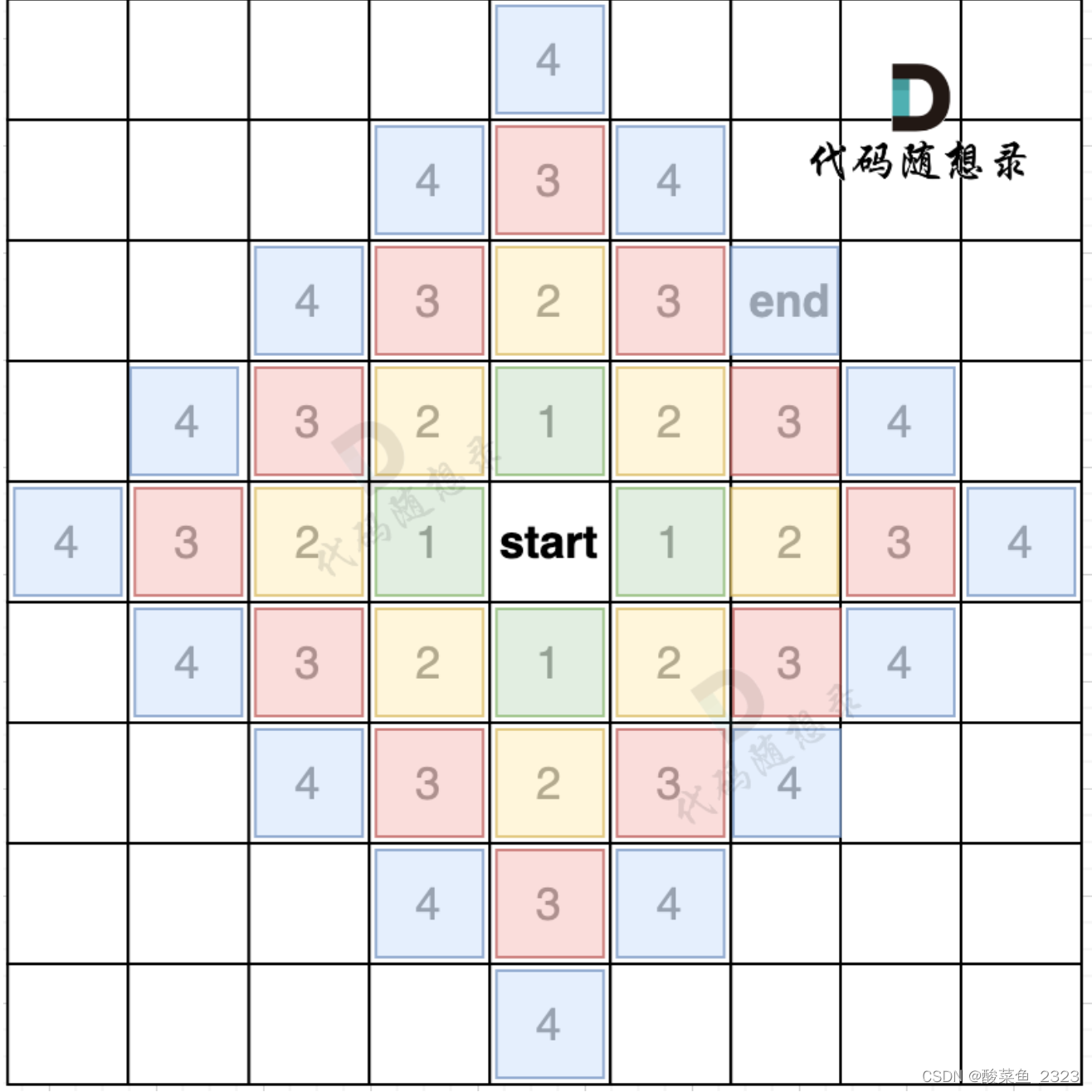
只要BFS只要搜到终点一定是一条最短路径
把一圈一圈的搜索过程放在栈/队列/数组这样的容器中。
如果放在队列,保证每一圈都是按照一个方向去转,统一顺时针或逆时针
BFS不用递归,把入口放入队列中,之后 !que.isEmpty() 进行循环,每次将队头出队,再把当前的新的选择操作后入队,
DFS与BFS举例
- 岛屿数量
DFS:
private int[] xD = {-1,1,0,0};
private int[] yD = {0,0,-1,1};
private boolean[][] visited; //标记访问过的节点,不要重复遍历,重复记录岛屿数量
private int total = 0;
private char[][] gridd; //地图
int n=0,m=0;
public int numIslands(char[][] grid) {
n = grid.length; //n×m
m = grid[0].length;
visited = new boolean[n][m];
gridd = grid;
for(int i = 0; i< n; i++){
for(int j = 0; j<m; j++){
if(visited[i][j] == false && gridd[i][j] == '1'){
dfs(i,j);
total++;
}
}
}
return total;
}
private void dfs(int x, int y){ // x,y 表示开始搜索节点的下标
visited[x][y] = true; //标记已访问过
for(int i = 0; i<4; i++){
int new_x = x + xD[i];
int new_y = y + yD[i];
if(isValid(new_x, new_y) && !visited[new_x][new_y]){
dfs(new_x, new_y); //递归访问深入
}
}
return;
}
private boolean isValid(int x, int y){
if(x < 0 || x >= n || y < 0 || y >=m) return false;
if(gridd[x][y] == '0') return false;
return true;
}
BFS:
class Solution {
private int[] xd = {-1, 1, 0, 0};
private int[] yd = {0, 0, -1, 1};
private boolean[][] visited;
private char[][] grid;
private int m,n;
public int numIslands(char[][] grid) {
int res = 0;
this.grid = grid;
m = grid.length;
n = grid[0].length;
visited = new boolean[m][n];
for(int i = 0; i< m; i++){
for(int j = 0; j<n; j++){
if(!visited[i][j] && grid[i][j] == '1'){
bfs(i,j);
res++;
}
}
}
return res;
}
// BFS
private void bfs(int x, int y){
Queue<int[]> que = new LinkedList<>();
que.offer(new int[]{x,y});
visited[x][y] = true;
while(!que.isEmpty()){ //遍历队
int[] cur = que.poll();
x = cur[0]; y = cur[1];
for(int d = 0; d<4; d++){
int nx = x + xd[d];
int ny = y + yd[d];
if(isValid(nx,ny) && !visited[nx][ny]){
que.offer(new int[]{nx, ny});
visited[nx][ny] = true; // 入队立即标记
}
}
}
}
private boolean isValid(int x, int y){
if(x < 0 || x >=m || y < 0 || y>= n) return false;
if(grid[x][y] == '0') return false;
return true;
}
}
单调栈
通常是一维数组,要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置,此时我们就要想到可以用单调栈了
单调栈的本质是空间换时间
更直白来说,就是用一个栈来记录我们遍历过的元素,存放idx数组下标
如果求一个元素右边第一个更大元素,单调栈就是从栈底到栈顶递减的,如果求一个元素右边第一个更小元素,单调栈就是从栈底到栈顶递增的
使用单调栈主要有三个判断条件。
- 当前遍历的元素T[i]小于栈顶元素T[st.top()]的情况
- 当前遍历的元素T[i]等于栈顶元素T[st.top()]的情况
- 当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况
42. 接雨水

求右边第一个更大元素 从栈底到栈顶递减
public int trap(int[] height) {
//单调栈,从栈底到栈顶递减
int res = 0;
Stack<Integer> st = new Stack<>(); //存放index
st.push(0);
for(int i = 1; i<height.length; i++){
if(height[i] < height[st.peek()]){
st.push(i);
}else if(height[i] == height[st.peek()]){
st.pop();
st.push(i);
}else{
while(!st.isEmpty() && height[i] > height[st.peek()]){
//这里要用while,如果弹出过一次后将新元素压入后还要再次判断是否要再弹出
int mid = st.pop();
if(!st.isEmpty()){
int left = st.peek();
int h = Math.min(height[left], height[i]) - height[mid];
int w = i - left -1;
res += h * w;
}
}
st.push(i);
}
}
return res;
}
84. 柱状图中最大的矩形
求右边第一个比自己小的,从栈底到栈顶递增
同时这里需要考虑第一个和最后元素栈内全部计算,因此需要在原数组前后加[0,xxx,0]
public int largestRectangleArea(int[] heights) {
//因为需要找右边第一个小于mid的,所以从低到栈顶是递增的
int res = 0;
Stack<Integer> st = new Stack<>();
//在前后加0来保证第一个和最后一个的最大矩阵也计算到
int[] newHeights = new int[heights.length + 2];
newHeights[0] = 0;
for(int i =1; i<newHeights.length-1; i++){
newHeights[i] = heights[i-1];
}
newHeights[newHeights.length-1] = 0;
st.push(0);
for(int i = 1; i<newHeights.length; i++){
if(newHeights[i] > newHeights[st.peek()]){
st.push(i);
}else if(newHeights[i] == newHeights[st.peek()]){
st.pop();
st.push(i);
}else{
while(!st.isEmpty() && newHeights[i] < newHeights[st.peek()]){
int mid = st.pop();
int w = i - st.peek() - 1;
res = Math.max(res, (newHeights[mid]*w));
}
st.push(i);
}
}
return res;
}
前缀数组
一维前缀数组:
class NumArray {
// 前缀和数组
private int[] preSum;
/* 输入一个数组,构造前缀和 */
public NumArray(int[] nums) {
// preSum[0] = 0,便于计算累加和
preSum = new int[nums.length + 1];
// 计算 nums 的累加和
for (int i = 1; i < preSum.length; i++) {
preSum[i] = preSum[i - 1] + nums[i - 1];
}
}
/* 查询闭区间 [left, right] 的累加和 */
public int sumRange(int left, int right) {
return preSum[right + 1] - preSum[left];
}
}
二维前缀数组:
class NumMatrix {
private int[][] prefix;
public NumMatrix(int[][] matrix) {
int n = matrix.length; //n行
int m = matrix[0].length; //m列
prefix = new int[n+1][m+1];
for(int i = 1; i<=n; i++){
for(int j = 1; j<=m; j++){
prefix[i][j] = prefix[i-1][j] + prefix[i][j-1] + matrix[i-1][j-1] - prefix[i-1][j-1];
}
}
}
public int sumRegion(int row1, int col1, int row2, int col2) {
return prefix[row2+1][col2+1] - prefix[row1][col2+1] - prefix[row2+1][col1] + prefix[row1][col1];
}
}
差分数组
// 差分数组工具类
class Difference {
// 差分数组
private int[] diff;
/* 输入一个初始数组,区间操作将在这个数组上进行 */
public Difference(int[] nums) {
assert nums.length > 0;
diff = new int[nums.length];
// 根据初始数组构造差分数组
diff[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
diff[i] = nums[i] - nums[i - 1];
}
}
/* 给闭区间 [i, j] 增加 val(可以是负数)*/
public void increment(int i, int j, int val) {
diff[i] += val;
if (j + 1 < diff.length) {
diff[j + 1] -= val;
}
}
/* 返回结果数组 */
public int[] result() {
int[] res = new int[diff.length];
// 根据差分数组构造结果数组
res[0] = diff[0];
for (int i = 1; i < diff.length; i++) {
res[i] = res[i - 1] + diff[i];
}
return res;
}
}
单例模式
单例模式(Singleton Pattern):保证一个类只有一个实例对象,并提供一个访问它的全局访问点。
- 把构造方法私有化
- 类本身要对外提供访问入口,全剧唯一(
static)
饿汉模式
先创建后使用 (还没有使用该单例对象就已经被加载到内存中),线程安全,占用内存。
public class EagerSingleton{
private static final EagerSingleton INSTANCE = new EagerSingleton();
private EagerSingleton(){}
public static EagerSingleton getInstance(){
return INSTANCE;
}
}
懒汉模式
用的时候才创建,线程不安全(创建或获取单例对象时),加锁会影响效率。
使用双重校验锁模式来方式线程不安全和指令重排序的问题,同时效率比synchronized声明同步方法高。
public class LazySingleton {
private static volatile LazySingleton INSTANCE = null; //防止指令重排序
private LazySingleton(){}
public static LazySingleton getInstance(){
if(INSTANCE == null){
synchronized(LazySingleton.class){
if(INSTANCE == null){ //防止前后两个线程进入等待锁,之后覆盖初始化
INSTANCE = new LazySingleton();
}
}
}
}
}
简单工厂
简单工厂模式又称为静态工厂模式:定义一个工厂类,他可以根据参数的不同返回不同类的实例,被创建的实例通常都具有相同的父类。
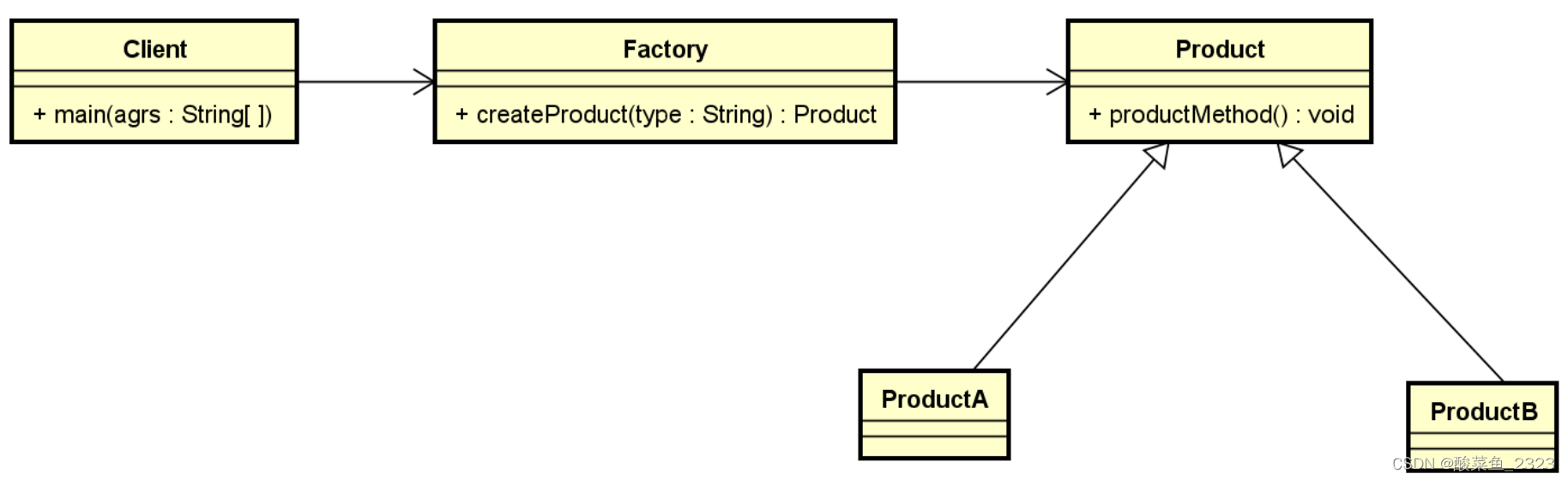
定义抽象产品类,同时定义抽象方法
/**
* 产品的抽象类
**/
public class Product{
// 描述产品的品类
public abstract void show();
}
定义具体的产品类,统一继承抽象类
/**
* 产品品系A
**/
public class ProductA extends Product{
@Override
public void show(){
System.out.println("ProductA");
}
}
/**
* 产品品系B
**/
public class ProductB extends Product{
@Override
public void show(){
System.out.println("ProductB");
}
}
定义产品具体工厂
/**
* 产品工厂 --可以选哪几种产品
**/
public class SimpleProductFactory{
/**
* 店里产品的种类
**/
public static Product createProduct(int type){
switch (type){
case 1:
return new ProductA(); //产品A
case 2:
return new ProductB(); //产品B
default:
return null;
}
}
}
*使用工厂类
public class Customer{
public static void main(String[] args){
Product p = SimpleProductFactory.createProduct(1);
p.show();
}
}
简单工厂的核心是工厂类,在没有工厂类之前,客户端一般会使用new关键字之间创建对象,而引入工厂类之后客户端可以通过工厂类来创建产品。
写三个线程交替打印ABC
排序相关
快速排序( O ( n l g n ) O(nlgn) O(nlgn))
public void quickSort(int[] nums, int low, int high){
if(low >= high) return;
int p = partition(nums, low, high);
quickSort(nums, low, p-1);
quickSort(nums, p+1, high);
}
public int partition(int[] nums, int left, int right){
int temp = nums[left];
while(left < right){
while(left < right && nums[right] > temp) right--;
nums[left] = nums[right];
while(left < right && nums[left] < temp) left++;
nums[right] = nums[left];
}
nums[left] = temp;
return left;
}
归并排序( O ( n l g n ) O(nlgn) O(nlgn))
public void mergeSort(int[] nums, int low, int high){
if(low < high){
int mid = low + (high - low) >> 2;
mergeSort(nums, low, mid);
mergeSort(nums, mid+1, high);
merge(nums, low, mid, mid+1, high);
}
}
public void merge(int[] nums, int l1, int r1, int l2, int r2){
int[] temp = new int[r2-l1+1];
int idx = 0;
int i1 = l1, i2 = l2;
while(i1 <= r1 && i2 <= r2){
if(nums[i1] <= nums[i2]){
temp[idx++] = nums[i1++];
}else{
temp[idx++] = nums[i2++];
}
}
while(i1 <= r1) temp[idx++] = nums[i1++];
while(i2 <= r2) temp[idx++] = nums[i2++];
for(int i = 0; i < idx; i++){
nums[l1+i] = temp[i];
}
}
堆排序( O ( n l g n ) O(nlgn) O(nlgn))
int[] arr = {3,4,2,1,5,8,7,6};
int n = arr.length;
public void heapSort(arr, n){
createHeap();
for(int i = n; i>=1; i--){
int temp = arr[i];
arr[i] = arr[1];
arr[1] = temp; //交换堆顶到最后一个元素
downAdjust(1, i-1); // 调整新的大顶堆(排除最后一个最大元素)
}
}
private void createHeap(){
for(int i = n/2; i>=1; i--){
downAdjust(i, n);
}
}
private void downAdjust(int i, int n){
int j = i*2;
while(j <= n){
if(j+1 <=n && arr[j+1]>arr[j]){ //找到孩子中的最大值
j = j+1;
}
if(arr[j] > arr[i]){ // 孩子节点>自己
int temp = arr[j];
arr[j] = arr[i];
arr[i] = temp;
i = j;
j = i*2;
}else{
break;
}
}
}
Top K问题
Top K 问题的常见形式:
给定10000个整数,找第K大(第K小)的数
给定10000个整数,找出最大(最小)的前K个数
给定100000个单词,求前K词频的单词
解决topK问题有许多种方法:
使用最大堆最小堆方法(求第k大的数为例)
求最大的数用小根堆,求最小的数用大根堆
(例如:求第k大的数)
顺序扫描这10000个数,然后先取出前k个数放入小根堆里。后续每扫描一个数,如果该数比堆顶小,那么直接pass;如果比堆顶大,那么把堆顶替换,之后向下调整堆一次。
最后堆内就是前topK个数,便是数组中最大的k个数,堆顶便是第k大的数。
时间复杂度为 O ( N log k)
使用Quick Select的思路(求第k大的数为例)
Quick Select脱胎于快速排序
首先选取一个枢轴pivot,然后进行一次快排,将数组中小于privot的数放在其左边,大于的放在右边
此时,如果左边的数组中的元素个数>=k,则第k大的数肯定在左边数组中,继续对左边执行相同操作;
如果个数<k,则第k大的数在右边数组,对右边执行相同操作;
如果 =k-1·,那么第k大的数就是privot
这个算法与快排最大的区别是,每次划分后只处理左半边或者右半边,而快排在划分后对左右半边都继续排序。
public int findKthLargest(int[] nums, int k) {
return quickSelect(nums, k, 0, nums.length - 1);
}
public int quickSelect(int[] nums, int k, int low, int high){
if(low == high) return nums[left];
int p = partition(nums, low, high);
if(p-low+1 < k){
quickSelect(nums,k-(p-low+1), p+1, high);
}else if(p-low+1 > k){
quickSelect(nums, k, low, p-1);
}else{
return nums[p];
}
}
设计LRU缓存
需要满足 get() 和 put()方法时间复杂度为
O
(
1
)
O(1)
O(1),那么设计的数据结构必须:
- cache中的元素必须要时间顺序,当容量满了需要删除最久未使用的元素
- 要在 cache 中快速找某个 key 是否已存在并得到对应的 val
- 每次访问cache中的某个key时,把这个元素变为最近使用的 ==> cache要支持在任意位置快速插入删除元素
哈希表查找快,但是数据无固定顺序;链表有顺序之分,插入删除快,但是查找慢。所以结合一下,形成一种新的数据结构:哈希链表 LinkedHashMap(双向链表+哈希表)。
class LRUCache {
// 选用LinkedHashMap 哈希表+双向链表
private int cap;
LinkedHashMap<Integer, Integer> map = new LinkedHashMap<>();
public LRUCache(int cap){
this.cap = cap;
}
public int get(int key){
if(!map.containsKey(key)){
return -1;
}
remoteSwitch(key);
return map.get(key);
}
public void put(int key, int value){
if(map.containsKey(key)){
map.remove(key);
map.put(key, value);
return;
}
if(map.size() + 1 > cap){
// 移除链头元素,即为最久未使用元素
int removeKey = map.keySet().iterator().next();
map.remove(removeKey);
}
map.put(key, value);
}
private void remoteSwitch(int key){
int val = map.get(key);
map.remove(key);
map.put(key, val); //把最近使用的放在链表尾部
}
}
三个线程交替打印ABC
三个线程T1、T2、T3轮流打印ABC,打印n次,如ABCABCABCABC…
synchronized + wait/notify
基本思路就是线程A、线程B、线程C三个线程同时启动,因为变量num的初始值为0,所以线程B或线程C拿到锁后,进入while()循环,然后执行wait()方法,线程线程阻塞,释放锁。只有线程A拿到锁后,不进入while()循环,执行num++,打印字符A,最后唤醒线程B和线程C。此时num值为1,只有线程B拿到锁后,不被阻塞,执行num++,打印字符B,最后唤醒线程A和线程C,后面以此类推。
参考:https://juejin.cn/post/6959078859568316452
class ThreadTest {
private int num;
private static final Object LOCK = new Object();
private void printABC(int printNum){
for(int i = 0; i< 10; i++){
synchronized(LOCK){
while(num%3 != printNum){ //轮不到当前线程就阻塞
try{
LOCK.wait();
}catch(InterruptedException e){
e.printStackTrace();
}
}
num++;
System.out.print(Thread.currentThread().getName());
LOCK.notifyAll();
}
}
}
public static void main(String[] args){
ThreadTest threadTest = new ThreadTest();
new Thread(() -> {
threadTest.printABC(0);
}, "A").start();
new Thread(() -> {
threadTest.printABC(1);
}, "B").start();
new Thread(() -> {
threadTest.printABC(2);
}, "C").start();
}
}
补充消费者生产者问题:2个线程交替打印1-100
线程odd先拿到锁——打印数字——唤醒线程even——阻塞线程odd,以此循环
class ThreadTest {
private volatile int count = 1;
private static final Object LOCK = new Object();
private void printOE(){
synchronized(LOCK){
while(count <= 100){
try{
System.out.println(Thread.currentThread().getName() + ":" + count);
count++;
LOCK.notifyAll();
LOCK.wait();
}catch(InterruptedException e){
e.printStackTrace();
}
}
}
LOCK.notifyAll();
//防止count=10后,while()循环不再执行,有子线程被阻塞未被唤醒,导致主线程不能退出
}
public static void main(String[] args){
ThreadTest threadTest = new ThreadTest();
new Thread(() -> {
threadTest.printOE();
}, "odd").start();
Thread.sleep(10);//保证线程odd先拿到锁
new Thread(()->{
threadTest.printOE();
}, "even").start();
}
}
Lock()
通过ReentrantLock我们可以很方便的进行显式的锁操作,即获取锁和释放锁,对于同一个对象锁而言,统一时刻只可能有一个线程拿到了这个锁,此时其他线程通过lock.lock()来获取对象锁时都会被阻塞,直到这个线程通过lock.unlock()操作释放这个锁后,其他线程才能拿到这个锁。
class Lock_ABC{
private int num;
private static Lock lock = new ReentrantLock();
private void printABC(int targetNum){
for(int i = 0; i<10; ){
lock.lock();
while(num % 3 == targetNum){
num++;
i++;
System.out.print(Thread.currentThread().getName());
}
lock.unlock();
}
}
public static void main(String[] args){
Lock_ABC lock_ABC = new Lock_ABC();
new Thread(() -> {
lock_ABC.printABC(0);
}, "A").start();
new Thread(() -> {
lock_ABC.printABC(1);
}, "B").start();
new Thread(() -> {
lock_ABC.printABC(2);
}, "C").start();
}
}
该方法存在问题,存在对同步锁的无意义竞争,浪费资源
可以使用Lock+Condition的方式实现对线程的精准唤醒
Lock + Condition
lock 和 await() / signal() 配合
为了能精准地唤醒下一个线程,创建了多个Condition对象
class Lock_ABC{
private int num;
private static Lock lock = new ReentrantLock();
private static Condition c1 = lock.newCondition();
private static Condition c2 = lock.newCondition();
private static Condition c3 = lock.newCondition();
private void printABC(int targetNum, Condition curThread, Condition nextThread){
for(int i = 0; i<10;){
lock.lock();
try{
while(num%3 != targetNum){
curThread.await(); // 不满足就阻塞当前线程
}
num++;
i++;
System.out.println(Thread.currentThread().getName());
nextThread.signal(); // 输出完成,唤醒下一线程
} catch (InterruptedException e){
e.printStackTrace();
}finally{
lock.unlock();
}
}
}
public static void main(String[] args){
Lock_ABC lock_ABC = new Lock_ABC();
new Thread(() -> {
lock_ABC.printABC(0, c1, c2);
}, "A").start();
new Thread(() -> {
lock_ABC.printABC(1, c2, c3);
}, "B").start();
new Thread(() -> {
lock_ABC.printABC(2, c3, c1);
}, "C").start();
}
}
Semaphore
另一种方法 用来避免唤醒其他无意义的线程避免资源浪费
Semaphore:用来控制同时访问某个特定资源的操作数量,或者同时执行某个制定操作的数量。Semaphore内部维护了一个计数器,其值为可以访问的共享资源的个数。
一个线程要访问共享资源,先使用acquire()方法获得信号量,如果信号量的计数器值大于等于1,意味着有共享资源可以访问,则使其计数器值减去1,再访问共享资源。如果计数器值为0,线程进入休眠。
当某个线程使用完共享资源后,使用release()释放信号量,并将信号量内部的计数器加1,之前进入休眠的线程将被唤醒并再次试图获得信号量。
class SemaphoreABC{
private static Semaphore s1 = new Semaphore(1); //因为先执行线程A,所以这里设s1的计数器为1
private static Semaphore s2 = new Semaphore(0);
private static Semaphore s3 = new Semaphore(0);
private void printABC(Semaphore curThread, Semaphore nextThread){
for(int i = 0; i < 10; i++){
try{
curThread.acquire(); //阻塞当前线程,即信号量的计数器减1为0
System.out.println(Thread.currentThread.getName());
nextThread.release(); //唤醒下一个线程,即信号量的计数器加1
}catch(InterruptedException e){
e.printStackTrace();
}
}
}
public static void main(String[] args){
SemaphoreABC s = new SemaphoreABC();
new Thread(() -> {
s.printABC(s1, s2);
}).start();
new Thread(() -> {
s.printABC(s2, s3);
}).start();
new Thread(() -> {
s.printABC(s3, s1);
}).start();
}
}
如果需要结束时统一打印end: Lock+Condition+CountDownLatch
// 多定义一个CountDownLatch
private static CountDownLatch cdl = new CountDownLatch(3);
// 在printABC内部循环完10次之后
cdl.countDown();
// 在main方法中,三个线程start()结束后
cdl.await();
System.out.println("END");
求最大公约数 gcd(a,b)
public int gcd(int a, int b){
return b==0? a: gcd(b, a%b);
}
ACM模式中建树建表和建图
建表
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;
public class Main_linkedList {
static class Node{
int val;
Node next;
public Node(int val){
this.val = val;
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
//输入 1 2 3 4 5
List<Integer> list = new ArrayList<>();
while(sc.hasNextInt()){
list.add(sc.nextInt());
}
int[] listNodes = new int[list.size()];
for(int i = 0; i< listNodes.length; i++){
listNodes[i] = list.get(i);
}
// 创建链表
Node dh = new Node(-1);
Node cur = dh;
for(int num : listNodes){
cur.next = new Node(num);
cur = cur.next;
}
//dh为虚拟头结点 dh.next为真正的头结点
}
}
建树
import java.util.*;
public class layerTree {
public static void main(String[] args) {
// input: [3,9,20,null,null,15,7]
Scanner scanner = new Scanner(System.in);
String str = scanner.next();
TreeNode root = buildTree(str);
List<int[]> res = new ArrayList<>();
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()){
int size = queue.size();
int[] path = new int[size];
int idx = 0;
while(size-- > 0){
TreeNode cur = queue.poll();
path[idx++] = cur.val;
if(cur.left != null){
queue.offer(cur.left);
}
if (cur.right != null){
queue.offer(cur.right);
}
}
res.add(path);
}
int[][] ans = new int[res.size()][];
for(int i = 0; i<res.size(); i++){
ans[i] = res.get(i);
}
// System.out.println(ans);
// System.out.println();
}
public static TreeNode buildTree(String str){
// root = [3,9,20,null,null,15,7]
String[] nums = str.substring(1, str.length()-1).split(",");
TreeNode root = new TreeNode(Integer.parseInt(nums[0]));
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
int idx = 1;
while(!queue.isEmpty() && idx < nums.length){
TreeNode cur = queue.poll();
if (!nums[idx].equals("null")){
cur.left = new TreeNode(Integer.parseInt(nums[idx]));
queue.offer(cur.left);
}
idx++;
if (!nums[idx].equals("null")){
cur.right = new TreeNode(Integer.parseInt(nums[idx]));
queue.offer(cur.right);
}
idx++;
}
return root;
}
static class TreeNode{
int val;
TreeNode left;
TreeNode right;
public TreeNode(){};
public TreeNode(int val){
this.val = val;
this.left = null;
this.right = null;
}
}
}
建树/图
输入:
n
n个节点的colors
n-1对u-v边
选择建为图
import java.util.*;
public class Main_color {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
String str = scanner.next();
char[] colors = str.toCharArray();
TreeGraph graph = new TreeGraph();
for(int i = 0; i<n-1; i++){
int u = scanner.nextInt();
int v = scanner.nextInt();
if (!graph.nodes.containsKey(u)){
graph.nodes.put(u, new TreeNode(u, colors[u-1]));
}
if (!graph.nodes.containsKey(v)){
graph.nodes.put(v, new TreeNode(v, colors[v-1]));
}
TreeNode father = graph.nodes.get(u);
TreeNode child = graph.nodes.get(v);
father.children.add(child);
child.children.add(father);//双向
}
TreeNode root = graph.nodes.get(1);
Queue<TreeNode> queue = new LinkedList<>();
int cnt = 0;
queue.add(root);
HashSet<TreeNode> set = new HashSet<>();
set.add(root);
while(!queue.isEmpty()){
TreeNode cur = queue.poll();
for (TreeNode next : cur.children){
if (next.color == cur.color){
cnt++;
if (cur.color == 'R'){
next.color = 'W';
}else{
next.color = 'R';
}
}
if (!set.contains(next)){
queue.offer(next);
set.add(next);
}
}
}
System.out.println(cnt);
}
public static class TreeNode{
public int id;
public char color;
public List<TreeNode> children;
public TreeNode(int i, char c){
this.id = i;
this.color = c;
children = new ArrayList<>();
}
}
public static class TreeGraph{
public HashMap<Integer, TreeNode> nodes;
public TreeGraph(){
nodes = new HashMap<>();
}
}
}
工具:IntStream、LongStream 和 DoubleStream
这三个原始流在 java.util.stream 命名空间下,并提供了大量的方法用于操作流中的数据,同时提供了相应的静态方法来初始化它们自己
创建IntStream流(IntStream中的静态方法:of / builder/ range / rangeClosed / generate / iterate)
IntStream.of()方法
IntStream intStream = IntStream.of(1);
IntStream intStream = IntStream.of(1,2,3,4,5);
IntStream.range()、IntStream.rangeClosed()方式
range():前闭后开区间;
rangeClosed():前闭后闭区间;
IntStream range = IntStream.range(1, 100); // 返回 1,2,3,4,......,99
IntStream range = IntStream.rangeClosed(1, 100); // 返回 1,2,3,4,......,99,100
IntStream.iterate()方式
根据指定规则,生成一串int流(使用iterate()方式,也是无限连续的流,需使用limit()来限制元素的数量)
// 规则:生成2的幂次方int流
IntStream intStream11 = IntStream.iterate(1,x->2 * x).limit(6);
IntStream.concat()方式 (将两个int流合并成一个流)
IntStream range1 = IntStream.range(1, 5); // A流
IntStream range2 = IntStream.range(10, 15); // B流
IntStream concat = IntStream.concat(range1, range2); // 合并后的流
filter() 方法过滤出符合条件的数据
用于过滤数据,返回符合过滤条件的数据,是一个非终结方法
可以通过 filter() 方法将一个流转换成另一个子集流。该接口接收一个 Predicate 函数式接口参数(可以是一个 Lambda 或 方法引用) 作为筛选条件。因为 filter() 是一个非终结方法,所以必须调用终止方法。
// 获取1-9的int流
IntStream intStream = IntStream.range(1, 10);
// 通过filter方式过滤掉小于5的数字,并输出
intStream.filter(x->x>5).forEach(System.out::println);
map()方法对流中所有元素执行某个修改操作
IntStream 中的map()方法用于对流中的所有元素执行某个修改操作,这与 Stream 中的map()方法有所不同
IntStream intStream = IntStream.range(1, 10);
intStream.map(o -> 2 * o).forEach(System.out::println);
mapToObj / mapToLong / mapToDouble / asLongStream / asDoubleStream
1.mapToObj:将 int 流转换成其他类型的流 (其他类型:可以使自定义对象类型,也可以是List类型等)
2.mapToLong:将 int 流转换成Long类型的流,不可指定返回值规则
3.mapToDouble:将 int 流转换成Double类型的流,不可指定返回值规则
4.asLongStream:将 int 流转换成Long类型的流,该方法遵循标准的int到指定类型的转换规则,不能指定规则,比如说将int流对象先 乘以2再返回
5.asDoubleStream:将 int 流转换成Double类型的流,该方法遵循标准的int到指定类型的转换规则,不能指定规则,比如说将int流对象先 乘以2再返回
IntStream intStream = IntStream.range(1, 10);
// mapToObj():将int流转换成Person对象
intStream.mapToObj(val -> new Person(val, "Mary" + val))
.forEach(System.out::println);
IntStream intStream = IntStream.range(1, 10);
// mapToLong()方法(可指定返回值规则)
intStream.mapToLong(val -> 2 * val).forEach(System.out::println);
// mapToDouble()方法(可指定返回值规则)
intStream.mapToDouble(val -> 2 * val).forEach(System.out::println);
// asDoubleStream()方法(不可指定返回值规则)
intStream.asDoubleStream().forEach(System.out::println);
// asLongStream()方法(不可指定返回值规则)
intStream.asLongStream().forEach(System.out::println);
forEach / forEachOrdered
用来遍历流中的元素,是一个终结方法
1.forEach:遍历流中的元素
2.forEachOrdered:forEachOrdered同forEach的区别在于并行流处理下,forEachOrdered会保证实际的处理顺序与流中元素的顺序一致,而forEach方法无法保证,默认的串行流处理下,两者无区别,都能保证处理顺序与流中元素顺序一致。
IntStream intStream = IntStream.of(2,6,3,5,9,8,1);
intStream.forEach(x->{
System.out.println("forEach->"+x);
});
distinct()方法
可以用来去除重复数据。因为 distinct() 方法是一个非终结方法,所以必须调用终止方法
IntStream intStream = IntStream.of(1, 2, 3, 4, 5, 6, 1, 4, 5, 2);
intStream.distinct().forEach(System.out::println);
sorted() 方法
用来对 Stream 流中的数据进行排序
Stream流中的sorted()方法,还允许我们自定义Comparator规则进行排序;参考:JDK8新特性(三):集合之 Stream 流式操作 中的sorted()方法
IntStream流中的sorted()方法,就是纯粹对int数值进行排序,所以也没有Comparator自定义比较器排序的必要
IntStream.of(nums)
.boxed() //转为Stream流
.sorted((o1, o2) -> Math.abs(o2) - Math.abs(o1))
skip
如果希望跳过前几个元素,去取后面的元素,则可以使用 skip()方法,获取一个截取之后的新流,它是一个非终结方法。参数是一个 long 型,如果 Stream 流的当前长度大于 n,则跳过前 n 个,否则将会得到一个长度为 0 的空流。因为 limit() 是一个非终结方法,所以必须调用终止方法。
IntStream intStream = IntStream.of(1, 9, 4, 35, 5, 2);
// skip()跳过流中前2个元素,获取剩下的元素
intStream.skip(2).forEach(System.out::println);
sum / min / max / count / average / summaryStatistics
sum:求和
min:求最小值
max:求最大值
count:计算IntStream流中元素个数
average:求平均值
summaryStatistics:该方法一次调用获取上述5个属性值
boxed()
boxed:翻译过来是盒子被包装的意思。即:返回由IntStream流中的元素组成的Stream流,每个box 都装着Integer类
在Stream流中,是没有boxed()方法的;
只有在IntStream、DoubleStream、LongStream 这三种类型的流中,才有boxed()方法
// 1.通过mapToObj()方法的方式返回Stream<xxx>类型
IntStream intStream = IntStream.of(1, 9, 4, 35, 5, 2);
intStream.mapToObj(Integer::valueOf).collect(Collectors.toList()).forEach(System.out::println);
// 2.通过boxed()方法的方式返回Stream<Integer>类型
IntStream intStream1 = IntStream.of(1, 9, 4, 35, 5, 2);
Stream<Integer> boxed = intStream1.boxed(); // 看这里,通过boxed返回的是Stream<Integer>类型
List<Integer> collect = boxed.collect(Collectors.toList()); // 转换成List<Integer>类型
//3.通过mapToInt()方法把Stream流转IntStream
boxed.mapToInt(Integer::intValue)
toArray()
将IntStream流中的元素转换成一个数组
IntStream intStream = IntStream.of(1, 9, 4, 35, 5, 2);
// toArray:将IntStream流中的元素转换成一个数组
int[] intArray = intStream.toArray();
例子
将数组按照绝对值大小从大到小排序
int[] nums = {4,-2,3,-9,1};
nums = IntStream.of(nums).boxed().sorted((o1,o2)-> Math.abs(o2)- Math.abs(o1))
.mapToInt(Integer::intValue).toArray();