1 问题描述
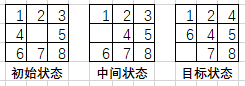
3×3九宫棋盘,放置数码为1-8的8个棋牌,剩下一个空格,只能通过棋牌向空格的移动来改变棋盘的布局。要求:根据给定初始布局(即初始状态)和目标布局(即目标状态),如何移动棋牌才能从初始布局到达目标布局,找到合法的走步序列。
图1 求解过程示例
2 求解算法设计
2.1算法原理分析
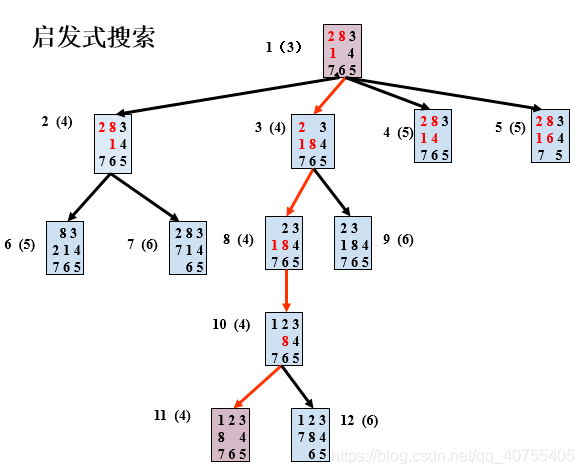
本次实验采用了启发式搜索算法来求解八数码问题。其基本思想是从根节点拓展出子节点,然后从所有未拓展过的节点中选出代价最小的节点,并拓展该节点。然后继续从所有未拓展过的节点中选出代价最小的节点并拓展,循环调用这个步骤直到找到目标节点。
启发函数h(n):当前节点与目标节点格局相比,位置不符的数字移动到目标节点中对应位置的最短距离之和。
图2 全局择优搜索过程示例
2.2算法步骤设计
○1读取初始状态和目标状态,并判断二者能否通过变换到达。
○2将初始节点压入OPEN表
○3取出OPEN表中估计值最小的节点,并放入CLOSE表
○4如果该节点不是目标节点,扩展该节点,将子节点放入OPEN表,并返回到第三步。
○5将该节点压入栈中,并将指针指向其父节点。
○6如果该节点的父节点不为空,返回到第五步。
○7如果栈不为空,出栈并输出该节点,直到栈为空。
#include<queue>
#include<iostream>
#include "stdlib.h"
#include "time.h"
#include<stack>
using namespace std;
#define num 9
struct Node{
int state[9];
struct Node* parent;
int value;
int depth;
friend bool operator < (Node A, Node B) //按照value值小的方案构造优先级队列
{
return A.value > B.value;
}
};
priority_queue<Node> openTable; //open表
queue<Node> closeTable; //close表
stack<Node> Path; //最终路径
int count1=0,count2=0;
int read(Node& S,Node& G){
/*初始化*/
S.parent=NULL; S.depth=0; S.value=0;
G.parent=NULL; G.depth=0; G.value=0;
cout<<"请输入初始状态\n";
for(int i=0;i<num;i++)
cin>>S.state[i];
cout<<"请输入目标状态?\n";
for(int i=0;i<num;i++)
cin>>G.state[i];
for(int i=0;i<=num-2;i++)
for(int j=i+1;j<num;j++)
if(S.state[i]>S.state[j]&&S.state[i]*S.state[j]!=0)
count1++;
for(int i=0;i<=num-2;i++)
for(int j=i+1;j<num;j++)
if(G.state[i]>G.state[j]&&G.state[i]*G.state[j]!=0)
count2++;
if(count1%2!=count2%2)
{
return 0;
}
return 1;
}
int value1(Node A,Node G){
int count=8;
for(int i=0;i<num;i++)
if(A.state[i]==G.state[i]&&G.state[i]!=0)
count--;
return count +A.depth;
}
int value2(Node A,Node G){
int count=0,begin[3][3],end[3][3]; //count记录所有棋子移动到正确位置需要的步数
for(int i = 0; i < num; i++){
begin[i/3][i%3]=A.state[i];
end[i/3][i%3]=G.state[i];
}
for(int i = 0; i < 3; i++) //检查当前图形的正确度
for(int j = 0; j < 3; j++)
{
if(begin[i][j] == 0)
continue;
else if(begin[i][j] != end[i][j])
{
for(int k=0; k<3; k++)
for(int w=0; w<3; w++)
if(begin[i][j] == end[k][w])
count = count + fabs(i-k*1.0) + fabs(j-w*1.0);
}
}
return count +A.depth;
}
bool judge(Node S, Node G)
{
for (int i = 0; i <= 8; i++)
{
if (S.state[i] != G.state[i])
{
return false;
}
}
return true;
}
//产生新节点,加入OPEN表
void creatNode(Node& S, Node G)
{
/* 计算原状态下,空格所在的行列数,从而判断空格可以往哪个方向移动 */
int blank; //定义空格下标
for(blank=0;blank<9&&S.state[blank]!=0;blank++) ;//找到空白格
int x =blank / 3, y = blank % 3; //获取空格所在行列编号
for (int d = 0; d < 4; d++) //找到S扩展的子节点,加入open表中
{
int newX=x,newY=y;//新空白格坐标
Node tempNode;
/*移动空白格*/
if(d==0) newX = x -1;
if(d==1) newY = y -1;
if(d==2) newX = x +1;
if(d==3) newY = y +1;
int newBlank = newX * 3 + newY; //空格新的位置
if (newX >= 0 && newX < 3 && newY >= 0 && newY < 3) //如果移动合法
{
/* 交换新旧空白格的内容*/
tempNode = S;
tempNode.state[blank] = S.state[newBlank];
tempNode.state[newBlank] =0;
if ( S.parent!=NULL&&(*S.parent).state[newBlank] == 0) //如果新节点和爷爷节点一样,舍弃该节点
{
continue;
}
/* 把子节点都加入open表中 */
tempNode.parent = &S;
tempNode.value = value2(tempNode, G);
tempNode.depth = S.depth + 1;
openTable.push(tempNode);
}
}
}
int main()
{
Node S0,Sg;
if(!read(S0,Sg))
{cout<<"两点之间不可达!";
system("pause");
return 0;
}
clock_t start, finish;
start = clock();
openTable.push(S0);
while (true)
{
closeTable.push(openTable.top()); //将open表中优先级最高的元素压入close表中
openTable.pop(); //剔除open表中优先级最高的元素
if (!judge(closeTable.back(), Sg)) //如果当前棋局与目标棋局不相同,则拓展当前节点
{
creatNode(closeTable.back(), Sg);
}
else
{
break;
}
}
Node tempNode; //临时变量暂存队前数据
tempNode = closeTable.back();
while (tempNode.parent != NULL)
{
Path.push(tempNode);//压入
tempNode = *(tempNode.parent);//指向父节点
}
Path.push(tempNode);
cout << "至少要移动" << Path.size() - 1 << "步" << endl;
/* 输出方案 */
while (Path.size() != 0)
{
for (int i = 0; i <= 8; i++)
{
cout << Path.top().state[i]<<" ";
if((i+1)%3==0)
cout <<endl;
}
Path.pop();
cout << "\n";
}
finish = clock();
cout<< (finish-start )<<"毫秒";
system("pause");
return 0;
}
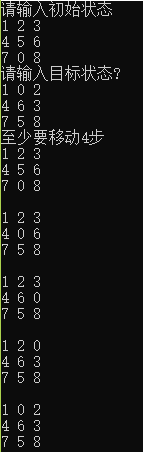
运行结果如下: