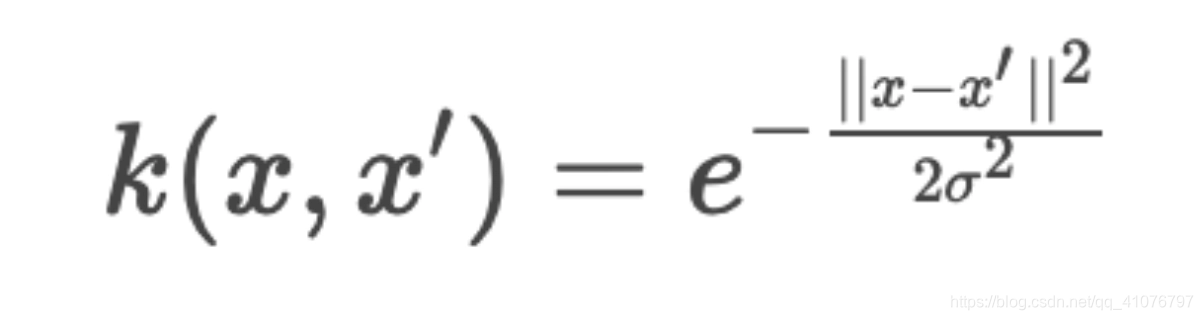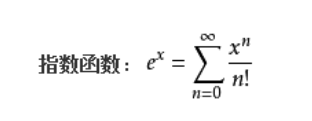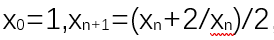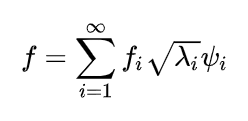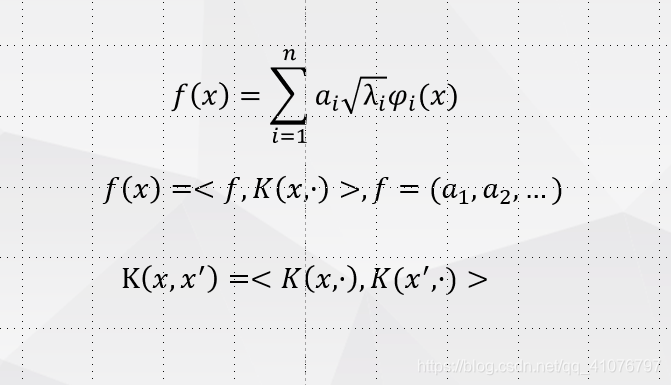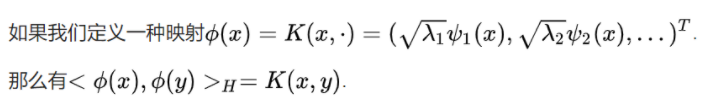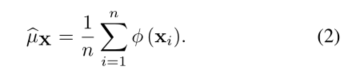目录
核函数是用来干嘛的?
- 核函数能对低维数据进行某种低成本的运算使得运算结果等于高维空间映射函数的内积。
- 即给我两个低维空间样本
x
x
x,
x
′
x'
x′,映射函数
ϕ
(
x
)
ϕ(x)
ϕ(x),那么
k ( x , x ′ ) = < ϕ ( x ) , ϕ ( x ′ ) > k(x,x')=<ϕ(x),ϕ(x')> k(x,x′)=<ϕ(x),ϕ(x′)>,其中 ϕ ( x ) ϕ(x) ϕ(x)是映射到高维空间的函数向量。
为什么非要在高维空间计算内积?
- 有具体的应用场景,比如二维下线性不可分的两种分布在高维下才能区分开,而这就涉及高维空间的内积运算,而计算高维空间甚至无限维空间的两组向量的内积成本更高。
- 举个栗子
注意,这里的 ψ ψ ψ和 f f f都是映射函数,而不是下面讲的正交基底。 - 在我看来,上面那个例子只是一个表现,更根本的原因是需要用向量内积来表示两个向量的相似性。在支持向量机中我们都知道有一个高斯核函数,它对应的映射函数恰好可以映射到无穷维上,映射到无穷维上再求期望,正好可以得到随机变量的高阶矩,这个方法有一个更高大上的名字,叫做kernel embedding of distributions,这个简单理解就是将一个分布映射到再生希尔伯特空间(每个核函数都对应一个RKHS)上的一个点,这个点与原点可以构成一个向量,也就是说,任意一个分布都可以用一个向量来表示,所以描述两个分布的差异(相似度),就可以用两个点的向量的向量内积来表示。
- 但是这里面其实有一个问题,那就是,向量内积ab=|a||b|cosθ,也就是说只有在归一化的情况下,才能用内积表示相似度。我们在这里并没有进行归一化,是无法用向量来表示相似度的,不然相似度的取值(即向量内积的取值)值域就是一个无穷大的区间。换句话说,向量内积涵盖了模长和向量夹角,而相似度应当是单独研究模长或者是角度,故而,这里需要添加一个约束。这个约束就是 ∣ ∣ f ∣ ∣ H ||f||_H ∣∣f∣∣H<=1,以三维空间距离,就是点全部在一个球体内,但是由于我们的目标是最大化(后面会提到),所以取 ∣ ∣ f ∣ ∣ H ||f||_H ∣∣f∣∣H=1,也就是每个映射到三维空间的点,都让它们分布在三维球体表面,这样就相当于模长固定为1了,可以使用向量内积来进行相似度的评价了。
提到的映射函数是什么意思?与核函数有什么关系?
- 首先二者没有关系,如果非要说有,那就是同事关系,同时参与这件事情,并相互影响但不是决定性的,举个栗子。
- 假设现在存在一个映射函数f(x,y),它能将二维向量映射到三维空间,那你说映射函数转化为向量是几维?当然是三维啦!假设表达式如下:
f ( x , y ) = ( x 2 , 2 x y , y 2 ) f(x,y)=(x^2,\sqrt2xy,y^2) f(x,y)=(x2,2xy,y2)
假设二维空间下的两个样本 u = ( x 1 , y 1 ) u=(x1,y1) u=(x1,y1)和 v = ( x 2 , y 2 ) v=(x2,y2) v=(x2,y2),那么计算映射函数的内积如下:
< f ( x 1 ) , f ( x 2 ) > = < ( x 1 2 , 2 x 1 y 1 , y 1 2 ) , ( x 2 2 , 2 x 2 y 2 , y 2 2 ) > = x 1 2 x 2 2 + 2 x 1 2 x 2 2 y 1 2 y 2 2 + y 1 2 y 2 2 = ( x 1 x 2 + y 1 y 2 ) 2 = < u , v > 2 <f(x1),f(x2)>=<(x_1^2,\sqrt2 x_1y_1,y^2_1),(x_2^2,\sqrt2 x_2y_2,y^2_2)>=x_1^2x_2^2+2x_1^2x_2^2y_1^2y_2^2+y_1^2y_2^2=(x_1x_2+y_1y_2)^2=<u,v>^2 <f(x1),f(x2)>=<(x12,2x1y1,y12),(x22,2x2y2,y22)>=x12x22+2x12x22y12y22+y12y22=(x1x2+y1y2)2=<u,v>2
我们可以看到,高维空间的内积可以用低维空间下样本的内积然后平方来计算,看上去好像没有省多少力气,这是因为例子里是3维,假如是无穷维的话你就知道有多省力气了。 - 所以这里设置核函数 K ( p 1 , p 2 ) = < p 1 , p 2 > 2 K(p1,p2)=<p1,p2>^2 K(p1,p2)=<p1,p2>2,其中 p i = ( x i , y i ) p_i=(x_i,y_i) pi=(xi,yi)表示二维空间样本。
- 一般我们是先确定核函数的,要知道每一个核函数都隐式地定义了一个特征映射函数:
高斯核函数是如何映射到无限维度的?
- 首先附上高斯核函数公式:
假设 σ = 1 / 2 σ=1/\sqrt 2 σ=1/2,这么假设的意思就是使分母为1方便表示,这个参数对于讲解本问题无关紧要。 - 下面看图:
第三步使用了泰勒公式:
同时在推导的最后一行我们也看到了向量形式的映射函数,维度是无穷大,给它一个样本 [ 1 , 特 征 维 度 ] [1,特征维度] [1,特征维度]就会返回由无穷维度的映射函数得到的无穷维度向量,它就是低维样本映射到无穷维空间的点。
一个函数成为核函数的条件
函数基
- 先了解一下函数基的知识:
可以看出,函数可以化为向量的形式,而向量是可以用基来线性表示的,基的维度和空间维度相同。
其他
- 满足以下两个条件:
- K ( x , y ) = K ( y , x ) K(x,y)=K(y,x) K(x,y)=K(y,x)
- ∫ f ( x ) K ( x , y ) f ( y ) d x d y > = 0 , f \int f(x)K(x,y)f(y)dxdy>=0,f ∫f(x)K(x,y)f(y)dxdy>=0,f为任意函数
- 条件2其实就是证明矩阵为半正定矩阵的条件,其中K是无穷维矩阵,f是无穷维向量,条件2的另一种表述是K对应的Gram矩阵为半正定的。参考下图:
可以把核函数看成是一个二维无穷大矩阵,类比于矩阵的特征分解,可以找到一组特征值及其对应的特征函数,这些特征函数作为一组正交基可以构成一个函数空间。 无穷大是指样本空间应该是无穷大的,这里用n表示样本数量。
该gram矩阵是半正定即可。 - 怎么判断正定性?先来了解一下矩阵的特征值分解:
不是每一个矩阵都可以分解成特征值和特征向量。在某些情况下,特征分解存在,但是会涉及复数而非实数。具体来讲,每个实对称矩阵都可以分解成实特征向量和实特征值,很明显gram矩阵是实对称矩阵。 - 所有特征值都是正数的矩阵被称为正定(positive definite);所有特征值都是非 负数的矩阵被称为半正定(positive semidefinite)。同样地,所有特征值都是负数的矩阵被称为负定(negative definite);所有特征值都是非正数的矩阵被称为半负定(negative semidefinite)。
- 核函数矩阵gram也可以进行特征值分解:
离散时,上式的 j j j就取到 n n n,否则就是 ∞ ∞ ∞。 - 有了矩阵就可以判断正定性了。
- 现在我们思考,给出10个2维的样本,我们可以构造出一个10x10的gram矩阵,由于gram的实对称性,一定可以进行特征分解,对于值固定的矩阵gram,就一定有固定值的特征向量与之形成下面的公式:
即,一定有值固定的正交基,但是请注意,麻烦就麻烦在,gram矩阵的值是核函数值,一个矩阵的值都不是一个定值,而是一个函数,核函数。所以导致,x,y值与核函数输出值相联系,而核函数输出值与gram矩阵的正交基分量值相联系,从而得出—— x , y x,y x,y值与正交基值相联系,即正交基的值其实是一个与x,y值相联系的函数,换化为函数形式,称之为特征函数,就得到了正交向量组。先不要管怎么求这个特征函数,总之一定存在。
本来普通矩阵建立的关系式是:
A i j = ∑ k = 1 n λ k q k i q k j A_{ij}=\displaystyle\sum_{k=1}^n λ_kq_{ki}q_{kj} Aij=k=1∑nλkqkiqkj, q q q是实实在在的向量,值是实数。
因为gram的特殊,导致:
K ( x , y ) = ∑ i = 1 ∞ λ i ψ i ( x ) ψ i ( y ) K(x,y)=\displaystyle\sum ^∞_{i=1} λ_iψ_i(x)ψ_i(y) K(x,y)=i=1∑∞λiψi(x)ψi(y) - 怎么理解上面这个式子,可以从两个角度,首先是矩阵:
因为我们要引入 x , y x,y x,y,所以没有下标 i j ij ij,那你可能会问,为啥不将样本都编码,依然用下标表示呢?因为只要样本确定了,矩阵就确定了,那特征向量就确定了,剩下的只是表示的问题。 - 不要忘了, 样本是无限的,矩阵 K K K是无穷维的!根本不存在 K 11 K_{11} K11这种意义,任何一个点都不敢说是在矩阵的任意一个顶点上,根本无法用下标表示。要确定一个点,只能通过给定 x x x和 y y y的值,所以 ψ i ( x ) ψ_i(x) ψi(x)和 ψ i ( y ) ψ_i(y) ψi(y)表示告诉特征函数取哪个值相乘,就好比 q k i q_{ki} qki,它可以用下标 i i i来告诉特征向量,而我们只能用样本去告诉特征函数,它内部建立了样本到数值的映射,所以说是个函数基底。 ψ i ψ_i ψi不再是实数向量,而是函数向量,根据 x x x的不同,取出向量对应的分量值。
- 其实说白了,就是从这里根据x取值从向量分量中挑一个:
- 这里有必要交代一下,这里的 ψ i ψ_i ψi代表的是函数正交基底,不能和映射函数混了!虽然使用同样的符号。对于无穷矩阵 K K K来说,基底可能是永远无法得知的,但我们应该知道是有这么个东西存在的。
- 从空间角度:
首先核函数是将两个样本映射到了无限维的希尔伯特空间,空间的基底是函数基底,也就是说,空间内任何一个函数都可以由函数基底的线性组合来表示,核函数映射两个样本的两个希尔伯特空间的函数也不例外。见下图:
红色和蓝色两个希尔伯特空间函数就是映射的结果,它们都能被函数基底线性表示:
蓝 色 = ∑ i = 1 ∞ λ i ψ i ( x ) 蓝色=\displaystyle\sum _{i=1}^∞ λ_iψ_i(x) 蓝色=i=1∑∞λiψi(x)、 红 色 = ∑ i = 1 ∞ λ i ψ i ( y ) 红色=\displaystyle\sum _{i=1}^∞ λ_iψ_i(y) 红色=i=1∑∞λiψi(y)
而我们知道 K ( x , y ) = < 蓝 色 , 红 色 > H K(x,y)=<蓝色,红色>_H K(x,y)=<蓝色,红色>H
所以,得到上式
K ( x , y ) = ∑ i = 1 ∞ λ i ψ i ( x ) ψ i ( y ) K(x,y)=\displaystyle\sum ^∞_{i=1} λ_iψ_i(x)ψ_i(y) K(x,y)=i=1∑∞λiψi(x)ψi(y) - 连续时满足条件才能说这个函数是核函数。
- 这里再讲一下对称性,即第一个条件。连续时对称性:
同时类比离散时矩阵特征值分解时的结论:
和离散时一样, { ψ i } i = 1 ∞ \{ψ_i\}_{i=1}^{∞} {ψi}i=1∞是一组正交基。 ψ i ψ_i ψi应被看做是函数转化的无穷向量。
核函数与再生核希尔伯特空间的关系
希尔伯特空间
- 首先明确一下什么是希尔伯特空间,完备的定义了内积的线性空间就是希尔伯特空间。
- 内积空间=线性空间+内积,所以希尔伯特空间=内积空间+完备性。
- 完备空间或者完备度量空间是具有下述性质的空间:空间中的任何柯西序列都收敛在该空间之内。
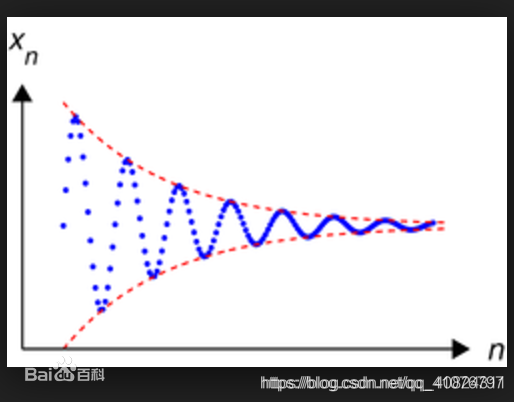
- 一个柯西序列是指一个这样一个序列,它的元素随着序数的增加而愈发靠近,如下图所示:
- 以复数序列为例,设复数序列(z1,z2,z3…),若该序列为柯西列,那么对于任何正实数r>0,存在正整数N使得所有整数m,n≥N,都有|zm-zn|<r,其中竖线表示绝对值或模。
为了将柯西列的定义推广到一般的度量空间,可将绝对值替换为该度量空间的距离(实际上|zm-zn|也是一种度量空间中的距离),那么上述表示可更改为:设复数序列(z1,z2,z3…),若该序列为柯西列,那么对于任何正实数r>0,存在正整数N使得所有整数m,n≥N,都有d(zm,zn)<r,其中d(zm,zn)表示zm和zn之间的距离。
可以看出柯西列的定义依赖于距离的定义,只有在度量空间中柯西列才有意义,因此一些场合中完备空间也被称为完备度量空间;另外根据完备空间的定义,也可将完备空间称为柯西空间。 - 而内积空间是在线性空间中加入了内积运算,而且,内积空间具有基于空间本身的内积所自然定义的范数,, 且其满足平行四边形定理,也就是说内积可以诱导一个范数,所以内积空间一定是“赋范空间”。而又因为在向量空间中,范数可以诱导距离(或称“度量”),反之不成立,这也意味着赋范空间一定属于度量空间;所以说内积空间一定是个度量空间,那么就一定包含距离的定义,所以具有柯西的依赖条件。
- 总结来说:
向量空间+范数运算=(线性)赋范空间
(线性)赋范空间+内积运算=内积空间
(线性)赋范空间+完备性=巴拿赫空间
内积空间+完备性+有限维=欧几里德空间
内积空间+完备性=希尔伯特空间
- 举个空间不完备的例子:
在以绝对值为范数的有理数空间中,定义序列:
该序列是柯西序列,但该序列收敛到√2,可以看到收敛值并不在该有理数空间,那么该有理数空间不是完备的。
直观上讲,一个空间完备就是指“没有孔”且“不缺皮”,两者都是某种“不缺点”。没有孔是指内部不缺点,不缺皮是指边界上不缺点。
最后注意收敛序列一定是柯西序列,但柯西序列并一定收敛,只有在完备度量空间下柯西序列才是收敛的,例如上面的证明有理数不完备时构造的数组,该数组收敛到√2,但√2并不是有理数,那么在该有理数空间中,该数组虽然是柯西序列,但并不收敛。 - 所以希尔伯特空间定义的流程是:
线性空间(向量空间)–> 内积空间 –> 赋范向量空间 –> 度量空间 –完备的–> 希尔伯特空间 - 另外,希尔伯特空间是一个函数空间,即空间中每个元素都是一个函数。如果你理解了MMD的核技巧应该也能自己发现这个特性。给你一个映射到无穷维度的核函数,对于样本空间的任意两点的,输入到核函数进行计算,结果都等于无穷维度两个无穷向量的内积。而样本空间无穷的话,核函数转化为矩阵就是无穷大的,对应的特征向量维度和特征值数量就都是无穷大的,而且形成的空间也是连续的,以特征向量为基底可以表示空间里任意一个向量。这个连续的空间,就是希尔伯特空间。
再生希尔伯特空间
- 再生核希尔伯特空间使用的是固定的
{
λ
i
ψ
i
}
i
=
1
∞
\{\sqrt{λ_i}ψ_i\}^∞_{i=1}
{λiψi}i=1∞作为正交基,这个空间中任何一个函数(向量)都可以表示为这组正交基的线性组合。
即
因此 f f f可以表示成 f = ( f 1 , f 2 , … ) H T f=(f_1,f_2,…)^T_H f=(f1,f2,…)HT, - 我们前面说过
K ( x , y ) = ∑ i = 1 ∞ λ i ψ i ( x ) ψ i ( y ) K(x,y)=\displaystyle\sum ^∞_{i=1} λ_iψ_i(x)ψ_i(y) K(x,y)=i=1∑∞λiψi(x)ψi(y)
这个式子输入具体样本 x 0 , y 0 x_0,y_0 x0,y0后得到的是一个标量,也就是说可以表示成如下两个向量的内积
[ λ 1 ψ 1 ( x 0 ) , λ 2 ψ 2 ( x 0 ) , . . . ] [\sqrt{λ_1}ψ_1(x_0),\sqrt{λ_2}ψ_2(x_0),...] [λ1ψ1(x0),λ2ψ2(x0),...]、 [ λ 1 ψ 1 ( y 0 ) , λ 2 ψ 2 ( y 0 ) , . . . ] [\sqrt{λ_1}ψ_1(y_0),\sqrt{λ_2}ψ_2(y_0),...] [λ1ψ1(y0),λ2ψ2(y0),...]
倘若我们固定一个自变量(比如x),让另一个自变量是未知的(比如y),那就变成了:
[ λ 1 ψ 1 ( x 0 ) , λ 2 ψ 2 ( x 0 ) , . . . ] [\sqrt{λ_1}ψ_1(x_0),\sqrt{λ_2}ψ_2(x_0),...] [λ1ψ1(x0),λ2ψ2(x0),...]、 [ λ 1 ψ 1 , λ 2 ψ 2 , . . . ] [\sqrt{λ_1}ψ_1,\sqrt{λ_2}ψ_2,...] [λ1ψ1,λ2ψ2,...]是的,第二个向量的分量是一个函数,取值取决于自变量,也就是正交函数基底。
即
K ( x , ⋅ ) = ∑ i = 1 ∞ λ i ψ i ( x ) ψ i = < [ λ 1 ψ 1 ( x 0 ) , λ 2 ψ 2 ( x 0 ) , . . . ] , [ λ 1 ψ 1 , λ 2 ψ 2 , . . . ] > K(x,·)=\displaystyle\sum ^∞_{i=1} λ_iψ_i(x)ψ_i=<[\sqrt{λ_1}ψ_1(x_0),\sqrt{λ_2}ψ_2(x_0),...],[\sqrt{λ_1}ψ_1,\sqrt{λ_2}ψ_2,...]> K(x,⋅)=i=1∑∞λiψi(x)ψi=<[λ1ψ1(x0),λ2ψ2(x0),...],[λ1ψ1,λ2ψ2,...]>
这相当于只关心无穷矩阵 K ( x , y ) K(x,y) K(x,y)的任意一行,想取哪一行就让x等于几,这只影响 ψ i ( x ) ψ_i(x) ψi(x)的值,后面的 ψ i ψ_i ψi是 y y y取所有可能,对应的无穷维向量。
x x x取 x 0 x_0 x0,那么
K ( x 0 , y ) = ∑ i = 1 ∞ λ i ψ i ( x 0 ) ψ i K(x_0,y)=\displaystyle\sum ^∞_{i=1} λ_iψ_i(x_0)ψ_i K(x0,y)=i=1∑∞λiψi(x0)ψi
可以这么想, x 0 x_0 x0固定了,那就是固定了矩阵的 x 0 x_0 x0这一行,然后遍历该行所有列,其实就是让样本 x 0 x_0 x0与其他所有样本求核函数值 k ( x 0 , y ) k(x_0,y) k(x0,y)。 x 0 x_0 x0固定的直接影响就是第一个 ψ i ψ_i ψi只取 x 0 x_0 x0对应的分量。
然后由于基底是 { λ i ψ i } i = 1 ∞ \{\sqrt{λ_i}ψ_i\}^∞_{i=1} {λiψi}i=1∞
所以将函数转化为向量表达式就成了:
K ( x , ⋅ ) = ( λ 1 ψ 1 ( x ) , λ 2 ψ 2 ( x ) , … … ) H T K(x,·)=(\sqrt {λ_1}ψ_1(x),\sqrt {λ_2}ψ_2(x),……)_H^T K(x,⋅)=(λ1ψ1(x),λ2ψ2(x),……)HT
为啥转化成这样?参考下图:
要记住,这里的自变量还是 x x x哈,对于每一个 x x x, y y y取无穷列,所以 K ( x , ⋅ ) K(x,·) K(x,⋅)才是无穷维度的向量。
说白了,固定y遍历无穷列,然后 x x x只取某个值,那核函数得到的结果就是一个根据自变量 x x x变化的无穷维函数,放到再生希尔伯特空间,由于取了固定的基底 { λ i ψ i } i = 1 ∞ \{\sqrt{λ_i}ψ_i\}^∞_{i=1} {λiψi}i=1∞,变化成向量形式就是上面的式子。 - 下面从定义角度说明再生性:
- 在希尔伯特空间的基础上我们引入再生核希尔伯特空间。引入再生核的概念:在一定条件下,我们可以找到一个对应于这个Hilbert Space上的唯一的一个再生核函数
K
K
K,它满足:
- 对任意固定 x 0 x_0 x0属于 X X X, K ( x , x 0 ) K(x,x_0) K(x,x0)作为 x x x的函数都属于 H H H
- 对任意 x x x属于 X X X和 f ( ⋅ ) f(·) f(⋅)属于 H H H,有 f ( x ) = < f ( ⋅ ) , K ( ⋅ , x ) > H f(x)=<f(·),K(·,x)>_H f(x)=<f(⋅),K(⋅,x)>H,这是再生性。
- 则称 K ( x , y ) K(x,y) K(x,y)为 H H H的再生核, H H H是以 K ( x , y ) K(x,y) K(x,y)为再生核的Hilbert空间,简称再生核Hilbert空间,简记为RKHS(Reproducing Kernel Hilbert Space)。
- 关于再生性,前面我们讲过
K ( x , y ) = K ( x , ⋅ ) = ( λ 1 ψ 1 ( x ) , λ 2 ψ 2 ( x ) , … … ) H T K(x,y)=K(x,·)=(\sqrt {λ_1}ψ_1(x),\sqrt {λ_2}ψ_2(x),……)_H^T K(x,y)=K(x,⋅)=(λ1ψ1(x),λ2ψ2(x),……)HT
同理有
K ( x , y ) = K ( y , ⋅ ) = ( λ 1 ψ 1 ( y ) , λ 2 ψ 2 ( y ) , … … ) H T K(x,y)=K(y,·)=(\sqrt {λ_1}ψ_1(y),\sqrt {λ_2}ψ_2(y),……)_H^T K(x,y)=K(y,⋅)=(λ1ψ1(y),λ2ψ2(y),……)HT
所以,有
< K ( x , ⋅ ) , K ( y , ⋅ ) > H = ∑ i = 1 ∞ λ i ψ i ( x ) ψ i ( y ) T = K ( x , y ) <K(x,·),K(y,·)>_H=\displaystyle\sum ^∞_{i=1} λ_iψ_i(x)ψ_i(y)^T=K(x,y) <K(x,⋅),K(y,⋅)>H=i=1∑∞λiψi(x)ψi(y)T=K(x,y)
这是从核函数的角度去描述再生核希尔伯特空间的再生性,即用核函数来再生两个高维函数向量的内积。 - 更详细的说:下面讲一下什么是再生性,设f(x)是再生核希尔伯特空间的函数,那么它一定满足第一行这个公式的定义,注意,公式最后的两部分是基底。我们可以看到,只要给出具体的确定的样本,那么基底的值就是一个确定的实数了。那有没有一点眼熟呢,对,第一行的式子在给出具体样本的时候就可以化为第二行的式子。他可以将系数和自变量完全剥离。
这还没完,更有意思的是,如果两个自变量样本都是确定的,那么还可以得到第三行的式子。
用核函数来再生两个高维函数向量的内积。这就是再生性。 - 再生性有什么用呢?
这里的映射就是映射函数了。可以看到映射函数其实就是 K ( x , ⋅ ) K(x,·) K(x,⋅),果然知识都是有联系的。现在就能够看出再生核希尔伯特空间选择这组特殊的基底到底有什么用了。 - 至于对任意
x
x
x属于
X
X
X和
f
(
⋅
)
f(·)
f(⋅)属于
H
H
H,有
f
(
x
)
=
<
f
(
⋅
)
,
K
(
⋅
,
x
)
>
H
f(x)=<f(·),K(·,x)>_H
f(x)=<f(⋅),K(⋅,x)>H是啥意思呢?看下面的式:
你可以不知道k(x,·)具体是什么,但是一定存在,或者说一定存在这么一个映射函数,使得 f ( x ) = < f ( ⋅ ) , K ( ⋅ , x ) > H f(x)=<f(·),K(·,x)>_H f(x)=<f(⋅),K(⋅,x)>H成立。 - 补充一下,其实:
这里提到的映射就是kernel embedding,而结合核函数在MMD中的应用,其实,MMD可以表示为: D H ( P , Q ) 2 = ∣ ∣ μ s ( P ) − μ t ( Q ) ∣ ∣ 2 D_H(P,Q)^2=||μ_s(P)-μ_t(Q)||^2 DH(P,Q)2=∣∣μs(P)−μt(Q)∣∣2之所以都平方是因为利用kernel trick凑内积,从而用核函数代替内积计算。其中μ是kernel embedding的无偏估计:
参考网址
- https://www.zhihu.com/question/28978098
- https://blog.csdn.net/weixin_35015064/article/details/112219269
- https://blog.csdn.net/qq_40824311/article/details/102470627
- https://blog.csdn.net/haolexiao/article/details/72171523
- https://blog.csdn.net/zkq_1986/article/details/52448238
- http://www.fanyeong.com/2017/11/13/linear-space-to-rkhs/
- https://blog.csdn.net/lyxleft/article/details/84864791
- https://zhuanlan.zhihu.com/p/363788364
- https://blog.csdn.net/sinat_40624829/article/details/100894160
- https://www.bilibili.com/read/cv11576654
- https://www.cnblogs.com/zhangcn/p/13726708.html
- https://www.zhihu.com/question/35602879
- https://zhidao.baidu.com/question/937619318484426372.html
- https://www.zhihu.com/question/24627666