自下而上的语法分析过程

一、基本思想

• 从输入串开始，朝着文法的开始符号进行最左归约， 直到到达文法的开始符号为止。主要是进行移进或归约操作，采用最左归约。

二、基本过程

• 从输入串开始，朝着文法的开始符号进行归约，直到 到达文法的开始符号为止的过程。

三、自下而上分析的PDA

• 自左至右把输入串的符号一个一个移进栈，在移 进过程中不断查看栈顶符号串，一旦形成某个句型的 句柄时，就将此句柄用相应的产生式左部替换（归 约），若再形成句柄，就继续替换，直到栈顶不再形 成句柄为止。然后继续移进符号，重复上面的过程直 到栈顶只剩下文法的开始符号，输入串读完为止，这 样就认为识别了一个句子

优先分析法

基本思想

• 对句型中相邻的文法符号规定优先关系，以寻找句型中的句柄

• 规定句柄内各相邻符号之间具有相同的优先级

• 规定句柄两端符号优先级要比位于句柄之外而又和 句柄相邻的符号的优先级高，以先归约句柄

• 对于文法中所有符号，只要它们可能在某个句型中相邻，就要为它们规定相应的优先关系，若某两个符号 永远不可能相邻，则它们之间就无关系。

简单优先分析法

一、简单优先分析的基本思想

• PDA读入一个单词后，比较栈顶符号和该单词的优先级，若栈顶符号优先级低于该单词，继续读入；若栈顶符号优先级高于或等于读入符号，则找句柄进行归约，找不到句柄就继续读入。直到最后栈内只剩下开始符号，输入串读到“＃”为止。此时识别正确。

二、简单优先文法

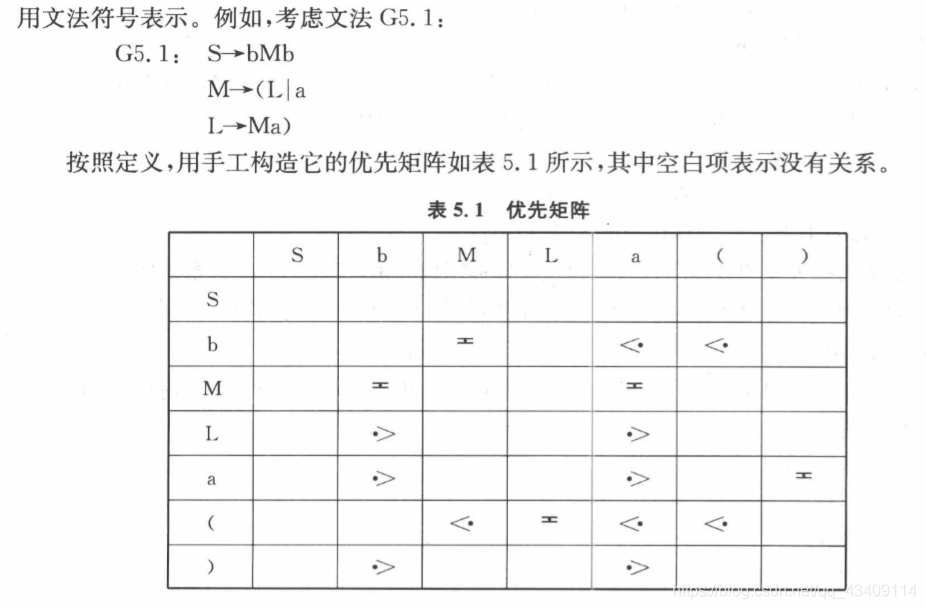
• 简单优先矩阵：根据优先关系的定义，将简单优先文法中各文法符号之间的这种关系用一个矩阵表示，称 作简单优先矩阵

• 一个文法G，如果它不含ε产生式，也不含任何右部相同的不同产生式，并且它的任何符号对(X,Y)， 或者没有关系，或者存在优先级相同或低于、高于等 关系之一，则这是一个简单优先文法
  

三、优缺点

• 技术简单、适用范围小，分析表太大

四、例子

算符优先分析法

一、基本思想

• 自下而上归约
• 规定算符(更一般地说，指终结符)的优先级及结合规则，以使得分析过程唯一
• 比较相邻两个算符而决定动作
• 这里的关键是对所有算符定义某种优先关系

二、确定运算符的优先级

• a<·b a的优先级低于b
• a=·b a的优先级等于b
• a·>b a的优先级大于b
• a和b没有任何关系

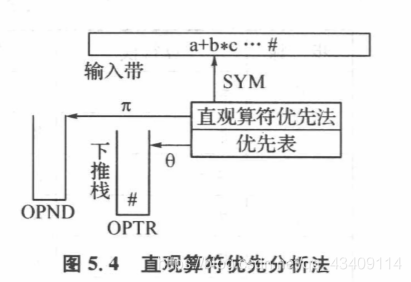
三、直观算符分析法

• 直观算符分析法使用两个工作栈：一个算符栈 （OPTR）存放运算符和括号；一个算量栈（OPND）用于存放操作数和运算结果；OPTR栈的栈顶符号用θ 表示,OPND栈的栈顶符号用π表示。伪代码如下

void Procedure():{
	Stack OPND = [];
	Stack OPTR = ['#'];
	while(true){
		Symle = scanner();
		if(OPTR.top == '#' and Symple = '#'){
			break;
		}else if(Symple is OPND){
			OPND.push(Symple);
		}else if(OPTR.top < Symple){
			OPTR.push(Symple)
		}else if(OPTR.top = Symple){
			归约();
		}else if(OPTR.top > Symple){
			归约();
		}
	}
}

四、优缺点

• 简单明了，易于手工实现，适于分析各种算 术表达式
• 算法采用两个栈，有时会把错误句子当成合 法句子；而且，它也无法指出输入串出错位置

五、算符优先文法

六、算法