Bootstrap

【读书向】阿里云天池大赛赛题解析——可视化

【读书向】阿里云天池大赛赛题解析——可视化

目录

Github 完整代码链接

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
from scipy import stats
import warnings
warnings.filterwarnings('ignore')

from sklearn.metrics import mean_squared_error

train_data = pd.read_csv('../Book/阿里云天池大赛赛题解析/input/工业蒸汽量预测/zhengqi_train.txt',sep='\t',encoding='utf-8')
test_data  = pd.read_csv('../Book/阿里云天池大赛赛题解析/input/工业蒸汽量预测/zhengqi_test.txt', sep='\t',encoding='utf-8')

train_data.head()
V0V1V2V3V4V5V6V7V8V9...V29V30V31V32V33V34V35V36V37target
00.5660.016-0.1430.4070.452-0.901-1.812-2.360-0.436-2.114...0.1360.109-0.6150.327-4.627-4.789-5.101-2.608-3.5080.175
10.9680.4370.0660.5660.194-0.893-1.566-2.3600.332-2.114...-0.1280.1240.0320.600-0.8430.1600.364-0.335-0.7300.676
21.0130.5680.2350.3700.112-0.797-1.367-2.3600.396-2.114...-0.0090.3610.277-0.116-0.8430.1600.3640.765-0.5890.633
30.7330.3680.2830.1650.599-0.679-1.200-2.0860.403-2.114...0.0150.4170.2790.603-0.843-0.0650.3640.333-0.1120.206
40.6840.6380.2600.2090.337-0.454-1.073-2.0860.314-2.114...0.1831.0780.3280.418-0.843-0.2150.364-0.280-0.0280.384

5 rows × 39 columns

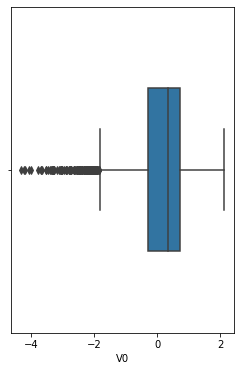
箱型图

fig = plt.figure(figsize=(4,6))
sns.boxplot(train_data['V0'],orient='v',width=0.5)

<AxesSubplot:xlabel='V0'>

在这里插入图片描述

columns = train_data.columns.tolist()[:39]
fig = plt.figure(figsize=(80,60),dpi=75)
for i in range(38):
    plt.subplot(7,8,i+1)
    sns.boxplot(train_data[columns[i]],orient='v',width=0.5)
    plt.ylabel(columns[i],fontsize=36)
plt.show()

在这里插入图片描述

获取异常数据的函数

def find_outliers(model,X,y,sigma=3):
    
    # predict y values using model
    try:
        y_pred = pd.Series(model.predict(X),index=y.index)
    # if predicting fails, try fitting the model first
    except:
        model.fit(X,y)
        y_pred = pd.Series(model.predict(X),index=y.index)
    
    # calculate residuals between the model prediction and true y values
    resid = y - y_pred
    mean_resid = resid.mean()
    std_resid  = resid.std()
    
    # calculate z statistic, define outliers to be where |z|>sigma
    z = (resid-mean_resid)/std_resid
    outliers = z[abs(z)>sigma].index
    
    # print and plot the results
    print('R2=',model.score(X,y))
    print('Mse=',mean_squared_error(y,y_pred))
    print('-------------------------------------------------------')
    
    print(len(outliers),'outliers;',' ALL data shape:',X.shape)
    
    plt.figure(figsize=(15,5))
    ax_131 = plt.subplot(1,3,1)
    plt.plot(y,y_pred,'.')
    plt.plot(y.loc[outliers],y_pred.loc[outliers],'ro')
    plt.legend(['Accepted','Outlier'])
    plt.xlabel('y')
    plt.ylabel('y_pred');
    
    ax_132 = plt.subplot(1,3,2)
    plt.plot(y,y-y_pred,'.')
    plt.plot(y.loc[outliers],y.loc[outliers]-y_pred.loc[outliers],'ro')
    plt.legend(['Accepted','Outlier'])
    plt.xlabel('y')
    plt.ylabel('y - y_pred');
    
    ax_133 = plt.subplot(1,3,3)
    z.plot.hist(bins=50,ax=ax_133)
    z.loc[outliers].plot.hist(color='r',bins=50,ax=ax_133)
    plt.legend(['Accepted','Outlier'])
    plt.xlabel('z')
    
    plt.savefig('outliers.png')
    
    return outliers

# 通过岭回归模型找出异常值，并绘制其分布
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error
X_train = train_data.iloc[:,0:-1]
y_train = train_data.iloc[:,-1]
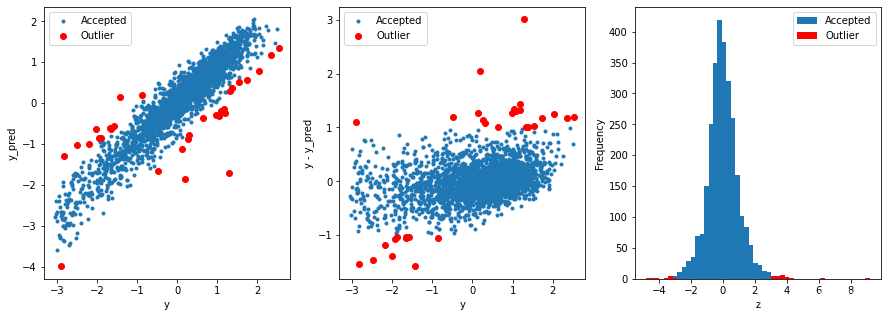
outliers = find_outliers(Ridge(),X_train,y_train)

R2= 0.8890858938210388
Mse= 0.10734857773123628
-------------------------------------------------------
31 outliers;  ALL data shape: (2888, 38)

在这里插入图片描述

直方图和Q-Q图

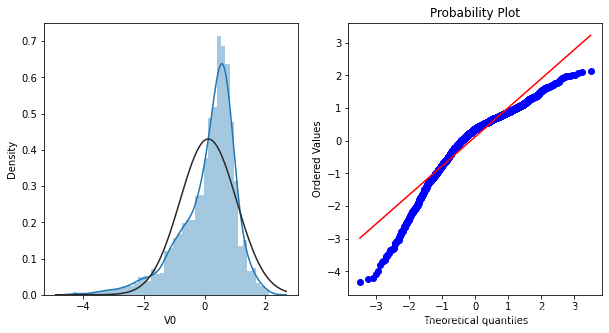
Q-Q图是指数据的分位数和正态分布的分位数对比参照的图，如果数据符合正态分布，则所有的点都会落在直线上。首先，通过绘制变量V0的直方图查看其在训练集集中的统计分布，并绘制Q-Q图查看V0的分布是否近似于正态分布

plt.figure(figsize=(10,5))

ax = plt.subplot(1,2,1)
sns.distplot(train_data['V0'],fit=stats.norm)
ax = plt.subplot(1,2,2)
res = stats.probplot(train_data['V0'],plot=plt)

在这里插入图片描述

train_cols = 6
train_rows = len(train_data.columns)
plt.figure(figsize=(4*train_cols,4*train_rows))

i = 0
for col in train_data.columns:
    i+=1
    ax = plt.subplot(train_rows,train_cols,i)
    sns.distplot(train_data[col],fit=stats.norm)

    i+=1
    ax = plt.subplot(train_rows,train_cols,i)
    stats.probplot(train_data[col],plot=plt)

# tight_layout会自动调整子图参数，使之填充整个图像区域
plt.tight_layout()
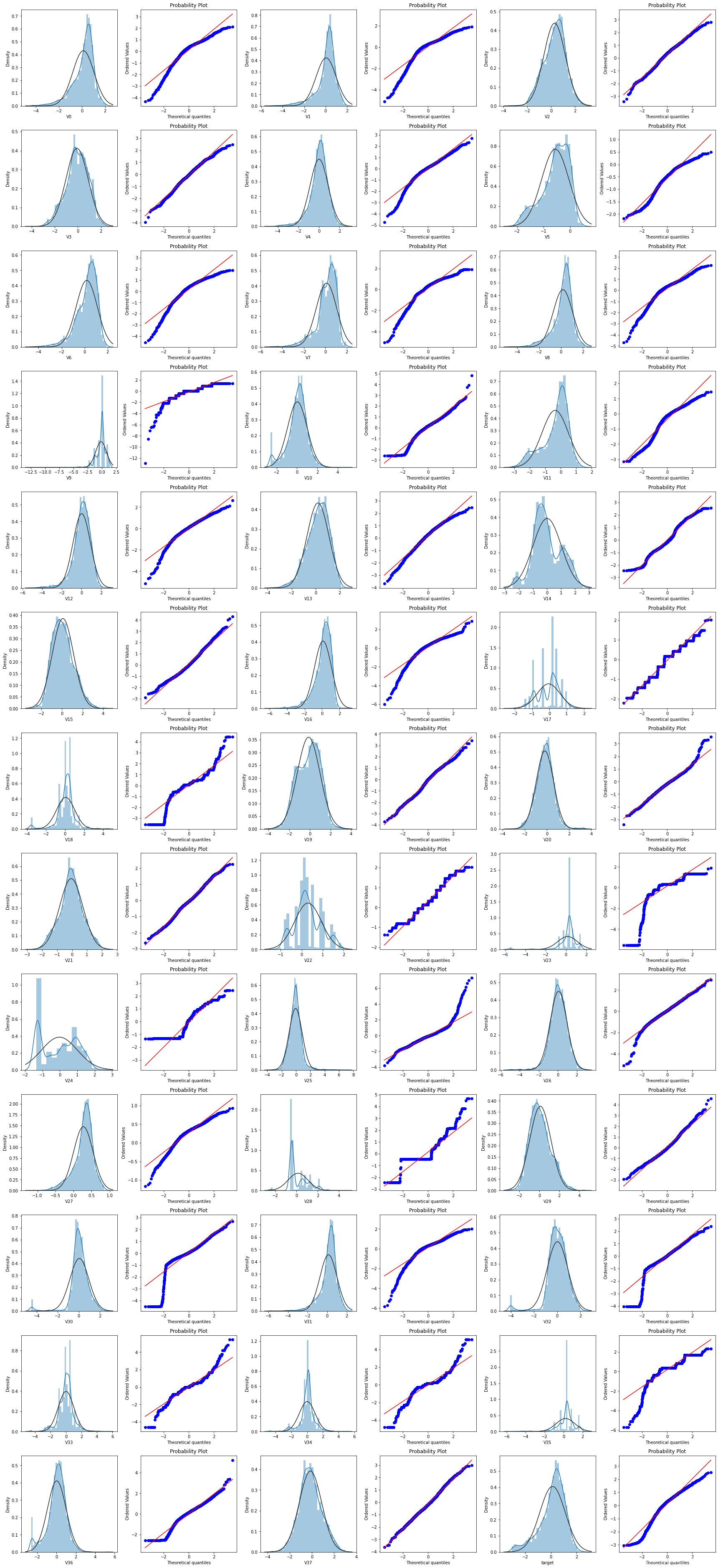
plt.show()

在这里插入图片描述

很多特征变量如V1,V9,V24,V28等的数据分布不是正态的，数据并不跟随对角线分布，后续可以使用数据变换对其进行处理

KDE分布图

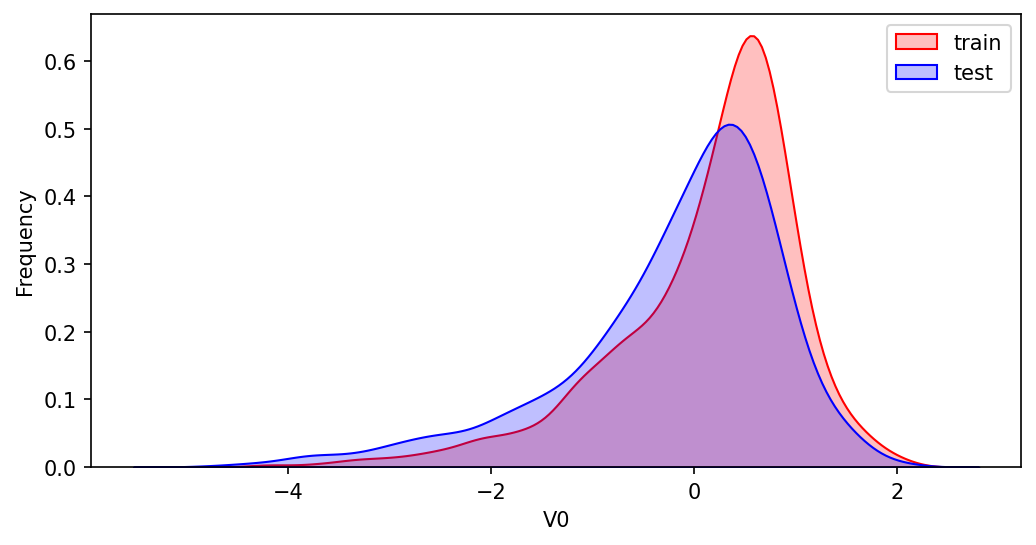
KDE核密度估计 可以理解为是对直方图的加窗平滑。通过绘制KDE分布图，可以查看并对比训练集和测试集中特征变量的分布情况，发现两个数据集中分布不一致的特征变量。

col_name = 'V0'
plt.figure(figsize=(8,4),dpi=150)
ax = sns.kdeplot(train_data[col_name],color='Red',shade=True)
ax = sns.kdeplot(test_data[col_name],color='Blue',shade=True)
ax.set_xlabel(col_name)
ax.set_ylabel('Frequency')
ax = ax.legend(['train','test'])

在这里插入图片描述

dist_cols = 6
dist_rows = len(test_data.columns)
plt.figure(figsize=(4*dist_cols,4*dist_rows))
i = 1
for col in test_data.columns:
    ax = plt.subplot(dist_rows,dist_cols,i)
    ax = sns.kdeplot(train_data[col],color='Red',shade=True)
    ax = sns.kdeplot(test_data[col],color='Blue',shade=True)
    ax.set_xlabel(col)
    ax.set_ylabel('Frequency')
    ax = ax.legend(['train','test'])
    i+=1
plt.show()

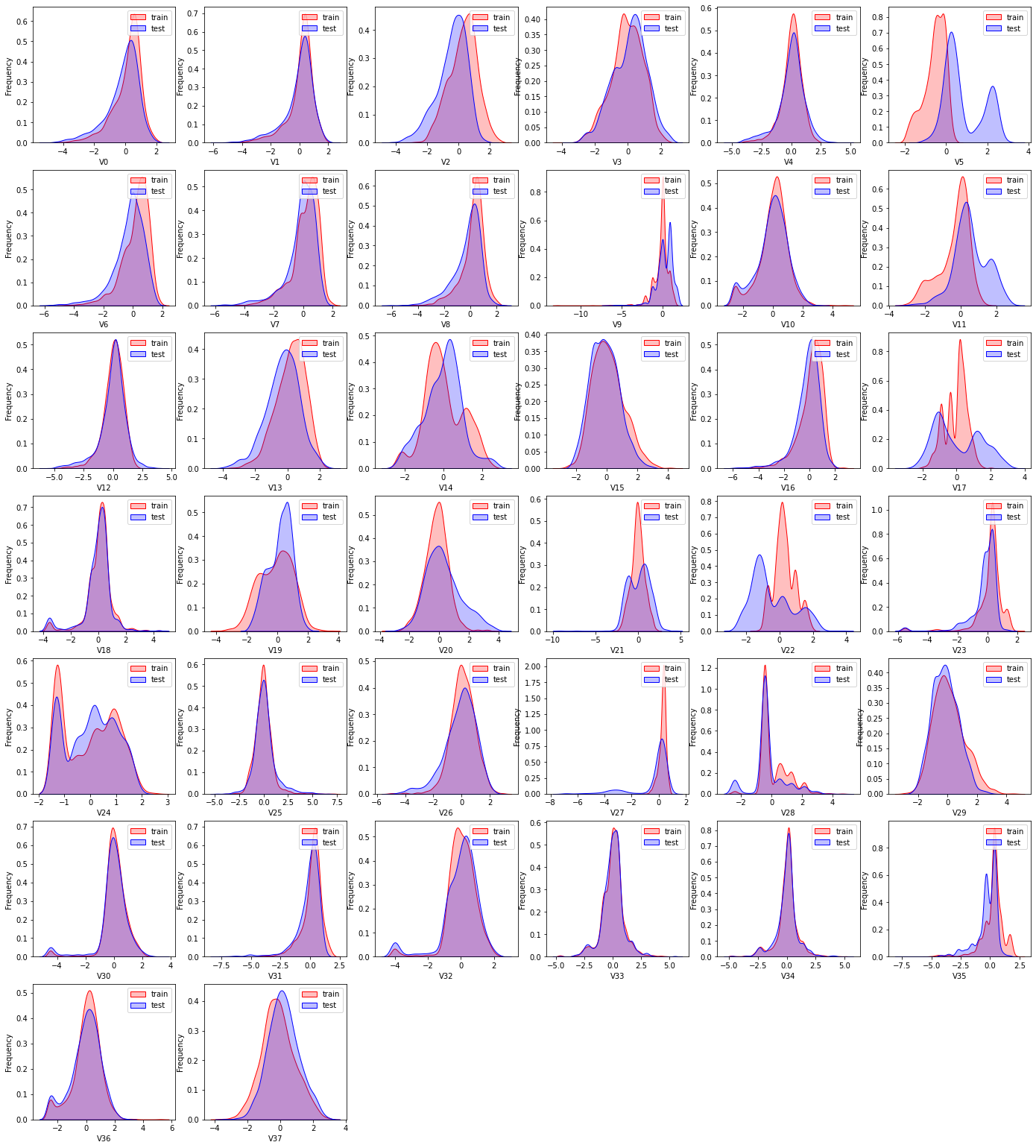
在这里插入图片描述

可以发现，特征变量V5 V9 V11 V17 V22 V28在训练集和测试集中的分布不一致，这会导致模型的泛化能力变差，需要删除此类特征

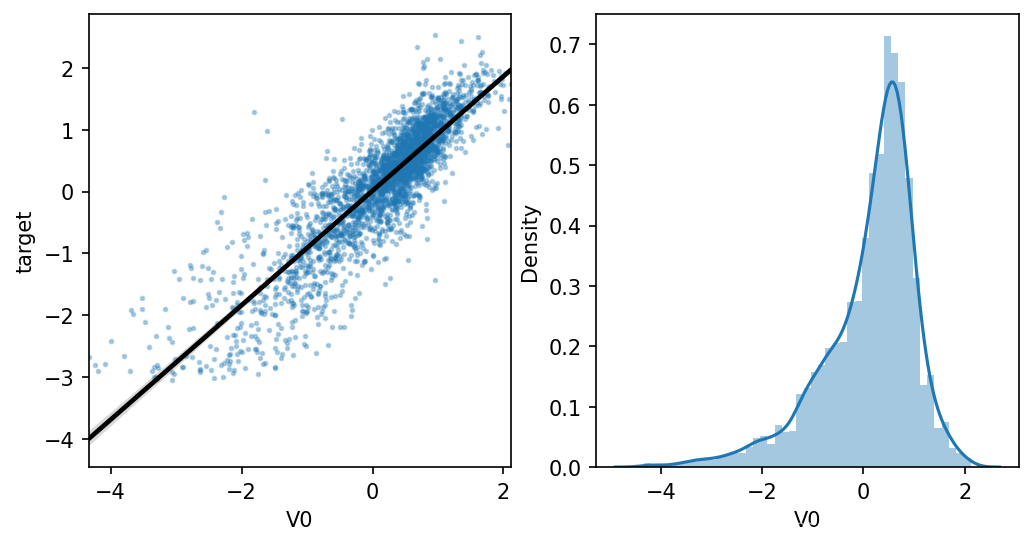
线性回归图

fcols = 2
frows = 1
plt.figure(figsize=(8,4),dpi=150)

ax = plt.subplot(1,2,1)
sns.regplot(x='V0',y='target',data=train_data,ax=ax,
           scatter_kws={'marker':'.','s':3,'alpha':0.3},
           line_kws={'color':'k'});
plt.xlabel('V0')
plt.ylabel('target')

ax = plt.subplot(1,2,2)
sns.distplot(train_data['V0'].dropna())
plt.xlabel('V0')

plt.show()

在这里插入图片描述

fcols = 6
frows = len(test_data.columns)
plt.figure(figsize=(5*fcols,4*frows))

i = 0
for col in test_data.columns:
    i+=1
    ax=plt.subplot(frows,fcols,i)
    sns.regplot(x=col,y='target',data=train_data,ax=ax,
               scatter_kws={'marker':'.','s':3,'alpha':0.3},
               line_kws={'color':'k'});
    plt.xlabel(col)
    plt.ylabel('target')
    
    i+=1
    ax = plt.subplot(frows,fcols,i)
    
    sns.distplot(train_data[col].dropna())
    plt.xlabel(col)
    
plt.tight_layout()
plt.show()

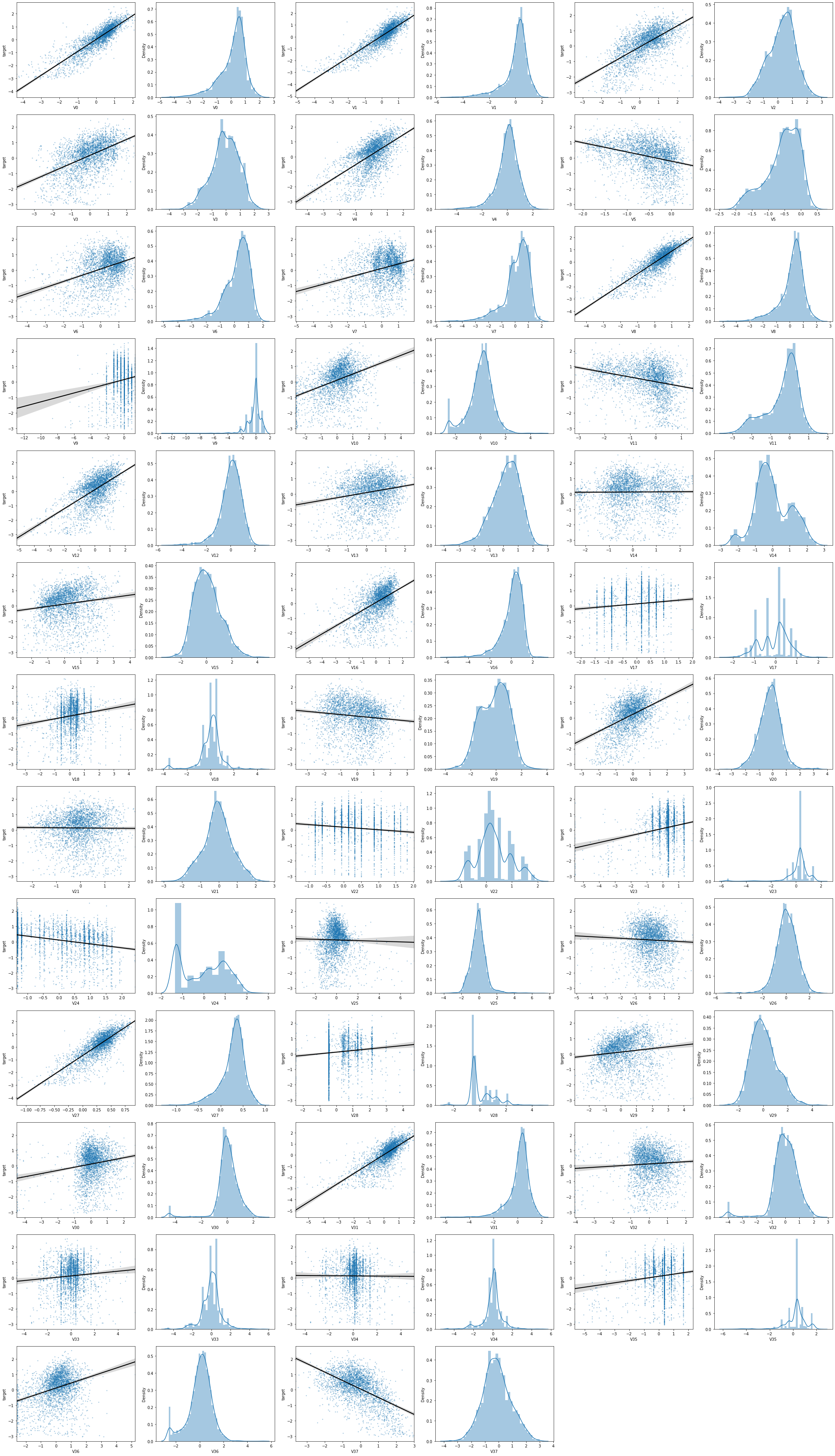
在这里插入图片描述

查看所有特征变量与Target变量的线性回归关系

特征变量的相关性

pd.set_option('display.max_columns',10)
pd.set_option('display.max_rows',10)
data_train1 = train_data.drop(['V5', 'V9', 'V11', 'V17', 'V22', 'V28'],axis=1)
train_corr = data_train1.corr()

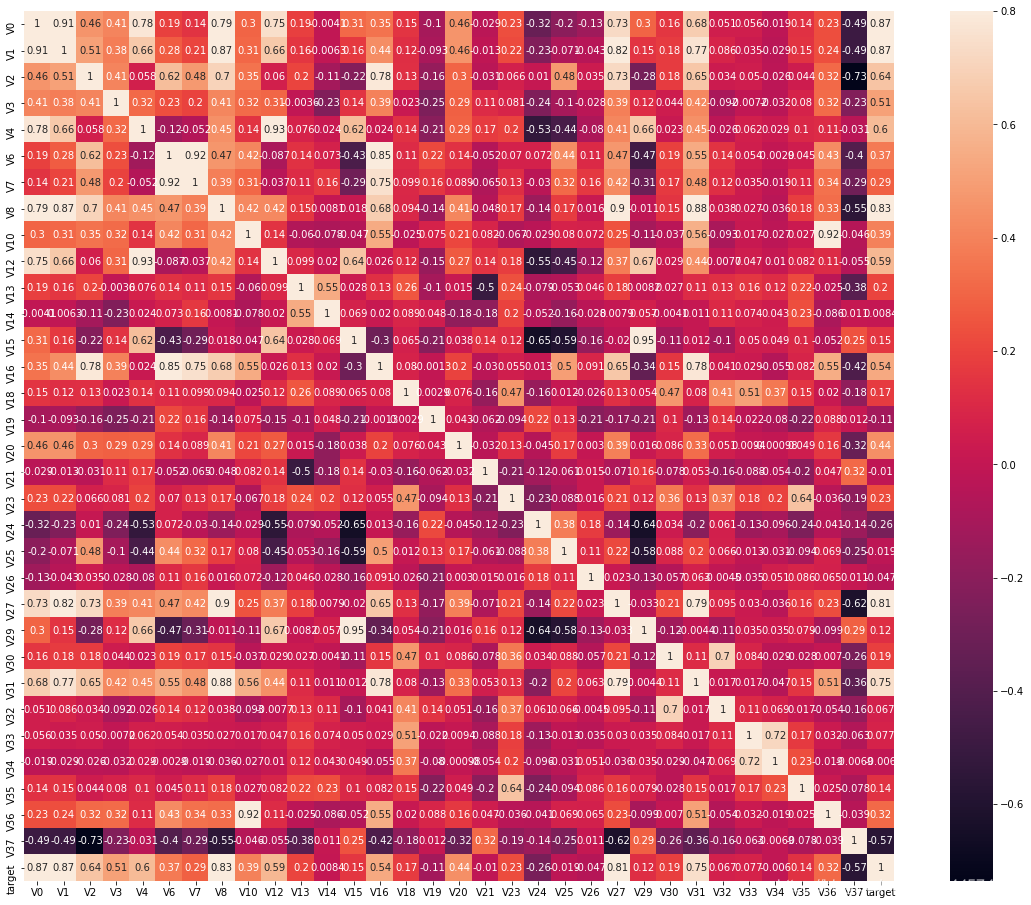
ax = plt.subplots(figsize=(20,16))
ax = sns.heatmap(train_corr,vmax=.8,square=True,annot=True)

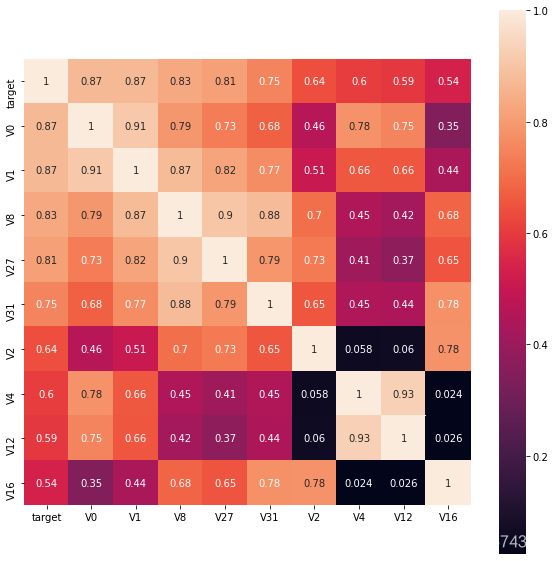
在这里插入图片描述

寻找K个与target变量最相关的特征变量

k = 10
cols = train_corr.nlargest(k,'target')['target'].index

cm = np.corrcoef(train_data[cols].values.T)
hm = plt.subplots(figsize=(10,10))
hm = sns.heatmap(train_data[cols].corr(),annot=True,square=True)
plt.show()

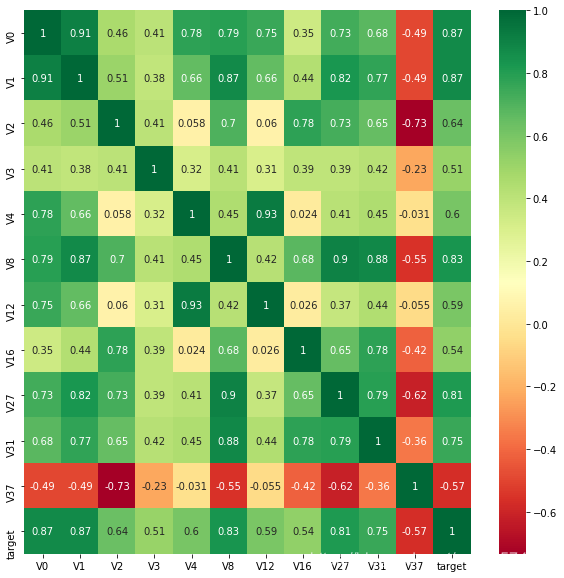
在这里插入图片描述

找出与target变量的相关系数大于0.5的特征变量

threshold = 0.5

corrmat = train_data.corr()
top_corr_features = corrmat.index[abs(corrmat['target'])>threshold]
plt.figure(figsize=(10,10))
g = sns.heatmap(train_data[top_corr_features].corr(),annot=True,cmap='RdYlGn')

在这里插入图片描述

说明：相关性选择主要用于判别线性相关，对于target变量如果存在更复杂的函数形式影响，则建议使用树模型的特征重要性去选择

# 用相关系数阈值移除相关特征
threshold = 0.5

corr_matrix = data_train1.corr().abs()
drop_col = corr_matrix[corr_matrix['target']<threshold].index
# data_all.drop(drop_col,axis=1,inplace=True)

Box-Cox变换

在连续的响应变量不满足正态分布时，可以使用Box-Cox变换，可使线性回归模型在满足线性、正态性、独立性及方差齐性的同时，又不丢失信息。

在Box-Cox变换后，可以在一定程度上减小不可观测的误差和预测变量的相关性，这有利于线性模型的拟合及分析出特征的相关性。

在Box-Cox变换之前，需要对数据做归一化预处理

drop_columns = ['V5', 'V9', 'V11', 'V17', 'V22', 'V28']
# 合并训练集和测试集
train_x = train_data.drop(['target'],axis=1)
train_x['flag'] = 'train'
test_data['flag'] = 'test'

data_all = pd.concat([train_x,test_data],axis=0,ignore_index=True)
data_all.drop(drop_columns,axis=1,inplace=True)

# 归一化
cols_numeric = [i for i in list(data_all.columns) if i!='flag']

def scale_minmax(col):
    return (col-col.min())/(col.max()-col.min())

data_all[cols_numeric] = data_all[cols_numeric].apply(scale_minmax,axis=0)

train_data_process = data_all[data_all['flag']=='train']
train_data_process.drop(['flag'],axis=1,inplace=True)

cols_numeric_left = cols_numeric[:13]
cols_numeric_right = cols_numeric[13:]
train_data_process = pd.concat([train_data_process,train_data['target']],axis=1)

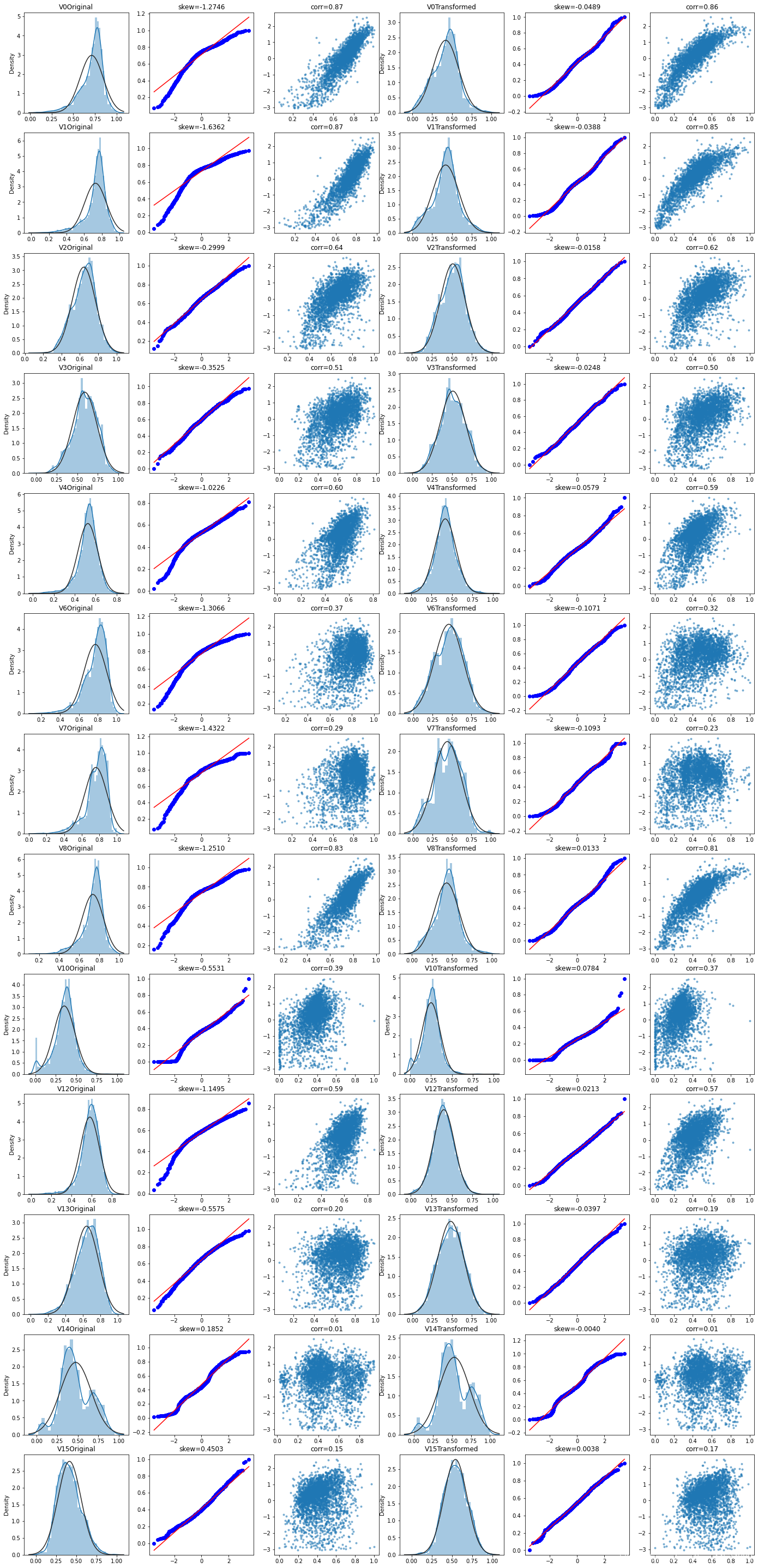
fcols = 6
frows = len(cols_numeric_left)
plt.figure(figsize=(4*fcols,4*frows))
i=0

for var in cols_numeric_left:
    dat = train_data_process[[var,'target']].dropna()
    i+=1
    plt.subplot(frows,fcols,i)
    sns.distplot(dat[var],fit=stats.norm)
    plt.title(var+' Original')
    plt.xlabel('')
    i+=1
    plt.subplot(frows,fcols,i)
    _ = stats.probplot(dat[var],plot=plt)
    plt.title('skew='+'{:.4f}'.format(stats.skew(dat[var])))
    plt.xlabel('')
    plt.ylabel('')
    i+=1
    plt.subplot(frows,fcols,i)
    plt.plot(dat[var],dat['target'],'.',alpha=0.5)
    plt.title('corr=' + '{:.2f}'.format(np.corrcoef(dat[var],dat['target'])[0][1]))
    
    i+=1
    plt.subplot(frows,fcols,i)
    trans_var,lambda_var = stats.boxcox(dat[var].dropna()+1)
    trans_var = scale_minmax(trans_var)
    sns.distplot(trans_var,fit=stats.norm)
    plt.title(var + ' Transformed')
    plt.xlabel('')
    i+=1
    plt.subplot(frows,fcols,i)
    _ = stats.probplot(trans_var,plot=plt)
    plt.title('skew='+'{:.4f}'.format(stats.skew(trans_var)))
    plt.xlabel('')
    plt.ylabel('')
    i+=1
    plt.subplot(frows,fcols,i)
    plt.plot(trans_var,dat['target'],'.',alpha=0.5)
    plt.title('corr='+'{:.2f}'.format(np.corrcoef(trans_var,dat['target'])[0][1]))

在这里插入图片描述

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
目标检测中的数据增强，包括bbox的变换
树莓派和主机相互PING
二、Numpy库
结构方程模型amos的操作与应用pdf_AMOS结构方程进行医学问卷量表分析教程（一阶简单路径效应分析）...
java big5_BIG5编码表
ubantu安装qemu虚拟机
Java中使用volatile关键字内部调用接口的实现方法
一篇学会Gitlab搭建及使用
java系列2：java测试框架Junit5+Allure+Mockito
STM32 硬件I2C外设
;