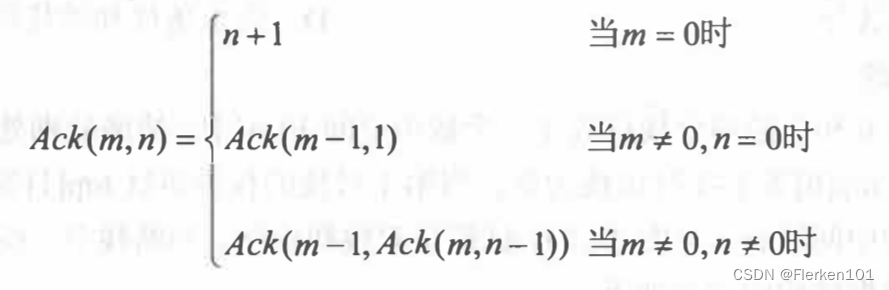习题一
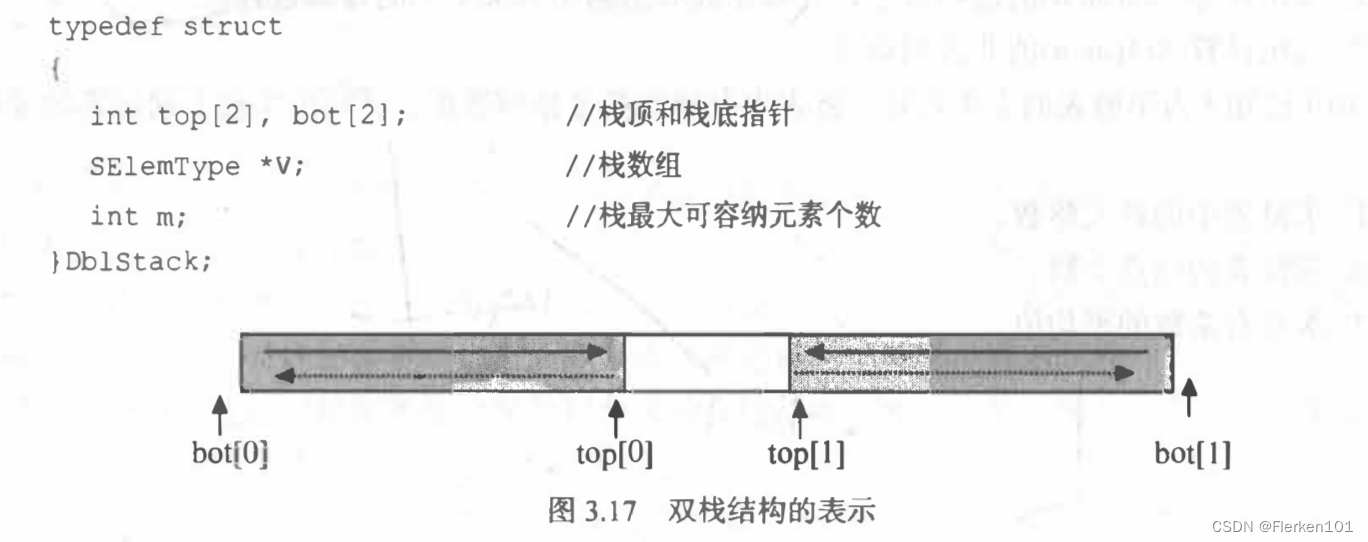
将编号为 0 和 1 的两个栈存放于一个数组空间 V[m]中,栈底分别处于数组的两端。当第0 号栈的栈顶指针 top[0]等于-1 时该栈为空;当第 1 号栈的栈顶指针 top[1]等于 m 时,该栈为空。两个栈均从两端向中间增长(见下图)。试编写双栈初始化,判断栈空、栈满、进栈和出栈等算法的函数。双栈数据结构的定义如下;
#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 7
typedef char SElemType;
typedef struct {
int top[2];
int bot[2];
SElemType* v;
int m;
}DblStack;
void InitDblStack(DblStack& S);
int EmptyDblStack(DblStack& S);
int FullDblStack(DblStack& S);
void PushLeft(DblStack& S, SElemType e);
void PushRight(DblStack& S, SElemType e);
SElemType PopLeft(DblStack& S);
SElemType PopRight(DblStack& S);
void printDblStack(DblStack& S);
int main()
{
DblStack N = { {0,0},{0,0},NULL,0 };
InitDblStack(N);
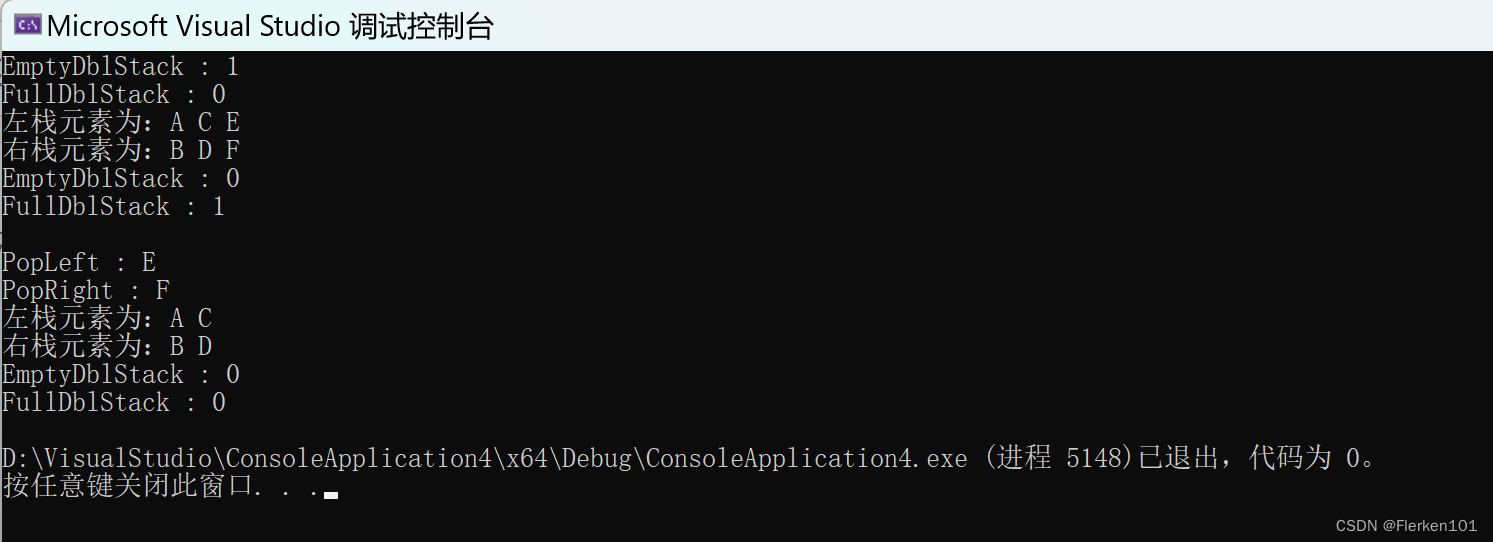
printf("EmptyDblStack : %d\n", EmptyDblStack(N));
printf("FullDblStack : %d\n", FullDblStack(N));
PushLeft(N, 'A');
PushRight(N, 'B');
PushLeft(N, 'C');
PushRight(N, 'D');
PushLeft(N, 'E');
PushRight(N, 'F');
printDblStack(N);
printf("\nEmptyDblStack : %d\n", EmptyDblStack(N));
printf("FullDblStack : %d\n", FullDblStack(N));
printf("\nPopLeft : %c\n", PopLeft(N));
printf("PopRight : %c\n", PopRight(N));
printDblStack(N);
printf("\nEmptyDblStack : %d\n", EmptyDblStack(N));
printf("FullDblStack : %d\n", FullDblStack(N));
return 0;
}
void InitDblStack(DblStack& S)
{
S.v = (SElemType*)malloc(sizeof(SElemType) * MAXSIZE);
S.m = MAXSIZE;
S.bot[0] = -1;
S.top[0] = -1;
/*选择 - 1 作为空栈的初始值是一种较为常见的实践, - 1作为一个无效索引,
无需担心栈顶指针(栈顶所在位置的下标)与数组下标的边界冲突问题,清晰地标记了栈的初始空状态。*/
S.bot[1] = S.m-1;
S.top[1] = S.m-1;
/* 考虑到数组下标习惯,在双端栈中,会把右栈的栈底也设在数组的末尾位置,即索引m - 1,
表示如果有元素入栈,它将从这个位置开始。
同时,右栈的栈顶也初始化为m-1,表明此时右栈为空。*/
}
int EmptyDblStack(DblStack &S)
{
//空返回1
if ((S.top[0] == -1) && (S.top[1] == S.m-1))
{
return 1;
}
else
{
return 0;
}
}
int FullDblStack(DblStack& S)
{
if (S.top[1] == S.top[0] || S.top[0] >= S.m-1 || S.top[1] < 0)
//三种满栈情况左右两栈中间相遇,左栈满,右栈满
return 1;//满栈返回1
return 0;//否则返回0
}
/*
//第二种满栈的判断方式:栈中的元素个数等于数组v的长度
int FullDblStack(DblStack& S)
{
//满返回1
if (S.top[0] -1- S.bot[0] + S.bot[1] - (S.top[1]-1) >= S.m)
{
return 1;
}
else
{
return 0;
}
}
*/
//若0号栈(左栈)不满,则进入0号栈,否则进入1号栈(右栈)
//左栈进栈
void PushLeft(DblStack& S, SElemType e)
{
if (FullDblStack(S) == 1)
{
printf("栈已满不能进行进栈操作。\n");
return;
}
if (S.top[0] == -1) //S.bot[0] 初始化之后始终为-1
{
S.top[0] = S.top[0] + 1;
S.v[S.top[0]] = e;
S.top[0] = S.top[0] + 1;
}
else
{
S.v[S.top[0]] = e;
S.top[0] = S.top[0] + 1;
}
}
//右栈进栈
void PushRight(DblStack& S, SElemType e)
{
if (FullDblStack(S) == 1)
{
printf("栈已满不能进行进栈操作。\n");
return;
}
//S.bot[1] 初始化之后始终为 m-1
S.v[S.top[1]] = e;
S.top[1] = S.top[1] - 1;
}
//左栈出栈
SElemType PopLeft(DblStack& S)
{
if (S.top[0] == -1)
{
printf("左栈已空,无法进行出栈操作\n");
return '\0';
}
SElemType e = S.v[S.top[0]-1];
S.top[0] = S.top[0]-1;
return e;
}
//右栈出栈
SElemType PopRight(DblStack& S)
{
if (S.top[1] == S.m - 1)
{
printf("右栈已空,无法进行出栈操作\n");
return '\0';
}
SElemType e = S.v[S.top[1]+1];
S.top[1] = S.top[1] + 1;
return e;
}
//遍历双栈
void printDblStack(DblStack& S)
{
int i = 0;
int j = 0;
printf("左栈元素为:");
for (i = 0; i < S.top[0]; i++)
{
SElemType a = S.v[i];
printf("%c ", a);
}
printf("\n右栈元素为:");
for (j = 0; j < S.bot[1]-S.top[1]; j++)
{
SElemType b = S.v[S.bot[1]-j];
printf("%c ", b);
}
}
习题二
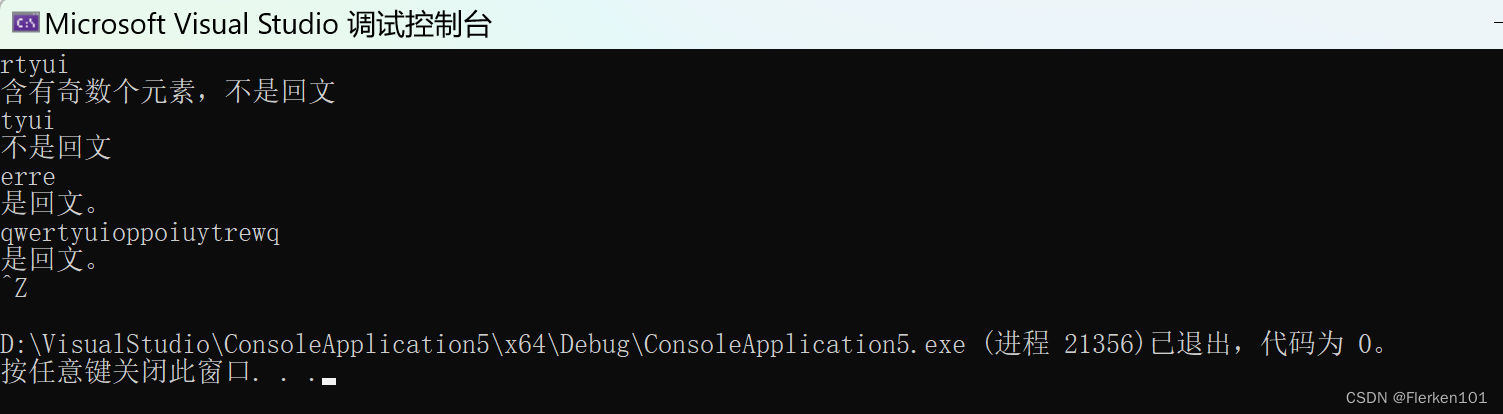
回文是指正读反读均相同的字符序列,如 “abba” 和 “abdba” 均是回文,但 “good” 不是回文。试写一个算法判定给定的字符序列是否为回文。(提示:将一半字符入栈)
不要在main函数的中间部分随意加入return 0;
main函数的return 0;代表的是结束整个程序。
break是指结束整个while/for循环,执行循环外后面的语句;
continue是指结束本次循环,
在while循环中是执行下一次循环的判定。
在for循环中,便是执行for中的循环变量增值,即语句3.
[ 但for循环的执行过程是:1-2-4-3—2-4-3—2-4-3—2-4-3……
除第一次循环,语句2是每次循环的开始。]
//使用链栈
#include <stdio.h>
#include <stdlib.h>
typedef struct StackNode
{
char data;
struct StackNode* next;
}StackNode, * LinkStack;
#define MAXSIZE 100
int getword(char* s, int LIMIT);
void InitStack(LinkStack& S);
void Push(LinkStack& S, char e);
char Pop(LinkStack& S);
void compare(LinkStack& S, char* s, int LEN);
int main()
{
char v[MAXSIZE];
int len = 0;
int i = 0;
LinkStack N = NULL;
//连续判断,字符串长度不为0
while ((len = getword(v, MAXSIZE)) > 0)
{
//长度为奇数,一定不是回文
if (len % 2)
{
printf("含有奇数个元素,不是回文\n");
}
else
{
InitStack(N);
for (i = 0; i < len / 2; i++)
{
Push(N, v[i]);
}
compare(N, v, len);
}
}
return 0;
}
//取输入的字符串,返回长度
int getword(char* s,int LIMIT)
{
int i = 0;
int c = 0;
for (i = 0; (i < LIMIT -1) && ((c = getchar()) != EOF) && (c != '\n'); i++)
{
s[i] = c;
}
return i;
}
//初始化栈
void InitStack(LinkStack& S)
{
S = NULL;
}
//入栈
void Push(LinkStack& S, char e)
{
struct StackNode* p = NULL;
p = (struct StackNode*)malloc(sizeof(struct StackNode));
p->data = e;
p->next = S;
S = p;
}
//出栈
char Pop(LinkStack& S)
{
struct StackNode* p = S;
char r = '\0';
if (S)
{
p = S;
S = S->next;
r = p->data;
free(p);
}
return r;
}
//将出栈元素依次与输入字符串中的下一个字符进行比较
void compare(LinkStack& S, char* s, int LEN)
{
char a = '\0';
char b = '\0';
int i = 0;
for (i = LEN / 2; i < LEN && S; i++)
{
b = s[i];
a = Pop(S);
if (a != b)
{
printf("不是回文\n");
return;
}
}
printf("是回文。\n");
}
习题三
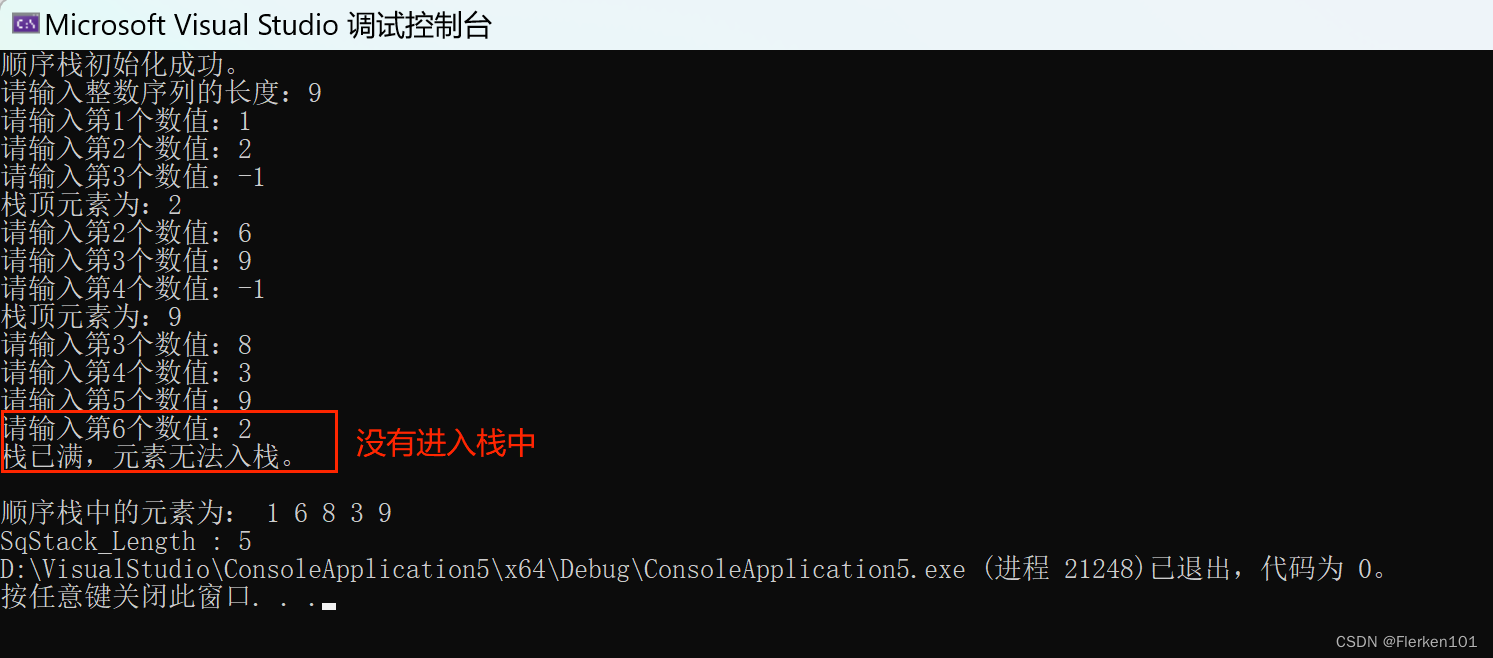
设从键盘输入一整数的序列:a1, a2, a3, … ,a(n) , 试编写算法实现:用栈结构存储输入的整数,当 a(i) ≠ -1 时,将 a(i)进栈;当 a(i) = -1 时,输出栈顶整数并出栈。算法应对异常情况(入栈满等) 给出相应的信息。
//使用顺序栈
#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 5
typedef struct
{
int* base;
int* top;
int stacksize;
}SqStack;
void InitStack(SqStack& S);
void Push(SqStack& S, int e);
int Pop(SqStack& S);
void printfSqStack(SqStack& S);
int main()
{
SqStack N = { NULL,NULL,0};
int len = 0;
int num = 0;
int i = 0;
int a = 0;
InitStack(N);
printf("请输入整数序列的长度:");
scanf_s("%d", &len);
for (i = 0; i < len; i++)
{
printf("请输入第%d个数值:",i+1);
scanf_s(" %d", &num);
if (num != -1)
{
if (N.top - N.base == N.stacksize)
{
printf("栈已满,元素无法入栈。\n");
break;
}
else
{
Push(N, num);
}
}
else
{
a = Pop(N);
printf("栈顶元素为:%d\n", a);
i = i-2;
}
}
printfSqStack(N);
return 0;
}
//初始化
void InitStack(SqStack &S)
{
S.base = (int*)malloc(sizeof(int) * MAXSIZE);
S.top = S.base;
S.stacksize = MAXSIZE;
printf("顺序栈初始化成功。\n");
}
//入栈
void Push(SqStack& S,int e)
{
if (S.top - S.base >= MAXSIZE)
{
printf("栈已满,元素无法入栈。\n");
return;
}
*S.top = e;
S.top++;
}
//出栈
int Pop(SqStack& S)
{
if (S.top == S.base)
{
printf("栈为空,元素无法出栈。\n");
}
int e = *(S.top - 1);
S.top--;
return e;
}
void printfSqStack(SqStack& S)
{
int i = 0;
int e = 0;
printf("\n顺序栈中的元素为:");
for (i = 0; i < (S.top - S.base); i++)
{
e = S.base[i];
printf(" %d", e);
}
printf("\nSqStack_Length : %d", i);
}
习题四
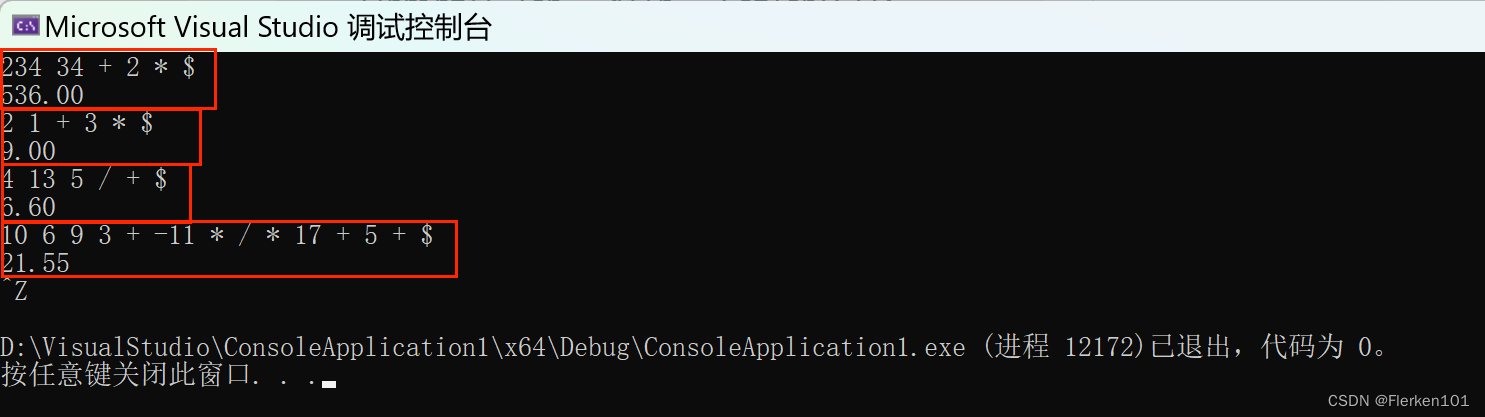
从键盘上输入一个后缀表达式,试编写算法计算表达式的值。规定:逆波兰表达式的长度不超过一行,以 " $ "作为输入结束,操作数之间用空格分隔,操作符只可能有+、—、*、/四种 运算。例如:234 34 + 2 * $。
4.3外部变量:逆波兰表达式——C语言实现计算器 ——Flerken101
#include <stdio.h>
#include <stdlib.h>
#include <ctype.h>
#define OK 1
#define ERROR 0
#define OVERFLOW -2
#define MAXSIZE 100
typedef int Status;
typedef double SElemType;
typedef struct {
SElemType* base;
SElemType* top;
int stacksize;
}SqStack;
void InitStack(SqStack&S);
void Push(SqStack& S, SElemType e);
SElemType Pop(SqStack& S);
SElemType GetTop(SqStack& S);
int getline(char array[], int limit);
double atof(char s[]);
double Postfix(char* t);
int main() {
double x;
char t[100];
int len = 0;
while ((len = getline(t, MAXSIZE)) > 0)
{
x = Postfix(t);
printf("%.2f\n", x);
}
return 0;
}
void InitStack(SqStack& S)
{
S.base = (SElemType*)malloc(MAXSIZE * sizeof(SElemType));
if (!S.base)
printf("内存分配失败,初始化失败\n");
S.top = S.base;
S.stacksize = MAXSIZE;
}
void Push(SqStack& S, SElemType e)
{
if (S.top - S.base == S.stacksize)
printf("顺序栈已满,元素无法入栈。\n");
*(S.top++) = e;
}
SElemType Pop(SqStack& S)
{
if (S.base == S.top)
printf("顺序栈为空,元素无法出栈。\n");
SElemType e = *(--S.top);
return e;
}
SElemType GetTop(SqStack& S)
{
if (S.top != S.base)
return *(S.top - 1);
else
return -1;
}
//取输入的字符串,返回长度
int getline(char array[], int limit)
{
int i, c;
i = c = 0;
for (i = 0; i < limit - 1 && (c = getchar()) != EOF && c != '\n'; i++)
{
array[i] = c;
}
if (c == '\n')
{
array[i++] = c;
}
array[i] = '\0';
return i;
}
double atof(char s[])
{
double val, power;
int i, sign;
for (i = 0; isspace(s[i]); i++)
{
;
}
sign = (s[i] == '-') ? -1 : 1;
if (s[i] == '+' || s[i] == '-')
{
i++;
}
for (val = 0.0; s[i] >= '0' && s[i] <= '9'; i++)
{
val = 10.0 * val + (s[i] - '0');
}
if (s[i] == '.')
{
i++;
}
for (power = 1.0; s[i] >= '0' && s[i] <= '9'; i++)
{
val = 10.0 * val + (s[i] - '0');
power *= 10.0;
}
return sign * val / power;
}
double Postfix(char* t)
{
SqStack S;
InitStack(S);
SElemType x = 0;
int i = 0;
int j = 0;
int k = 0;
int n = 0;
char r[MAXSIZE];
while (t[i] != '$')
{
if ((t[i] >= '0' && t[i] <= '9') || t[i] == '.' || ((t[i] == '+' || t[i] == '-') && ((t[i + 1] >= '0' && t[i + 1] <= '9') || t[i + 1] == '.')))
{
//printf("***************第一个if***************\n");
if ((t[i - 2] == '+' || t[i - 2] == '-' || t[i - 2] == '*' || t[i - 2] == '/') && t[i - 1] == ' ')
{
//printf("***************第二个if***************\n");
for (j = 0; j<=k; j++)
r[j] = 0;
j = 0;
}
if ((t[i] == '+' || t[i] == '-') && ((t[i + 1] >= '0' && t[i + 1] <= '9') || t[i + 1] == '.'))
{
//printf("***************第三个if***************\n");
r[j] = t[i];
j++;
i++;
}
r[j] = t[i];
//printf("t[%d] = %c\n", i, t[i]);
//printf("r[%d] = %c\n", j, r[i]);
j++;
i++;
if (k+1 > j)
{
//printf("***************第四个if***************\n");
for (n = j+1; k >= n;n++)
r[n] = 0;
}
x = atof(r);
//printf("x = %f\n", x);
k = j;
if (t[i] == ' ')
{
//printf("***************第五个if***************\n");
Push(S, x);
j = 0;
}
//printf("t[%d] = %c\n", i+1, t[i+1]);
//printf("t[%d] = %c\n", i +2, t[i + 2]);
if ((t[i] == ' ') && ((t[i + 1] >= '0' && t[i + 1] <= '9') || t[i + 1] == '.' || ((t[i + 1] == '+' || t[i + 1] == '-') && ((t[i + 2] >= '0' && t[i + 2] <= '9') || t[i + 2] == '.'))))
{
//printf("***************第六个if***************\n");
for (j = 0; j <= k; j++)
r[j] = 0;
j = 0;
}
}
else if (t[i] == ' ')
{
i++;
}
else
{
SElemType a = 0;
SElemType b = 0;
SElemType c = 0;
a = Pop(S);
//printf("a = %f\n", a);
b = Pop(S);
//printf("b = %f\n", b);
//printf("t[%d] = %c\n", i, t[i]);
switch (t[i])
{
case '+':
c = b + a;
break;
case '-':
c = b - a;
break;
case '*':
c = b * a;
break;
case '/':
c = b / a;
break;
default:
break;
}
//printf("c = %f\n", c);
Push(S, c);
i++;
}
}
//printf("Top = %f\n", GetTop(S));
return GetTop(S);
}
习题五
假设以 I 和 O 分别表示入栈和出栈操作。栈的初态和终态均为空,入栈和出栈的操作序 列可表示为仅由 I 和 O 组成的序列,称可以操作的序列为合法序列,否则称为非法序列。
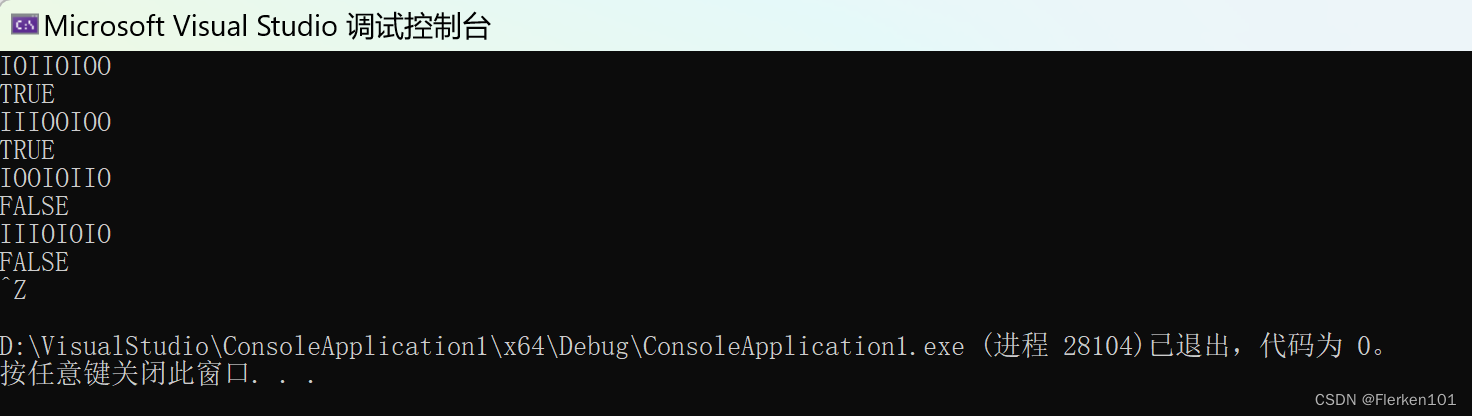
① 下面所示的序列中哪些是合法的?
A. IOIIOIOO B. IOOIOIIO C. IIIOIOIO D. IIIOOIOO
A和D是合法的。
B由于只进栈一个元素,而要出栈两个元素,不合法;
C由于最终栈不为空,所以不合法。
② 通过对①的分析,写出一个算法,判定所给的操作序列是否合法。若合法,返回 true, 否则返回 false (假定被判定的操作序列已存入一维数组中)。
人为判断:相邻的 I 和相邻的 O 是分别是一个整体,I和O仅是一个符号;
按顺序,依次数I和O的个数,静态序列;
计算机判断:
每一个I和O都是不同的单独整体,表示一种动作。
利用栈的特性,按给出的序列顺序,进入动作I 和 退出动作O 不断发生的动态过程,栈中的元素在不断发生变化。
栈练习之Example006-判定给定的由 I 和 O 组成的入栈和出栈组成的操作序列是否合法——二木成林
//利用顺序栈:I则压入栈中,O则将一个I出栈
#include <stdio.h>
#include <stdlib.h>
#define MAXSIZE 100
typedef struct
{
char* base;
char* top;
int stacksize;
}SqStack;
void InitStack(SqStack& S);
void Push(SqStack& S, char e);
char Pop(SqStack& S);
int EmptyStack(SqStack& S);
int getword(char* s, int limit);
void Judgelegality(char* s);
int main()
{
char t[MAXSIZE];
int length = 0;
while((length = getword(t, MAXSIZE)) > 0)
{
Judgelegality(t);
}
return 0;
}
void InitStack(SqStack& S)
{
S.base = (char*)malloc(sizeof(char) * MAXSIZE);
if (!S.base)
{
printf("内存分配失败,初始化失败。\n");
return;
}
S.top = S.base;
S.stacksize = MAXSIZE;
}
void Push(SqStack& S,char e)
{
if (S.top - S.base == S.stacksize)
{
printf("栈已满,元素无法入栈。\n");
return;
}
*(S.top) = e;
S.top++;
}
char Pop(SqStack& S)
{
if (S.base == S.top)
{
printf("栈为空,元素无法出栈。\n");
return '\0';
}
char e = *(S.top - 1);
S.top--; //char e = *(--S.top);
return e;
}
int EmptyStack(SqStack& S)
{
if (S.base == S.top)
{
return 1;
}
else
return 0;
}
int getword(char* s, int limit)
{
int c = 0;
int i = 0;
for(i = 0;i<limit-1 &&(c = getchar()) != EOF && c != '\n';i++)
{
s[i] = c;
}
if (c == '\n')
{
s[i++] = c;
}
s[i] = '\0';
return i;
}
void Judgelegality(char * s)
{
SqStack S = { NULL,NULL,0 };
InitStack(S);
int i = 0;
char e = '\0';
while (s[i] != '\0')
{
if (s[i] == 'I')
{
Push(S, s[i]);
}
else if (s[i] == 'O')
{
if (EmptyStack(S))
{
printf("FALSE\n");
return;
}
e = Pop(S);
}
i++;
}
if (EmptyStack(S))
{
printf("TRUE\n");
}
else
{
printf("FALSE\n");
}
}
习题六(共三种方法,掌握一种即可)
假设以带头结点的循环链表表示队列,并且只设一个指针指向队尾元素结点 (注意:不设头指针),试编写相应的置空队列、判断队列是否为空、入队和出队等算法。
知识点回顾:
malloc函数:node *p=(node *)malloc(sizeof(node))
向内存申请一块大小为sizeof(node)的空间,并且返回指向这块空间的指针。
但是此时这个指针是一个未确定类型的指针void *,
因此需要把它强制转化为node *型的指针。
所以在malloc之前加上node *,这样等号右边就得到了一个node *的指针;
如果申请失败,会返回NULL.
结点:是数据元素a(i)的存储映像,包含两个域:数据域和指针域。
第一个结点(是结构类型):可能是头结点(不存储数据),也可能是首元结点(要存储数据)。
头结点:是在链表之前附设的一个结点,其指针域指向首元结点。
头结点的数据域可以不存储任何信息,也可存储与数据元素类型相同的其他附加信息(一般情况下都不存储数据。)
与“首元结点”区别开。
首元结点:是指链表中存储第一个数据元素a1(不是附加信息)的结点。
【设有头结点,则链表在初始化时,要定义一个新结点结构为头结点,并为其分配内存,且不往该头结点中存入数据。如:链队;
由于malloc函数的用法,为头结点分配内存后返回的是指向该头结点的的指针,该指针即为指向头结点的头指针。
链队中的头结点并没有专门的名称,只有指向其的头指针名称,但不影响访问。
以及链队头结点后面的每个结点,也并没有专门的名称,均通过指向其的指针名称访问、使用。
使用了malloc函数设置头结点的链表,一定也会有头指针。】
【不设有头结点,则链表的第一个结点为首元结点。在初始化时,无需单独为首元结点分配存储空间(压入数据时再创建新结点结构并分配内存,也是通过malloc函数返回指向新结点的指针),
只需要将指向首元结点的指针(即头指针)设为空指针。如链栈。
同样,链栈中的首元结点也并没有专门的名称,只有指向其的头指针名称,但不影响访问、使用。
以及链栈首元结点后面的每个结点,也并没有专门的名称,均通过指向其的指针名称访问、使用。】
头指针(是指针类型):始终指向链表中第一个结点的指针。
头指针可能指向的是头结点,也可能是首元结点。
【设头指针:初始化操作中,需定义一个新指针类型,为其分配内存,再将其指向第一个结点。
当链表中既有头结点又设有头指针时,如链队,为了设置其头结点,可以通过malloc函数,将等式右边直接设为指针类型。为头结点分配内存后,返回的该指针即为头指针。
当链表不设有头结点时,也不需要通过malloc函数,直接定义新指针类型,系统即会为其分配内存,定义后将其指向第一个结点即可。】
可由头指针唯一确定的单链表。若头指针名是L, 则简称该链表为表L.
因此一般情况下,这种链表的头指针名称已经在其存储结构定义typedef中,
及typedef之后的类型声明和类型转换中(包括函数的形式参数的类型定义)被定义出来,
并已被系统分配了内存,只需要将其指向链表中的第一个结点即可。
【尾结点:是存储链表中最后一个元素的结点。尾结点除指针域之外,在任何链表中,与除头结点之外的其它结点并无不同。
单链表中尾结点的指针域一般指向NULL,代表链表的结束。(与头结点的数据域和指针域均正好相反)。
在循环链表中,尾结点的指针域一般指向链表中第一个节点。
尾指针:与头指针相对应,始终指向链表中的最后一个结点,尾结点。
【注意:头结点和尾结点是有区别的,因此指向第一个结点为头结点的头指针,与尾指针也是有区别的。】
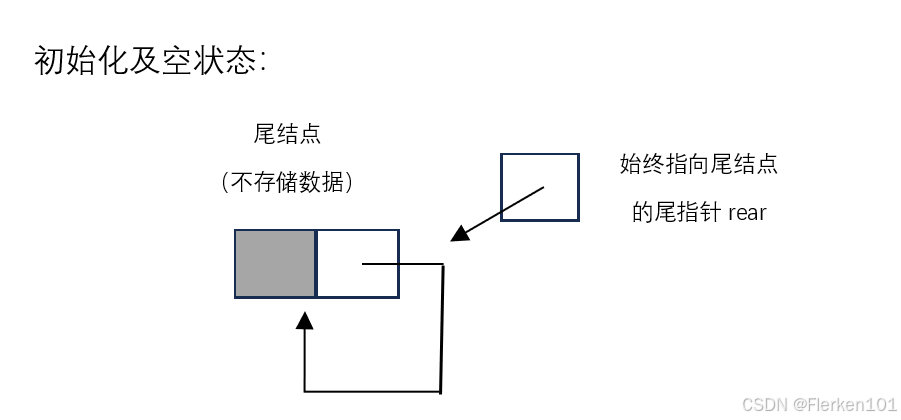
题目分析:
有头结点(第一个结点为头结点,头结点中不存储数据)
循环链表(表中最后一个结点的指针域指向头结点,整个链表形成一个环。)
不设头指针(没有始终指向第一个结点即头结点的指针。)
只设一个指针指向队尾元素结点,即有尾指针。
方法一
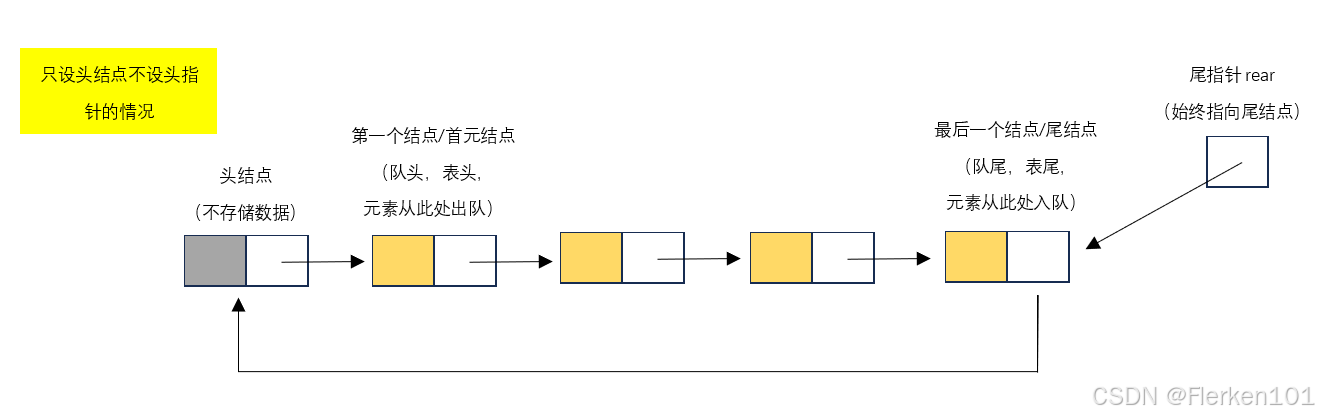
完全根据题目要求,其存储结构示意图为:
//代码
#include <stdio.h>
#include <stdlib.h>
typedef int SElemType;
typedef struct CirQueueNode
{
SElemType data;
struct CirQueueNode* next;
}CirQueueNode, * CQNodeptr;
typedef struct
{
CQNodeptr rear;
}CQLink;
void InitCQLink(CQLink& CQL);
void Push(CQLink& CQL, SElemType e);
SElemType Pop(CQLink& CQL);
int EmptyCQLink(CQLink& CQL);
void printCQLink(CQLink& CQL);
int main()
{
int num = 0;
int len = 0;
CQLink Q = { NULL };
InitCQLink(Q);
int i = 0;
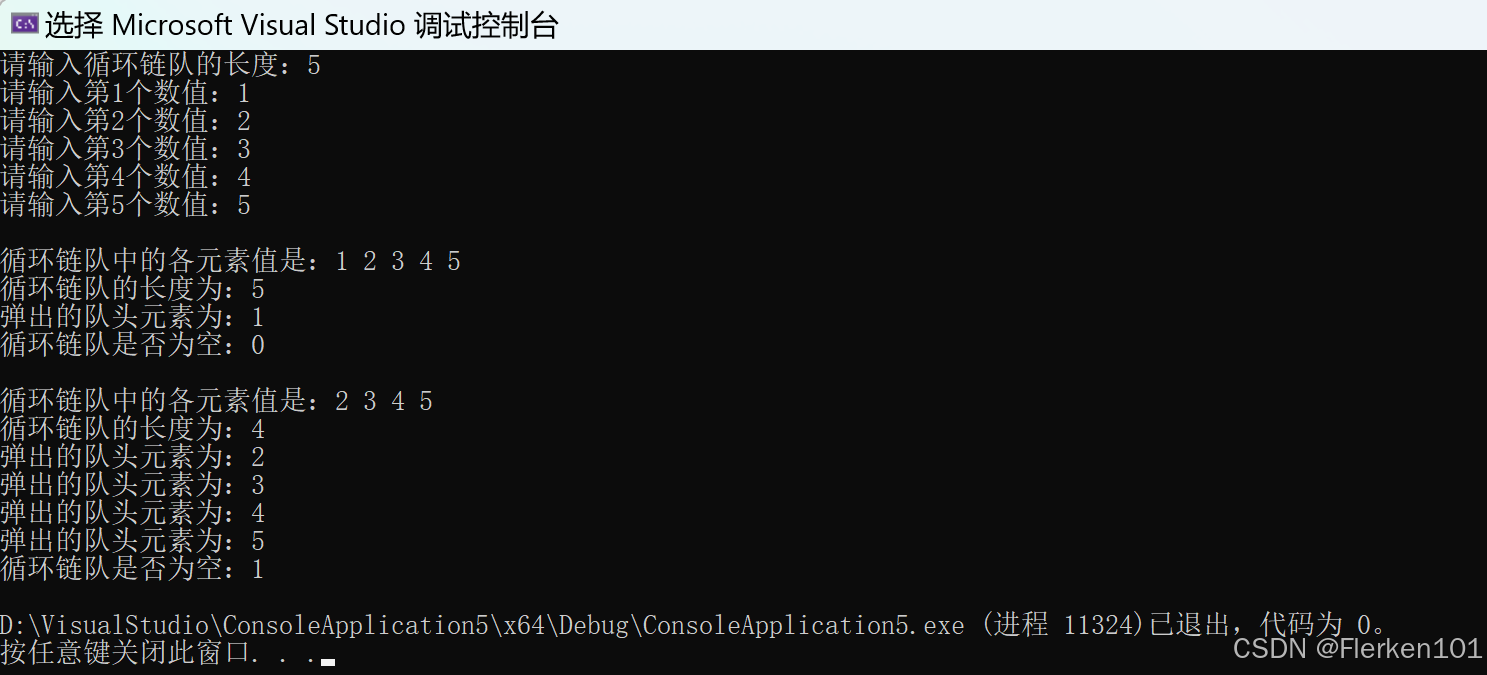
printf("请输入循环链队的长度:");
scanf_s("%d", &len);
for (i = 0; i < len; i++)
{
printf("请输入第%d个数值:", i + 1);
scanf_s("%d", &num);
Push(Q, num);
}
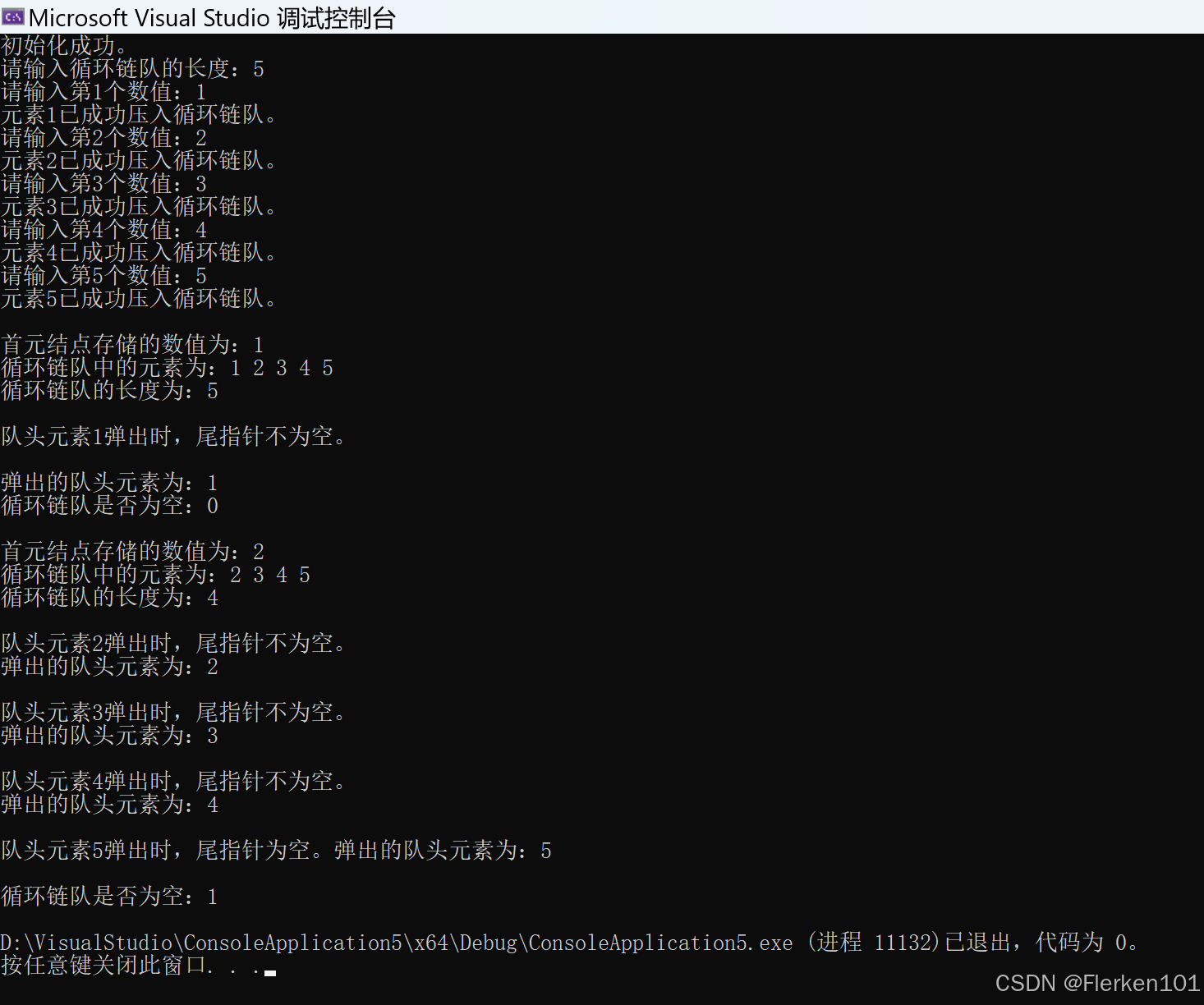
printCQLink(Q);
printf("\n弹出的队头元素为:%d", Pop(Q));
printf("\n循环链队是否为空:%d\n", EmptyCQLink(Q));
printCQLink(Q);
while (EmptyCQLink(Q) == 0)
{
printf("弹出的队头元素为:%d\n", Pop(Q));
}
printf("\n循环链队是否为空:%d\n", EmptyCQLink(Q));
return 0;
}
void InitCQLink(CQLink& CQL)
{
//为尾结点分配存储空间,因此产生的尾指针rear,正是可以唯一确定一个循环链队的尾结点
CQL.rear = (struct CirQueueNode*)malloc(sizeof(struct CirQueueNode));
//CQL中的访问头结点通过CQL.rear->next;访问第一个结点/首元结点通过CQL.rear->next->next;
if (!CQL.rear)
{
printf("尾结点及尾指针内存分配失败。\n");
return;
}
CQL.rear->data = -99999;
//为头结点分配存储空间,并将尾结点的指针域指向该头结点
struct CirQueueNode* p = NULL;
p = (struct CirQueueNode*)malloc(sizeof(struct CirQueueNode));
CQL.rear->next = p;
if (!CQL.rear->next)
{
printf("头结点内存分配失败。\n");
return;
}
//将头结点的指针域指向尾结点,形成一个循环链表(与空状态不同)
CQL.rear->next->next = CQL.rear;
printf("初始化成功。\n");
}
void Push(CQLink& CQL, SElemType e)
{
if (CQL.rear->data == -99999) //如果链表是初始化状态
{
CQL.rear->data = e;
}
else
{
//为新结点p分配存储空间
struct CirQueueNode* p = NULL;
p = (struct CirQueueNode*)malloc(sizeof(struct CirQueueNode));
if (!p)
{
printf("新结点内存分配失败。\n");
return;
}
p->data = e;
//新结点p成为尾结点,将该新结点p的指针域指向头结点
p->next = CQL.rear->next; //此处CQL.rear->next代表的是头结点
CQL.rear->next = p; //此处CQL.rear->next代表的是尾结点的指针域
//令尾指针指向该新结点p
CQL.rear = p;
}
printf("元素%d已成功压入循环链队。\n",e);
}
SElemType Pop(CQLink& CQL)
{
if (EmptyCQLink(CQL))
{
printf("弹出栈顶元素时,队列为空。\n");
return -999;
}
struct CirQueueNode* s = CQL.rear->next->next;
SElemType e = 0;
//删除的总是首元结点
if (s == CQL.rear) //当首元结点就是尾结点时
{
e = CQL.rear->data;
free(CQL.rear);
CQL.rear = NULL;
}
else
{
s = CQL.rear->next->next;
e = s->data;
CQL.rear->next->next = s->next;
free(s);
s = NULL;
}
if (CQL.rear == NULL)
{
printf(" \n队头元素%d弹出时,尾指针为空。",e);
}
else
{
printf(" \n队头元素%d弹出时,尾指针不为空。\n", e);
}
return e;
}
int EmptyCQLink(CQLink& CQL)
{
if (CQL.rear == NULL)
{
return 1; //为空
}
else
{
return 0;
}
}
void printCQLink(CQLink& CQL)
{
//令s指向首元结点
struct CirQueueNode* s = CQL.rear->next->next;
printf("\n首元结点存储的数值为:%d", s->data);
int i = 1;
printf("\n循环链队中的元素为:");
while (s != CQL.rear->next)
//当s指向头结点时,遍历完毕,跳出循环
{
printf("%d ", s->data);
s = s->next; //s一直向后移动
i++;
}
printf("\n循环链队的长度为:%d\n", i-1);
}
方法二
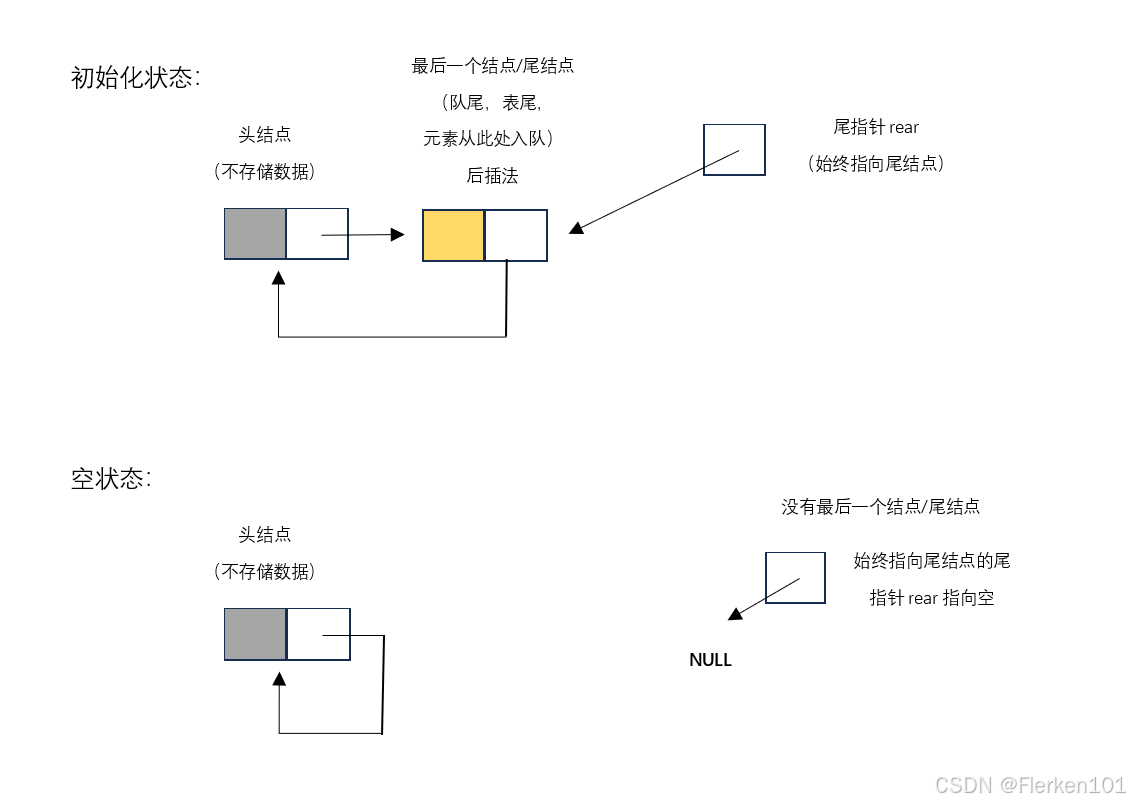
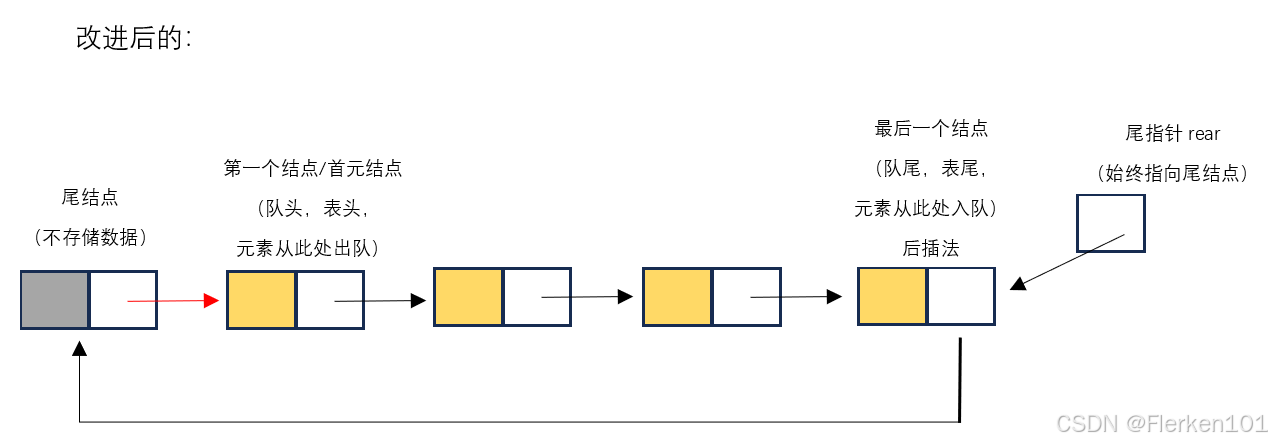
【题目共四个要求放在一起看:
分析其中三个要求:①有头结点,③没有头指针,④但是有尾指针。
尾指针本来是指向链表的最后一个结点,且最后一个结点的数据域本来还存有数据的,
但由于该头结点必须使用,因此张冠李戴,将该头结点改名为尾结点(不往该尾结点中存储数据),放在最后一个结点的后面,并让一个尾指针指向它。
(此处的尾结点、尾指针与平常意义上的尾结点、尾指针均不相同。
严格来说,没有满足题目中的①有头结点这个要求。但是利用了一个同样不存储数据的的尾结点,因此也可以说是设置了头结点,但是换了名称。)
还要求是循环链表:该将该尾结点指针域指向队头。 红色箭头。】
//改进后代码
#include <stdio.h>
#include <stdlib.h>
typedef int SElemType;
typedef struct CirQueueNode
{
SElemType data;
struct CirQueueNode* next;
}CirQueueNode,*CQNodeptr;
typedef struct
{
CQNodeptr rear;
}CQLink;
void InitCQLink(CQLink& CQL);
void Push(CQLink& CQL, SElemType e);
SElemType Pop(CQLink& CQL);
int EmptyCQLink(CQLink& CQL);
void printCQLink(CQLink& CQL);
int main()
{
int num = 0;
int len = 0;
CQLink Q = { NULL };
InitCQLink(Q);
int i = 0;
printf("请输入循环链队的长度:");
scanf_s("%d", &len);
for (i = 0; i < len; i++)
{
printf("请输入第%d个数值:", i + 1);
scanf_s("%d", &num);
Push(Q, num);
}
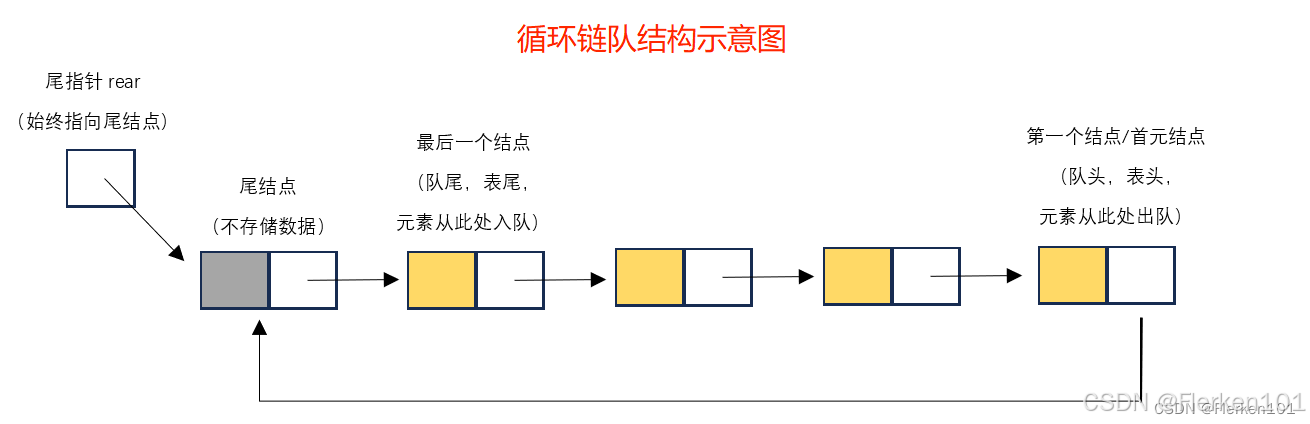
printCQLink(Q);
printf("\n弹出的队头元素为:%d", Pop(Q));
printf("\n循环链队是否为空:%d\n", EmptyCQLink(Q));
printCQLink(Q);
while (EmptyCQLink(Q) == 0)
{
printf("\n弹出的队头元素为:%d", Pop(Q));
}
printf("\n循环链队是否为空:%d\n", EmptyCQLink(Q));
return 0;
}
void InitCQLink(CQLink& CQL)
{
CQL.rear = (struct CirQueueNode*)malloc(sizeof(struct CirQueueNode));
if (!CQL.rear)
{
printf("内存分配失败!\n");
return;
}
CQL.rear->next = CQL.rear;
}
void Push(CQLink& CQL, SElemType e)
{
struct CirQueueNode* p = (struct CirQueueNode*)malloc(sizeof(struct CirQueueNode));
if (!p)
{
printf("内存分配失败!\n");
return;
}
p->data = e;
struct CirQueueNode* q = CQL.rear->next;
if (q == CQL.rear) //还在初始化及空状态
{
p->next = CQL.rear;
CQL.rear->next = p;
}
else
{
while (q->next != CQL.rear)
{
q = q->next;
}
//q指向了最后一个结点
p->next = CQL.rear;
q->next = p;
}
}
SElemType Pop(CQLink& CQL)
{
if (CQL.rear->next == CQL.rear)
{
printf("弹出队头元素时,循环链队为空。\n");
return -9999;
}
struct CirQueueNode* q = CQL.rear->next;
SElemType e = q->data;
CQL.rear->next = q->next;
free(q);
q = NULL;
return e;
}
int EmptyCQLink(CQLink& CQL)
{
if (CQL.rear->next == CQL.rear)
{
return 1;
}
else
{
return 0;
}
}
void printCQLink(CQLink& CQL)
{
int i = 0;
struct CirQueueNode* q = CQL.rear->next;
if(EmptyCQLink(CQL))
{
printf("打印元素时,循环链队为空。\n");
return;
}
printf("\n循环链队中的各元素值是:");
while (q != CQL.rear)
{
printf("%d ", q->data);
i++;
q = q->next;
}
printf("\n循环链队的长度为:%d", i);
}
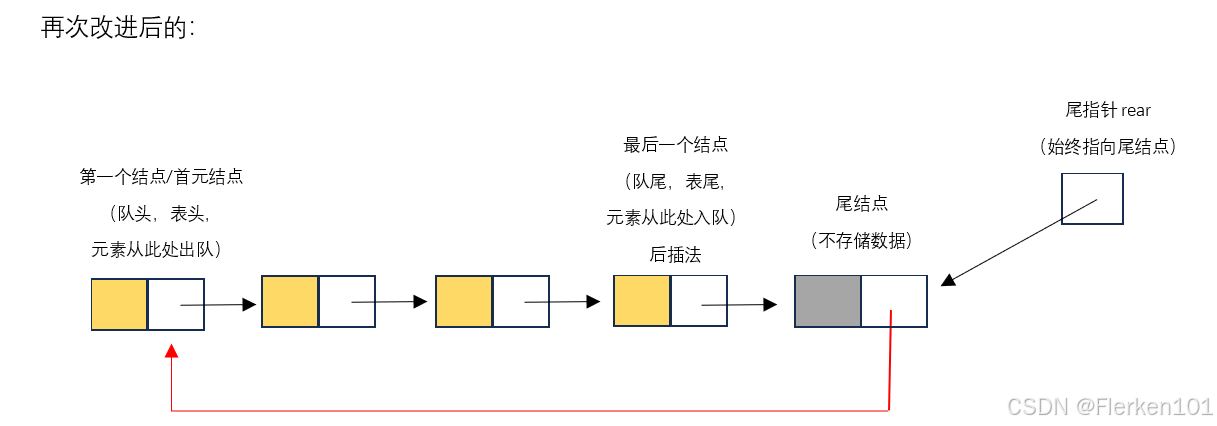
方法三
第三种实现方式及代码:
//代码
//循环链队(循环队列的链式结构,链队的循环链表结构)
#include <stdio.h>
#include <stdlib.h>
#define MAXLEN 100
typedef int SElemType;
typedef struct CirQueueNode
{
SElemType data;
struct CirQueueNode* next;
}CirQueueNode, * CQNodeptr;
typedef struct
{
CQNodeptr rear;
}CQLink;
void InitCQLink(CQLink& CQL);
void Push(CQLink& CQL, SElemType e);
SElemType Pop(CQLink& CQL);
int EmptyCQLink(CQLink& CQL);
void printCQLink(CQLink& CQL);
int main()
{
int num = 0;
int len = 0;
CQLink Q = { NULL };
InitCQLink(Q);
int i = 0;
printf("请输入循环链队的长度:");
scanf_s("%d", &len);
for (i = 0; i < len; i++)
{
printf("请输入第%d个数值:", i + 1);
scanf_s("%d", &num);
Push(Q, num);
}
printCQLink(Q);
printf("\n弹出的队头元素为:%d", Pop(Q));
printf("\n循环链队是否为空:%d\n", EmptyCQLink(Q));
printCQLink(Q);
while (EmptyCQLink(Q) == 0)
{
printf("\n弹出的队头元素为:%d", Pop(Q));
}
printf("\n循环链队是否为空:%d\n", EmptyCQLink(Q));
return 0;
}
//初始化
void InitCQLink(CQLink& CQL)
{
CQL.rear = (CQNodeptr)malloc(sizeof(struct CirQueueNode)); //头结点
CQL.rear->next = CQL.rear; //尾指针的下一个还是自己,空链队形成自循环
}
//入队(表尾在队尾(入),表头在队头(出))
void Push(CQLink& CQL, SElemType e)
{
struct CirQueueNode* p = (CQNodeptr)malloc(sizeof(struct CirQueueNode));
if (!p)
{
printf("内存分配失败!\n");
return;
}
p->data = e;
p->next = CQL.rear->next;
CQL.rear->next = p;
}
//出队
SElemType Pop(CQLink& CQL)
{
if (CQL.rear == CQL.rear->next)
{
printf("队列为空,元素无法出队。\n");
return 0;
}
CQNodeptr q = CQL.rear;
CQNodeptr p = CQL.rear->next;
while (p->next != CQL.rear)
{
q = p;
p = p->next; //p达到队头
}
SElemType e = p->data;
q->next = p->next;
free(p);
return e;
}
//判空
int EmptyCQLink(CQLink& CQL)
{
if (CQL.rear == CQL.rear->next)
{
printf("\n循环链队为空。");
return 1;
}
else
{
printf("\n循环链队不为空。");
return 0;
}
}
void printCQLink(CQLink& CQL)
{
int i = 0;
int s[MAXLEN];
struct CirQueueNode* q = CQL.rear->next;
if(EmptyCQLink(CQL))
{
printf("打印元素时,循环链队为空。\n");
return;
}
while (q != CQL.rear)
{
s[i] = q->data;
i++;
q = q->next;
}
printf("\n循环链队的长度为:%d", i);
i--;
printf("\n循环链队中的各元素值是:");
while (i >= 0 )
{
printf("%d ", s[i]);
i--;
}
}
习题七
假设以数组Q[m]存放循环队列中的元素,同时设置一个标志tag, 以 tag == 0 和 tag == 1 来区别在队头指针 (front) 和队尾指针 (rear) 相等时,队列状态为“空” 还是 “满” 。试编写与此结构相应的插入 (enqueue) 和删除 (dequeue) 算法。
#include <stdio.h>
#include <stdlib.h>
#define m 10 //数组Q中可以存储的最多数值
typedef int SElemType;
typedef struct
{
SElemType* Q;
int front;
int rear;
int tag;
}SqQueue;
void InitSqQue(SqQueue& S);
void EnQueue(SqQueue& S, SElemType e);
SElemType DeQueue(SqQueue& S);
int EmptySqQueue(SqQueue& S);
int FullSqQueue(SqQueue& S);
void printSqQueue(SqQueue& S);
int main()
{
int i = 0;
SqQueue N = { NULL,0,0,0 };
InitSqQue(N);
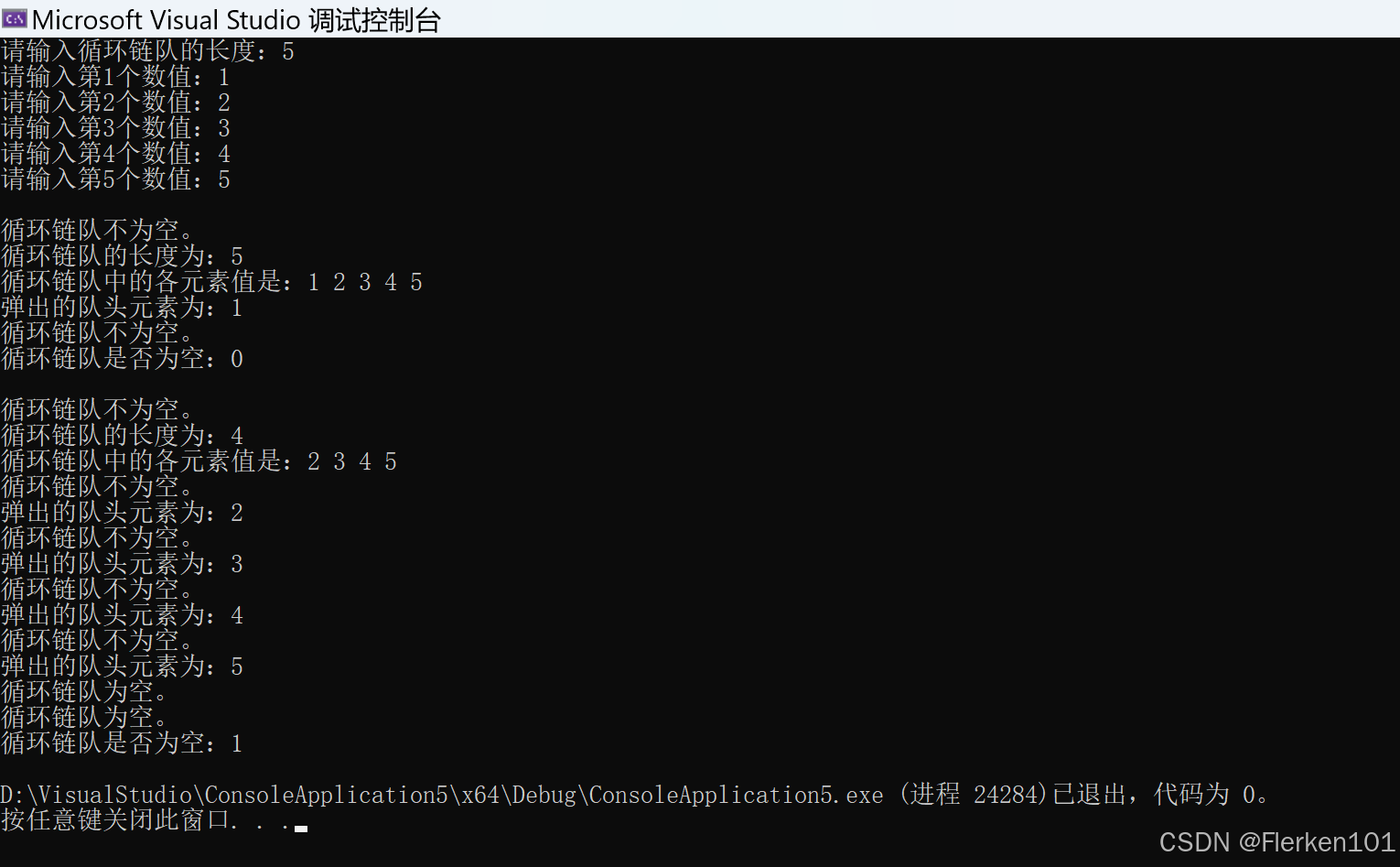
printf("EmptySqQueue : %d\n", EmptySqQueue(N));
for (i = 1; i <=10 ; i++)
{
EnQueue(N, i);
}
printf("FullSqQueue : %d\n", FullSqQueue(N));
//上面已经执行过EmptySqQueue函数,其计算值为1.
// 此处在printSqQueue若判空条件使用EmptySqQueue函数,则直接返回其值1
printSqQueue(N);
printf("DeQueue : %d\n", DeQueue(N));
printSqQueue(N);
return 0;
}
//初始化
void InitSqQue(SqQueue& S)
{
S.Q = (SElemType*)malloc(sizeof(SElemType) * m);
if (!S.Q)
{
printf("内存分配失败,初始化失败。\n");
return;
}
S.front = S.rear = 0;
S.tag = 0;
}
//插入
void EnQueue(SqQueue& S, SElemType e)
{
if (S.front == S.rear && S.tag == 1)
{
printf("入队时,队列已满。\n");
return;
}
S.Q[S.rear] = e;
S.rear = (S.rear + 1) % m;
//每次插入动作执行完之后,此处同牺牲一个内存空间的情况一样,队尾指针S.rear仍然指向的是队尾元素的后面的空位置
//因此队列中元素的个数/长度仍然是(S.rear - S.front + m) % m
//当且仅当将队列存储满时,两者之间才有区别。
if (S.rear == S.front)
{
S.tag = 1;
}
}
//删除
SElemType DeQueue(SqQueue& S)
{
if (S.front == S.rear && S.tag == 0)
{
printf("出队时,队列为空。\n");
return 0;
}
SElemType e = S.Q[S.front];
S.front = (S.front + 1) % m;
if (S.rear == S.front)
{
S.tag = 0;
}
return e;
}
int EmptySqQueue(SqQueue& S)
{
if (S.front == S.rear && S.tag == 0)
{
printf("队列为空。\n");
return 1;
}
else
{
return 0;
}
}
int FullSqQueue(SqQueue& S)
{
if (S.front == S.rear && S.tag == 1)
{
printf("队列已满。\n");
return 1;
}
else
{
return 0;
}
}
void printSqQueue(SqQueue& S)
{
int i = 0;
int temp = S.front; //i与长度相关,temp才与存储数据的下标相关。
printf("S.front = %d\n", S.front);
printf("S.rear = %d\n", S.rear); //队尾指针S.rear仍然指向的是队尾元素的后面的空位置
printf("(S.rear - S.front + m) % m = %d\n", (S.rear - S.front + m) % m);
if (S.front == S.rear && S.tag == 0)
//必须用这个语句,而不能用EmptySqQueue函数,原因见主函数
{
printf("打印队列时,队列为空。\n");
return;
}
printf("\n队列中的元素为:");
//当队列满时的打印
if (S.front == S.rear && S.tag == 1)
{
for (i = 0; i < m; i++)
//i与长度相关,temp才与存储数据的下标相关。
{
printf("%d ", S.Q[temp]);
temp = (temp + 1) % m;
}
}
else
{
for (i = 0; i < ((S.rear - S.front + m) % m); i++)
//判断条件不能使用i != S.rear,会多输出一个乱码。
//在此处队列也是用环状的一维循环数组存储的,但是没有牺牲的一个存储空间。
//但队尾指针S.rear仍然指向的是队尾元素的后面的空位置,所以在没有储存满的情况下,这里同牺牲的一个存储空间时打印的写法一样。
{
printf("%d ", S.Q[temp]);
temp = (temp + 1) % m;
}
}
printf("\nQueue_length : %d\n", i);
}
习题八
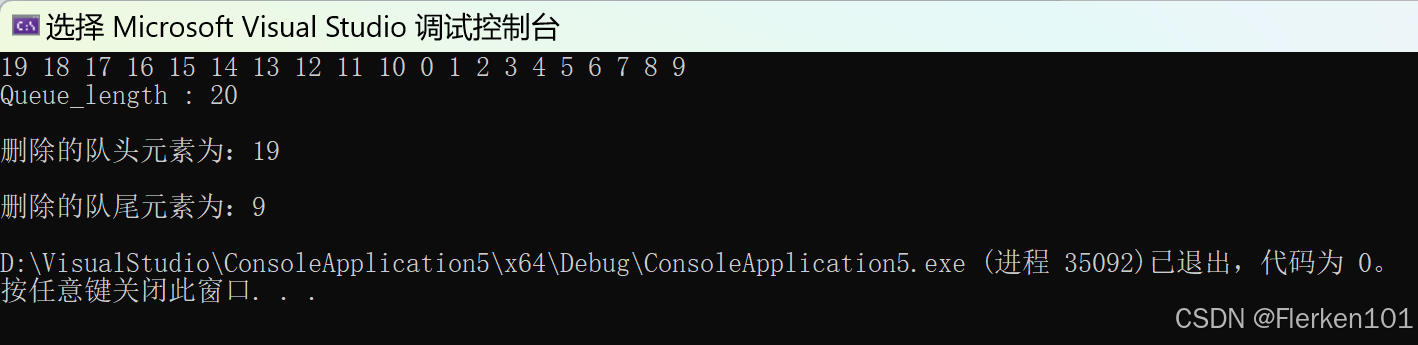
如果允许在循环队列的两端都可以进行插入和删除操作。要求:
① 写出循环队列的类型定义;
② 写出“从队尾删除” 和 “从队头插入” 的算法。
传统上的循环队列:
元素的存储顺序/Q.front、Q.rear的移动顺序是:沿着从队头Q.front到队尾Q.rear的顺时针方向。
元素从队头出,Q.front依环状加1,Q.front= (Q.front+1)%MAXQSIZE;
元素从队尾进,Q.rear依环状加1,Q.rear= (Q.rear+1)%MAXQSIZE.
此处的循环列队,两端都可以进行元素的插入和删除。
因此是在保留了上面传统循环列队性质的基础上,增加了:
元素的存储顺序/Q.front、Q.rear的移动顺序是:沿着从队尾Q.rear到队头Q.front的逆时针方向。(这样才能保证与上面的情况,在元素中存储数据的位置是相同的。)
元素从队头进,Q.front依环状减1,Q.front= (Q.front-1) % MAXQSIZE;
元素从队尾出,Q.rear依环状减1,Q.rear= (Q.rear-1) % MAXQSIZE;
#include <stdio.h>
#include <stdlib.h>
#define MAXQSIZE 100
typedef int SElemType;
typedef struct
{
SElemType* base;
int front;
int rear;
}SqQueue;
void InitQueue(SqQueue& Q);
void printQueue(SqQueue& Q);
void EnQueueRear(SqQueue& Q, SElemType e);
SElemType DeQueueFront(SqQueue& Q);
SElemType DeQueRear(SqQueue& Q);
void EnQueFront(SqQueue& Q, SElemType e);
int main()
{
SqQueue M = { NULL,0,0 };
InitQueue(M);
int i = 0;
int j = 10;
for (i = 0; i < 10; i++)
{
EnQueueRear(M, i);
}
for (j = 10; j < 20; j++)
{
EnQueFront(M, j);
}
printQueue(M);
printf("\n删除的队头元素为:%d\n", DeQueueFront(M));
printf("\n删除的队尾元素为:%d\n", DeQueRear(M));
return 0;
}
void InitQueue(SqQueue& Q)
{
Q.base = (SElemType*)malloc(sizeof(SElemType) * MAXQSIZE);
if (!Q.base)
{
printf("内存分配失败,导致初始化循环队列失败。");
return;
}
Q.front = 0;
Q.rear = 0;
}
void printQueue(SqQueue& Q)
{
//在此处的循环列表中,队列的长度仍为(Q.rear - Q.front + MAXQSIZE) % MAXQSIZE
int i = 0;
int temp = Q.front;
if (Q.front == Q.rear)
{
printf("打印循环队列时,队列为空。\n");
return;
}
for (i = 0; i < ((Q.rear - Q.front + MAXQSIZE) % MAXQSIZE); i++)
{
printf("%d ", Q.base[temp]); //假设总是从队头开始打印
temp = (temp + 1) % MAXQSIZE;
}
printf("\nQueue_length : %d\n", i);
}
//从队尾插入
void EnQueueRear(SqQueue& Q, SElemType e)
{
//插入元素e为Q的新的队尾元素
if ((Q.rear + 1) % MAXQSIZE == Q.front)
{
printf("从队尾入队时,循环队列已满。\n");
return;
}
Q.base[Q.rear] = e;
Q.rear = (Q.rear + 1) % MAXQSIZE;
}
//从队头删除
SElemType DeQueueFront(SqQueue& Q)
{
//删除Q的队头元素
int e = 0;
if (Q.front == Q.rear)
{
printf("从队头删除元素时,循环队列为空。\n");
return -1;
}
e = Q.base[Q.front];
Q.front = (Q.front + 1) % MAXQSIZE;
return e;
}
//以下是增加的两个功能
//从队尾删除
SElemType DeQueRear(SqQueue& Q)
{
if (Q.front == Q.rear)
{
printf("从队尾删除元素时,循环队列为空。\n");
return 0;
}
Q.rear = (Q.rear - 1) % MAXQSIZE;
SElemType e = Q.base[Q.rear];
//队尾Q.rear仍然指向的是队列中最后一个元素的下一个位置,其本身所在的位置默认没有存储任何数据
return e;
}
//从队头插入
void EnQueFront(SqQueue& Q, SElemType e)
{
if ((Q.front - 1) % MAXQSIZE == Q.rear)
{
printf("从队头插入元素时,循环队列已满。\n");
return;
}
Q.front = (Q.front - 1 + MAXQSIZE) % MAXQSIZE;
//当原Q.front为0时,不能使Q.front变为负值,依环状减1,应变为最大坐标值
Q.base[Q.front] = e;
}
递归知识点回顾
当 定义是递归的 和 数据结构是递归的 时,采用“分治法” 求解递归问题。P64
习题九(定义是递归的)
已知Ackermann 函数定义如下:
① 写出计算Ack(m,n)的递归算法,并根据此算法给出Ack(2,1)的计算过程。
② 写出计算Ack(m,n)的非递归算法。
//Ack(m,n)的递归算法
#include <stdio.h>
int Ack(int m, int n);
int main()
{
int r = 0;
r = Ack(2, 1);
printf("r = %d", r);
return 0;
}
int Ack(int m, int n)
{
int result = 0;
if (m == 0)
{
result = n + 1;
}
else if(m != 0 && n == 0)
{
result = Ack(m - 1, 1);
}
else
{
result = Ack(m - 1, Ack(m ,n -1));
}
return result;
}
【 第7/8关:Ackermann函数的递归求值/非递归求值】【头歌 bjfu-249 250】 ————汤米尼克
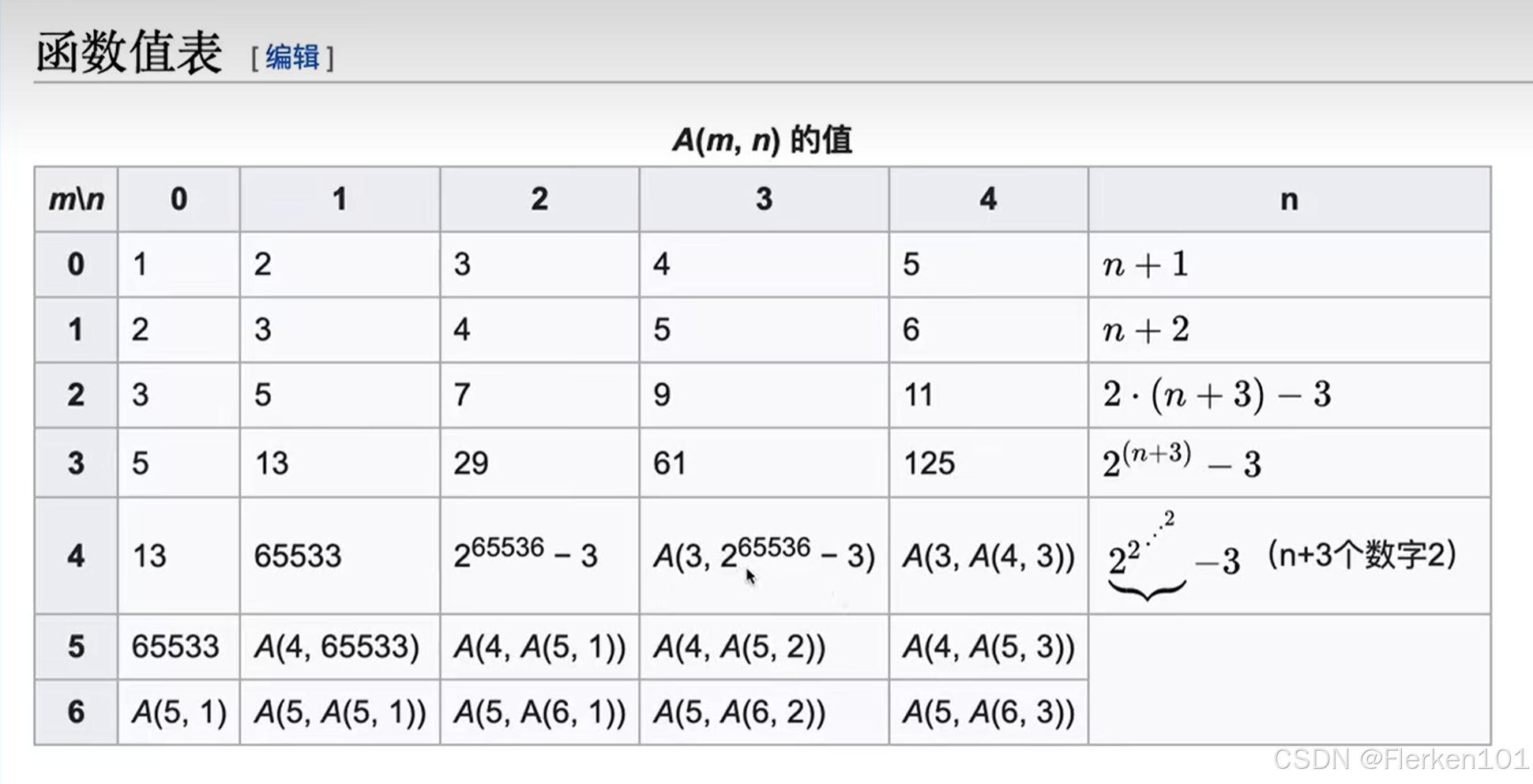
下表是阿克曼函数的函数值,即阿克曼函数对应的矩阵中每个坐标处的值。
阿克曼函数的作用:用两个很小的数得出一个很大很大的数。
当m≥4,Ackermann函数的增长就快得惊人。
//Ack(m,n)的非递归算法
#include <stdio.h>
#include <iostream>
using namespace std;
#define MAXSIZE 100
int Ack(int m, int n);
int main()
{
int m, n;
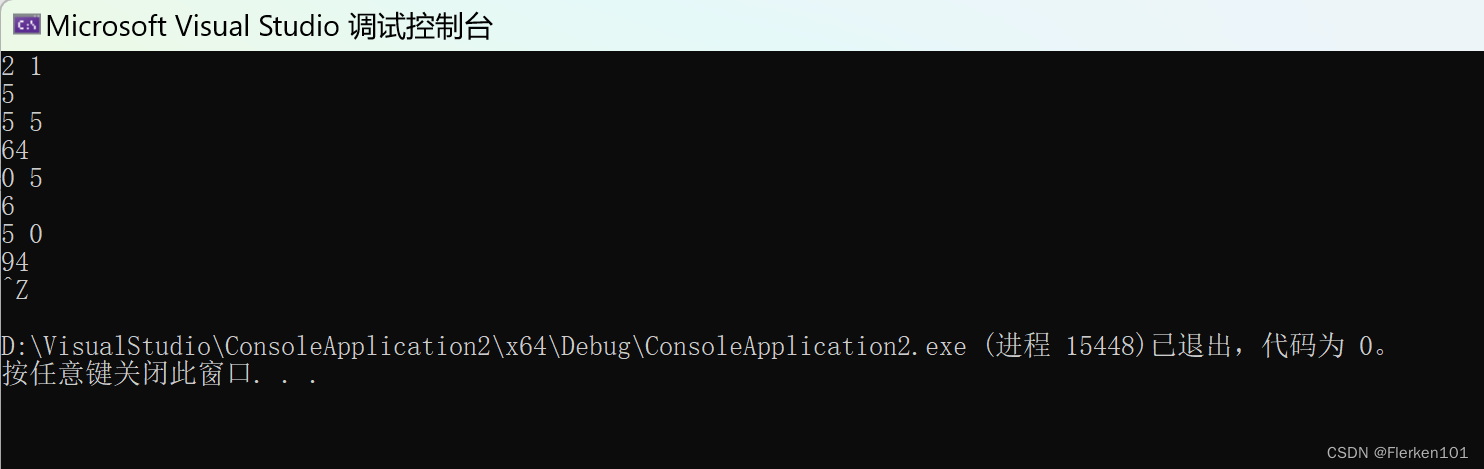
while (cin >> m >> n)
{
if (m == 0 && n == 0) break;
cout << Ack(m, n) << endl;
}
return 0;
}
int Ack(int m, int n)
{//Ackermann函数的非递归求值
int tmp[MAXSIZE][MAXSIZE];
for (int j = 0; j < MAXSIZE; j++)
tmp[0][j] = j + 1;
for (int i = 1; i <= m; i++)
{
tmp[i][0] = tmp[i - 1][1];
for (int j = 1; j < MAXSIZE; j++)
//填充剩余矩阵项
tmp[i][j] = tmp[i - 1][tmp[i][j - 1]];
}
return (tmp[m][n]);
}
习题十(数据结构是递归的)
已知 f 为单链表的表头指针,链表中存储的都是整型数据,试写出实现下列运算的递归算法:
① 求链表中的最大整数;
② 求链表的结点个数;
③ 求所有整数的平均值。
#include <stdio.h>
#include <stdlib.h>
typedef struct Node
{
int data;
struct Node* next;
}LNode,*Link;
void InitLink(Link& L);
void Push(Link& L, int e);
void printLink(Link& L);
int maxLink(Link& L);
int mumLink(Link& L);
int avgLink(Link& L);
int main()
{
Link F = NULL;
InitLink(F);
for (int i = 1; i <= 10; i++)
{
Push(F, i);
}
printLink(F);
printf("\n元素最大值为:%d\n", maxLink(F));
printf("元素个数为:%d\n", mumLink(F));
printf("元素平均值为:%d\n", avgLink(F));
return 0;
}
void InitLink(Link& L)
{
L = (struct Node*)malloc(sizeof(struct Node));
L->next = NULL;
}
//头插法
void Push(Link& L,int e)
{
struct Node* p = (struct Node*)malloc(sizeof(struct Node));
p->data = e;
p->next = L->next;
L->next = p;
}
//打印链表中的元素
void printLink(Link& L)
{
if (!L)
{
printf("打印链表中元素时,单链表为空。\n");
return;
}
struct Node* p = L->next;
printf("单链表中元素为:");
while (p)
{
printf(" %d", p->data);
p = p->next;
}
}
//①求链表中的最大整数
int maxLink(Link &L)
{
struct Node* q = L->next;
struct Node* p = q->next;
int m = q->data;
while (p)
{
if (m < p->data)
{
m = p->data;
}
q = p;
p = p->next;
}
return m;
}
//②求链表的结点个数
int mumLink(Link& L)
{
if (!L)
{
printf("求结点个数时,单链表为空。\n");
return 0;
}
int num = 0;
struct Node* p = L->next;
while (p)
{
num++;
p = p->next;
}
return num;
}
//③求所有整数的平均值
int avgLink(Link& L)
{
int avg = 0;
int sum = 0;
int num = 0;
struct Node* p = L->next;
while (p)
{
sum = sum + p->data;
p = p->next;
}
if ((num = mumLink(L)) != 0)
{
avg = sum / num;
}
return avg;
}