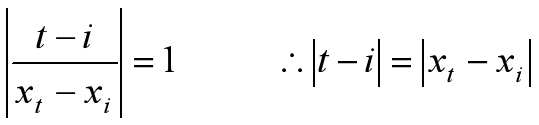【问题描述】

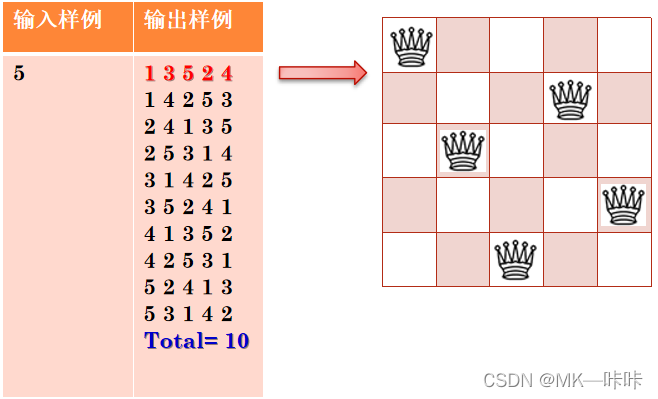
在n×n格的棋盘上放置彼此不受攻击的n个皇后。

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。n皇后问题等价于在n×n格的棋盘上放置n个皇后，任何两个皇后不放在同一行或同一列或同一斜线上。

编程要求：找出一个n×n格的棋盘上放置n个皇后并使其不能互相攻击的所有方案。

【算法分析】

由于棋盘的每列只有一个皇后，所以可以用一维向量X( x1, x2, …, xn)，其中xi∈{1, 2, …, n}，表示第i列皇后所在的行x[i]，即解空间的每个结点都有n个儿子，因此解空间的大小为n的n次方，这是一棵子集树。【算法分析】

【代码部分】

//n皇后问题回溯算法的数据结构
#define NUM 20
int n;			//棋盘的大小
int x[NUM];		//解向量
int sum;		//当前已经找到的可行方案数

//N皇后问题回溯算法的实现
//形参t是回溯的深度，从1开始
void Backtrack(int t) 
{ 
　　int i;
　　//到达叶子结点，获得一个可行方案。累计总数，并输出该方案
　　if (t>n) 
　　{
　　　　sum++;		//是全局变量
　　　　for (i=1; i<=n; i++) 
　　　　　　printf(" %d", x[i]);
　　　　printf("\n");
　　}
　　else
　　　　for (i=1; i<=n; i++) 
　　　　{
　　　　　　x[t] = i;
　　　　　　if (Place(t)) Backtrack(t+1);
　　　　}
}

//检查当前皇后位置的约束函数
//形参t是回溯的深度
inline bool Place(int t) 
{ 
　　int i; 
　　for (i=1; i<t; i++) 
　　　　if ((abs(t-i) == abs(x[i]-x[t])) || (x[i] == x[t])) 
　　　　　　return false; 
　　return true; 
}

由于每一列只放置一个皇后，所以不用判断合法性。

对于每一行，假设已经放置到t列，只要判断 ，i＝1, 2, …, t-1互不相同即可。

对于对角线的判断，可以看成是斜率为±1的两条直线，经过两点（i，x[i]）和（t，x[t]）:

//算法的完整实现
#include <iostream> 
#include <cmath>
using namespace std;

#define NUM 20
int n;
int x[NUM]; 
int sum; 

inline bool Place(int t) 
{ 
	int i; 
	for (i=1; i<t; i++) 
		if ((abs(t-i) == abs(x[i]-x[t])) || (x[i] == x[t])) 
			return false; 
	return true; 
} 

void Backtrack(int t) 
{ 
	int i;
	if (t>n) 
	{
		sum++;
		for (i=1; i<=n; i++) 
			printf(" %d", x[i]);
		printf("\n");
	}
	else
		for (i=1; i<=n; i++) 
		{
			x[t] = i;
			if (Place(t)) Backtrack(t+1);
		}
} 

int main() 
{ 
	while (cin>>n)
	{
		sum = 0;
		Backtrack(1);
		printf("Total= %d\n\n", sum);
	}
	return 0; 
}