Java碰撞的小球

问题描述

　　数轴上有一条长度为L（L为偶数)的线段，左端点在原点，右端点在坐标L处。有n个不计体积的小球在线段上，开始时所有的小球都处在偶数坐标上，速度方向向右，速度大小为1单位长度每秒。
　　当小球到达线段的端点（左端点或右端点）的时候，会立即向相反的方向移动，速度大小仍然为原来大小。
　　当两个小球撞到一起的时候，两个小球会分别向与自己原来移动的方向相反的方向，以原来的速度大小继续移动。
　　现在，告诉你线段的长度L，小球数量n，以及n个小球的初始位置，请你计算t秒之后，各个小球的位置。

提示

　　因为所有小球的初始位置都为偶数，而且线段的长度为偶数，可以证明，不会有三个小球同时相撞，小球到达线段端点以及小球之间的碰撞时刻均为整数。
　　同时也可以证明两个小球发生碰撞的位置一定是整数（但不一定是偶数）。

输入格式

　　输入的第一行包含三个整数n, L, t，用空格分隔，分别表示小球的个数、线段长度和你需要计算t秒之后小球的位置。
　　第二行包含n个整数a1, a2, …, an，用空格分隔，表示初始时刻n个小球的位置。

输出格式

　　输出一行包含n个整数，用空格分隔，第i个整数代表初始时刻位于ai的小球，在t秒之后的位置。

样例输入

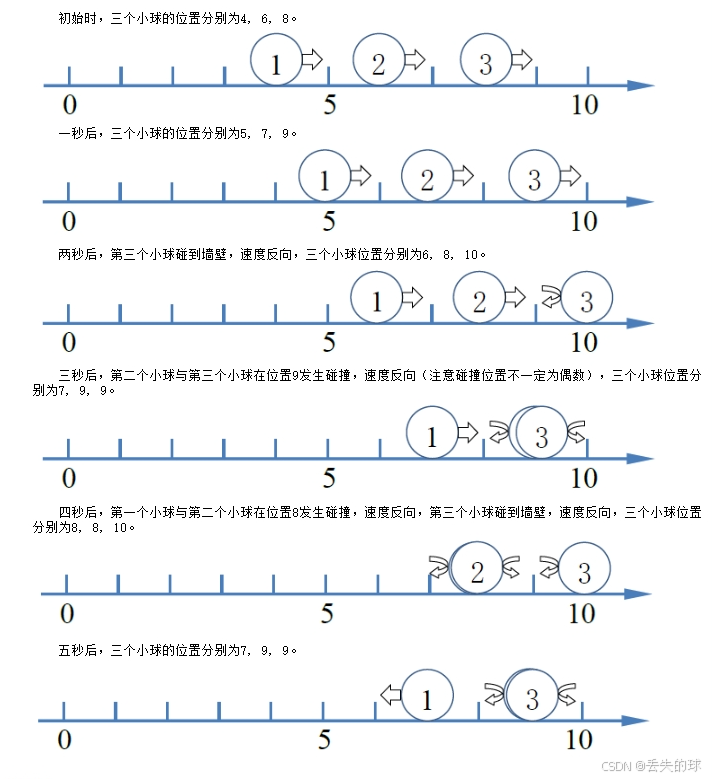
3 10 5
4 6 8

样例输出

7 9 9

样例说明

样例输入

10 22 30
14 12 16 6 10 2 8 20 18 4

样例输出

6 6 8 2 4 0 4 12 10 2

数据规模和约定

　　对于所有评测用例，1 ≤ n ≤ 100，1 ≤ t ≤ 100，2 ≤ L ≤ 1000，0 < ai < L。L为偶数。
　　保证所有小球的初始位置互不相同且均为偶数。


import java.util.Scanner;

public class MainBall {
    public static void main(String[] args) {
        Scanner scanner=new Scanner(System.in);
        int n= scanner.nextInt();
        int L= scanner.nextInt();
        int time= scanner.nextInt();
        Ball[] balls=new Ball[n];

        for (int i=0;i<n;i++){//输入小球位置，以及确定初始方向
            int pos= scanner.nextInt();
            balls[i]=new Ball(pos,1);
        }

        for (int t=0;t<time;t++){//规定时间内，小球位置以及方向变化，小球是否碰撞到边缘
            for (int i=0;i<n;i++){
                if (balls[i].direction==1){
                    balls[i].postion++;
                    if (balls[i].postion==L){
                        balls[i].direction*=-1;
                    }
                }
                else {
                    balls[i].postion--;
                    if (balls[i].postion==0){
                        balls[i].direction*=-1;
                    }
                }
            }

            for (int i=0;i<n-1;i++){//小球是否碰撞，以及碰撞后变化
                for (int j=i+1;j<n;j++){
                    if (balls[i].postion==balls[j].postion){
                        balls[i].direction*=-1;
                        balls[j].direction*=-1;
                        break;//三个球一定不会同时碰撞
                    }
                }
            }
        }
        for (int i=0;i<n;i++){
            System.out.print(balls[i].postion+" ");
        }
    }
}

Java碰撞的小球

悦读