写在前面
Canny边缘检是在在1986年提出来的,到今天已经30多年过去了,但Canny算法仍然是图像边缘检测算法中最经典、先进的算法之一。
相比Sobel、Prewitt等算子,Canny算法更为优异。Sobel、Prewitt等算子有如下缺点:
- 没有充分利用边缘的梯度方向。
- 最后得到的二值图,只是简单地利用单阈值进行处理。
而Canny算法基于这两点做了改进,提出了:
- 基于边缘梯度方向的非极大值抑制。
- 双阈值的滞后阈值处理。
原理
从表面效果上来讲,Canny算法是对Sobel、Prewitt等算子效果的进一步细化和更加准确的定位。
Canny算法基于三个基本目标:
- 低错误率。所有边缘都应被找到,且没有伪响应。
- 边缘点应该被很好地定位。已定位的边缘必须尽可能接近真实边缘。
- 单一的边缘点响应。这意味在仅存一个单一边缘点的位置,检测器不应指出多个像素边缘。
进而,Canny的工作本质是,从数学上表达前面的三个准则。因此Canny的步骤如下:
- 对输入图像进行高斯平滑,降低错误率。
- 计算梯度幅度和方向来估计每一点处的边缘强度与方向。
- 根据梯度方向,对梯度幅值进行非极大值抑制。本质上是对Sobel、Prewitt等算子结果的进一步细化。
- 用双阈值处理和连接边缘。
详细步骤
1、高斯平滑(略)
2、计算梯度幅度和方向
可选用的模板:soble算子、Prewitt算子、Roberts模板等等;
一般采用soble算子,OpenCV也是如此,利用soble水平和垂直算子与输入图像卷积计算dx、dy:
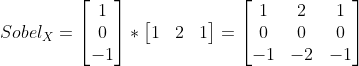
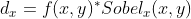
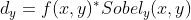
进一步可以得到图像梯度的幅值:
为了简化计算,幅值也可以作如下近似:
角度为:
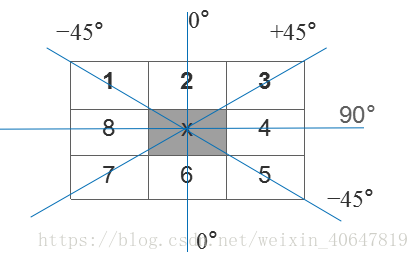
如下图表示了中心点的梯度向量、方位角以及边缘方向(任一点的边缘与梯度向量正交) :
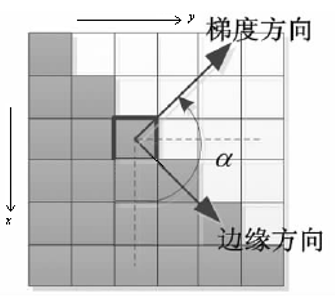
3、根据角度对幅值进行非极大值抑制
划重点:是沿着梯度方向对幅值进行非极大值抑制,而非边缘方向,这里初学者容易弄混。
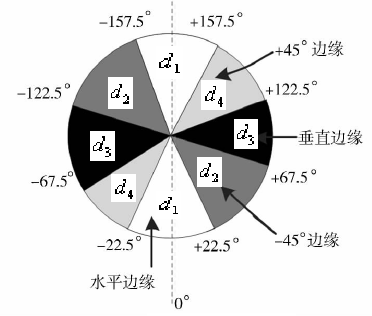
例如:3*3区域内,边缘可以划分为垂直、水平、45°、135°4个方向,同样,梯度反向也为四个方向(与边缘方向正交)。因此为了进行非极大值,将所有可能的方向量化为4个方向,如下图:
量化化情况可总结为:
- 水平边缘--梯度方向为垂直:
- 135°边缘--梯度方向为45°:
- 垂直边缘--梯度方向为水平:
- 45°边缘--梯度方向为135°:
非极大值抑制即为沿着上述4种类型的梯度方向,比较3*3邻域内对应邻域值的大小:
在每一点上,领域中心 x 与沿着其对应的梯度方向的两个像素相比,若中心像素为最大值,则保留,否则中心置0,这样可以抑制非极大值,保留局部梯度最大的点,以得到细化的边缘。
4、用双阈值算法检测和连接边缘
- 选取系数TH和TL,比率为2:1或3:1。(一般取TH=0.3或0.2,TL=0.1);
- 将小于低阈值的点抛弃,赋0;将大于高阈值的点立即标记(这些点为确定边缘点),赋1或255;
- 将小于高阈值,大于低阈值的点使用8连通区域确定(即:只有与TH像素连接时才会被接受,成为边缘点,赋 1或255)
代码实现
#include <iostream>
#include <opencv2/core.hpp>
#include <opencv2/highgui.hpp>
#include <opencv2/imgproc.hpp>
sobel算子/
//阶乘
int factorial(int n){
int fac = 1;
//0的阶乘
if (n == 0)
return fac;
for (int i = 1; i <= n; ++i){
fac *= i;
}
return fac;
}
//获得Sobel平滑算子
cv::Mat getSobelSmoooth(int wsize){
int n = wsize - 1;
cv::Mat SobelSmooothoper = cv::Mat::zeros(cv::Size(wsize, 1), CV_32FC1);
for (int k = 0; k <= n; k++){
float *pt = SobelSmooothoper.ptr<float>(0);
pt[k] = factorial(n) / (factorial(k)*factorial(n - k));
}
return SobelSmooothoper;
}
//获得Sobel差分算子
cv::Mat getSobeldiff(int wsize){
cv::Mat Sobeldiffoper = cv::Mat::zeros(cv::Size(wsize, 1), CV_32FC1);
cv::Mat SobelSmoooth = getSobelSmoooth(wsize - 1);
for (int k = 0; k < wsize; k++){
if (k == 0)
Sobeldiffoper.at<float>(0, k) = 1;
else if (k == wsize - 1)
Sobeldiffoper.at<float>(0, k) = -1;
else
Sobeldiffoper.at<float>(0, k) = SobelSmoooth.at<float>(0, k) - SobelSmoooth.at<float>(0, k - 1);
}
return Sobeldiffoper;
}
//卷积实现
void conv2D(cv::Mat& src, cv::Mat& dst, cv::Mat kernel, int ddepth, cv::Point anchor = cv::Point(-1, -1), int delta = 0, int borderType = cv::BORDER_DEFAULT){
cv::Mat kernelFlip;
cv::flip(kernel, kernelFlip, -1);
cv::filter2D(src, dst, ddepth, kernelFlip, anchor, delta, borderType);
}
//可分离卷积———先垂直方向卷积,后水平方向卷积
void sepConv2D_Y_X(cv::Mat& src, cv::Mat& dst, cv::Mat kernel_Y, cv::Mat kernel_X, int ddepth, cv::Point anchor = cv::Point(-1, -1), int delta = 0, int borderType = cv::BORDER_DEFAULT){
cv::Mat dst_kernel_Y;
conv2D(src, dst_kernel_Y, kernel_Y, ddepth, anchor, delta, borderType); //垂直方向卷积
conv2D(dst_kernel_Y, dst, kernel_X, ddepth, anchor, delta, borderType); //水平方向卷积
}
//可分离卷积———先水平方向卷积,后垂直方向卷积
void sepConv2D_X_Y(cv::Mat& src, cv::Mat& dst, cv::Mat kernel_X, cv::Mat kernel_Y, int ddepth, cv::Point anchor = cv::Point(-1, -1), int delta = 0, int borderType = cv::BORDER_DEFAULT){
cv::Mat dst_kernel_X;
conv2D(src, dst_kernel_X, kernel_X, ddepth, anchor, delta, borderType); //水平方向卷积
conv2D(dst_kernel_X, dst, kernel_Y, ddepth, anchor, delta, borderType); //垂直方向卷积
}
//Sobel算子边缘检测
//dst_X 垂直方向
//dst_Y 水平方向
void Sobel(cv::Mat& src, cv::Mat& dst_X, cv::Mat& dst_Y, cv::Mat& dst, int wsize, int ddepth, cv::Point anchor = cv::Point(-1, -1), int delta = 0, int borderType = cv::BORDER_DEFAULT){
cv::Mat SobelSmooothoper = getSobelSmoooth(wsize); //平滑系数
cv::Mat Sobeldiffoper = getSobeldiff(wsize); //差分系数
//可分离卷积———先垂直方向平滑,后水平方向差分——得到垂直边缘
sepConv2D_Y_X(src, dst_X, SobelSmooothoper.t(), Sobeldiffoper, ddepth);
//可分离卷积———先水平方向平滑,后垂直方向差分——得到水平边缘
sepConv2D_X_Y(src, dst_Y, SobelSmooothoper, Sobeldiffoper.t(), ddepth);
//边缘强度(近似)
dst = abs(dst_X) + abs(dst_Y);
cv::convertScaleAbs(dst, dst); //求绝对值并转为无符号8位图
}
//确定一个点的坐标是否在图像内
bool checkInRang(int r,int c, int rows, int cols){
if (r >= 0 && r < rows && c >= 0 && c < cols)
return true;
else
return false;
}
//从确定边缘点出发,延长边缘
void trace(cv::Mat &edgeMag_noMaxsup, cv::Mat &edge, float TL,int r,int c,int rows,int cols){
if (edge.at<uchar>(r, c) == 0){
edge.at<uchar>(r, c) = 255;
for (int i = -1; i <= 1; ++i){
for (int j = -1; j <= 1; ++j){
float mag = edgeMag_noMaxsup.at<float>(r + i, c + j);
if (checkInRang(r + i, c + j, rows, cols) && mag >= TL)
trace(edgeMag_noMaxsup, edge, TL, r + i, c + j, rows, cols);
}
}
}
}
//Canny边缘检测
void Edge_Canny(cv::Mat &src, cv::Mat &edge, float TL, float TH, int wsize=3, bool L2graydient = false){
int rows = src.rows;
int cols = src.cols;
//高斯滤波
cv::GaussianBlur(src,src,cv::Size(5,5),0.8);
//sobel算子
cv::Mat dx, dy, sobel_dst;
Sobel(src, dx, dy, sobel_dst, wsize, CV_32FC1);
//计算梯度幅值
cv::Mat edgeMag;
if (L2graydient)
cv::magnitude(dx, dy, edgeMag); //开平方
else
edgeMag = abs(dx) + abs(dy); //绝对值之和近似
//计算梯度方向 以及 非极大值抑制
cv::Mat edgeMag_noMaxsup = cv::Mat::zeros(rows, cols, CV_32FC1);
for (int r = 1; r < rows - 1; ++r){
for (int c = 1; c < cols - 1; ++c){
float x = dx.at<float>(r, c);
float y = dy.at<float>(r, c);
float angle = std::atan2f(y, x) / CV_PI * 180; //当前位置梯度方向
float mag = edgeMag.at<float>(r, c); //当前位置梯度幅值
//非极大值抑制
//垂直边缘--梯度方向为水平方向-3*3邻域内左右方向比较
if (abs(angle)<22.5 || abs(angle)>157.5){
float left = edgeMag.at<float>(r, c - 1);
float right = edgeMag.at<float>(r, c + 1);
if (mag >= left && mag >= right)
edgeMag_noMaxsup.at<float>(r, c) = mag;
}
//水平边缘--梯度方向为垂直方向-3*3邻域内上下方向比较
if ((angle>=67.5 && angle<=112.5 ) || (angle>=-112.5 && angle<=-67.5)){
float top = edgeMag.at<float>(r-1, c);
float down = edgeMag.at<float>(r+1, c);
if (mag >= top && mag >= down)
edgeMag_noMaxsup.at<float>(r, c) = mag;
}
//+45°边缘--梯度方向为其正交方向-3*3邻域内右上左下方向比较
if ((angle>112.5 && angle<=157.5) || (angle>-67.5 && angle<=-22.5)){
float right_top = edgeMag.at<float>(r - 1, c+1);
float left_down = edgeMag.at<float>(r + 1, c-1);
if (mag >= right_top && mag >= left_down)
edgeMag_noMaxsup.at<float>(r, c) = mag;
}
//+135°边缘--梯度方向为其正交方向-3*3邻域内右下左上方向比较
if ((angle >=22.5 && angle < 67.5) || (angle >= -157.5 && angle < -112.5)){
float left_top = edgeMag.at<float>(r - 1, c - 1);
float right_down = edgeMag.at<float>(r + 1, c + 1);
if (mag >= left_top && mag >= right_down)
edgeMag_noMaxsup.at<float>(r, c) = mag;
}
}
}
//双阈值处理及边缘连接
edge = cv::Mat::zeros(rows, cols, CV_8UC1);
for (int r = 1; r < rows - 1; ++r){
for (int c = 1; c < cols - 1; ++c){
float mag = edgeMag_noMaxsup.at<float>(r, c);
//大于高阈值,为确定边缘点
if (mag >= TH)
trace(edgeMag_noMaxsup, edge, TL, r, c, rows, cols);
else if (mag < TL)
edge.at<uchar>(r, c) = 0;
}
}
}
int main(){
cv::Mat src = cv::imread("I:\\Learning-and-Practice\\2019Change\\Image process algorithm\\Img\\lena.jpg");
if (src.empty()){
return -1;
}
if (src.channels() > 1) cv::cvtColor(src, src, CV_RGB2GRAY);
cv::Mat edge,dst;
//Canny
Edge_Canny(src, edge, 20,60);
//opencv自带Canny
cv::Canny(src, dst, 20, 80);
cv::namedWindow("src", CV_WINDOW_NORMAL);
imshow("src", src);
cv::namedWindow("My_canny", CV_WINDOW_NORMAL);
imshow("My_canny", edge);
cv::namedWindow("Opencv_canny", CV_WINDOW_NORMAL);
imshow("Opencv_canny", dst);
cv::waitKey(0);
return 0;
}效果
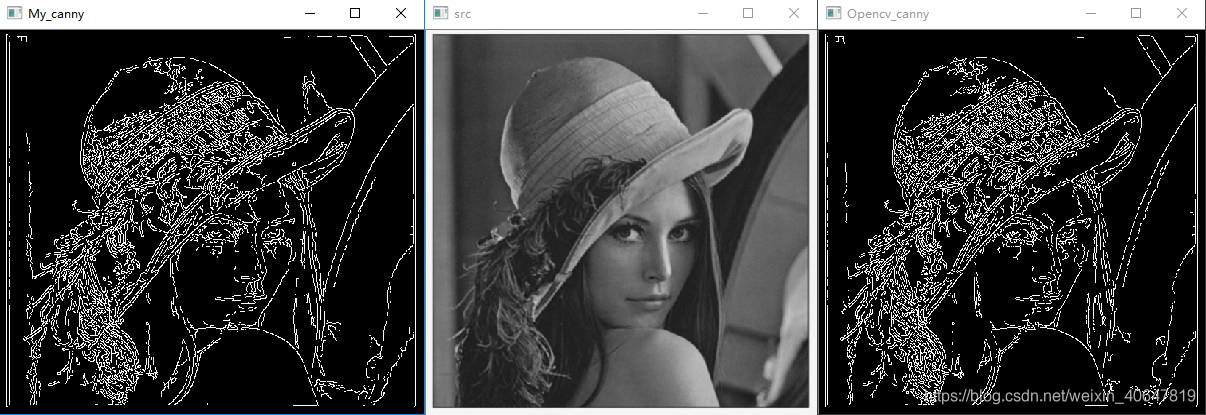
与OpenCV的Canny API做了对比。
opencv的canny API:
void Canny(InputArray image, OutputArray edges, double threshold1,
double threshold2, int apertureSize=3, bool L2gradient=false )
一些小注意点:
atan2返回给定的 X 及 Y 坐标值的反正切值。反正切的角度值等于 X 轴与通过原点和给定坐标点 (Y坐标, X坐标) 的直线之间的夹角。结果以弧度表示并介于 -pi 到 pi 之间(不包括 -pi)。 atan2(a, b) 与 atan(a/b)稍有不同,atan2(a,b)的取值范围介于 -pi 到 pi 之间(不包括 -pi), 而atan(a/b)的取值范围介于-pi/2到pi/2之间(不包括±pi/2)。
参考:
https://blog.csdn.net/weixin_40647819/article/list/2?
https://blog.csdn.net/liuzhuomei0911/article/details/51345591

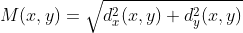
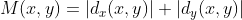

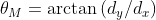
![\theta_{M}\in [0,22.5)\cup (-22.5,0]\cup (157.5,180]\cup (-180,157.5]](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvNzEyOTFhNTczMzYyYTQzODlhNDYzZGM3MWRhM2VkNmEuZ2lm)
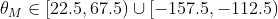
![\theta_{M}\in [67.5,112.5]\cup [-112.5,-67.5]](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvNTNjYjA0MjZmOTk2YzIzODg1MmM5NmQ0ZGVjODJmNzQuZ2lm)
![\theta_{M}\in (112.5,157.5]\cup [-67.5,-22.5]](/image/aHR0cHM6Ly9pLWJsb2cuY3NkbmltZy5jbi9ibG9nX21pZ3JhdGUvYmU0YzU3MjdjMjhmN2RhNTQ0MGFhYmQ3NGQyYTI4YjUuZ2lm)