2010年认证杯SPSSPRO杯数学建模
A题 聪明的汽车
原题再现:
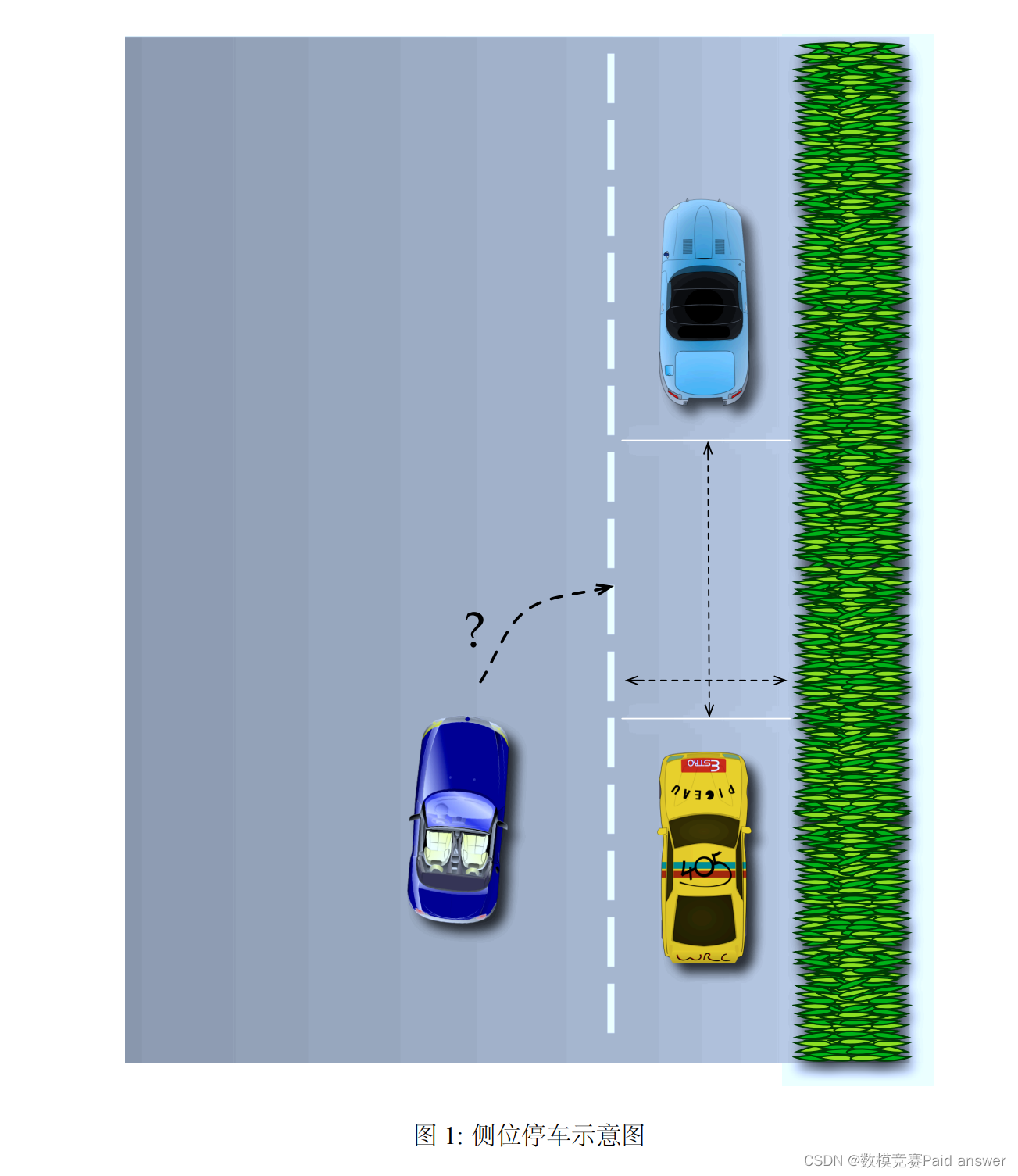
在狭窄的空间里把车停放在合适的位置,或在短小的停车位上侧位停车,一直是考验驾驶员技术与信心的问题。有调查报告称:57% 的驾驶员对自己的停车技术缺乏自信,这一方面影响人的驾驶体验,一方面也使停车空间不能得到充分利用。在此,请你协助驾驶员来解决停车的问题。具体要求如下:
第二阶段问题:
(1) 大型车辆有时也会面临在狭窄空间中停车的问题。例如铰接式的集装箱货车(见图2),车头和拖挂的集装箱拖车之间有可活动的连接部,所以整车在转弯时不是刚性的。对这样的车辆,请设计一个方法来判断本车是否能在保证安全的情况下停入侧向车位2。
(2) 通过第一阶段的工作,我们已经能够设计出较优的停车线路。但人工驾驶时操作可能不准确,由于客观条件3,也可能影响驾驶员的判断,使其不能按照设计的线路行进。假设我们可以实时测定本车的确切位置,请建立合理的模型,以根据本车的当前位置,随时提出建议的停车线路,并提出对驾驶员操作的建议。建议需要考虑实用性。为简化问题,在此问题中只需考虑小型车辆。
整体求解过程概述(摘要)
本论文主要是在第一阶段论文的基础上,研究铰接式的集装箱货车停车和实时改进停车路线,并将改进建议反馈给驾驶员。
第一问中铰接式的集装箱货车与第一阶段的小汽车相比,在转弯时是非刚性的。因此重新建立车体模型。 之后沿用第一阶段思路建立了轨迹判定模型, 重新确立约束条件。模型主要通过程序求解,输入车身参数,停车位置,转向角和停车位的长和宽来判定是否能进行停车。结果有计算机以自然语言的形式输出。在模型的改进中结合动态规划的思想,根据实际情况来调整转向角,达到合适的停车位置。
第二问解决了两个方面的问题。首先是运用动态规划的思想,将整个停车过程,看做多个状态,如果当前状态的下一个状态能进入较优路线,则进入下一个状态。如果不能则重新调整转向角。在转向角的所有范围内都不能满足要求时,就按原路返回至上一 个状态。对于状态转换建立了状态转换模型,判断下一状态是否能进入较优路线又建立了判定模型。其次,为提高驾驶员的实际操作体验,建立了驾驶员体验模型,主要将外侧轮转向角转换成实际的方向盘的圈数,并运用数据拟合对原先提出的线性正比模型进行了改进。模型的求解运用递归算法思想编程实现。
最后,对第一和第二问的模型分析了误差产生的原因和误差处理的思路方法。
问题分析
第(1)问与第一阶段的问题比较相似,但是由于铰接式的集装箱货车在转弯时非刚性。所以需要重新建立一个车体模型,来分析具体转弯的轨迹,在采用第一阶段判断小汽车是否可停车的方法来判断铰接式的集装箱货车是否可以停车
第(2)问需要解决两个方面的问题第一是小汽车沿较优路线行驶中,出现偏差后如何处理第二是提供给驾驶员的建议,要将小汽车的一些参数转换成驾驶员实际能够操作的参数(例如方向盘的圈数) 。
模型的假设:
1:汽车为 2 轮后轮驱动符合阿克曼转动特征公式
2:地面平整(无坡度和倾斜情况)
3:行驶过程中不出现侧滑,漂移等现象
4:车速对转角不产生影响。
5:汽车的最小转向半径是确定的。
6:最终停车位置为最佳位置(停车位正中间) 。
7:使用最短的合适的停车路线。
8:集装箱车分牵引车和挂车两部分,整车有牵引车的后轮驱动。
9:近似认为牵引车和挂车都符合阿克曼方程。
10:整个过程中车身保持匀速运动。
论文缩略图:
全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
部分程序代码:(代码和文档not free)
#include"stdio.h"
#include"math.h"
double pow(double a,int b)
{//求 b
a
int i;double temp=a;
for(i=0;i<b;i++)
{
temp=temp*a;
}
return temp;
}
int fun(double L , double L1 ,double S , double T , double W ,double Pw , double Pl,double
R1,double R2,double m,double n)
{//求
0 ) , (
0 ) , (
0 ) , (
3
2
1
£
£
£
l w
l w
l w
P P f
P P f
P P f
double f1=pow(R2+W,2)+pow(L1S,2)pow(R2+(Pw+W)/2,2);
double f2=pow((R2+W),2)pow(L1S,2)(pow(R2+(WPw)/2,2)+pow(PlL+T,2);
double f3=(pow(R1,2)pow(mR1,2)pow(LTn,2);
if(f2<=0&&f3<=0&&f4<=0)
return 1;
else
return 0;
}
main()
{//主函数
double L,L1,S,T,W,Pw,Pl,R1,R2,m,n;
scanf("%f,%f,%f,%f,%f,%f,%f,%f,%f,%f,%f",&L,&L1,&S,&T,&W,&Pw,&Pl,&R1,&R2,&m,
&n);
if(fun(L,L1,S,T,W,Pw,Pl,R1,R2,m,n)==1)
{
printf("可以停车\n");
}
else printf("不可以停车\n");
}
#include"stdio.h"
#include"math.h"
#define aMin 0.00;
#define aMax 3.14/4;
double m[3];
double n[3];
double a[3];
int fun(double m, double n,double a)
{
double temp ;
int flag=0;
temp =m/2+(L+S)*(L+S)/(2*m)+WL/tan(a);//L,S,W 为已知常数
if(temp<=0)
flag 1;
return flag;
}
double search(double a)
{
double temp=aMin+(aMaxaMin)*100/random(100);
if(temp!=a)
temp=temp;
else temp=+1/100;
return temp;
}
double convert(double a)
{
return k*a/7.28;//k 为常数
}
State(double m, double n,double a)
{
if(a<=aMax&&a>=aMin)
{
if(fun(m,n,a)==1)
m[2]=m[1](r1abs(r1cos(theta)sqr((r2+W+r1)*(r2+W+r1)n[1]*n[1])))
n[2]=n[1]+abs(n[1]r1sin(theta))
a[2]=a[1];//r1,theta,r2,W,为可测到的常数
}
else
{
m[2]=m[1];
n[2]=n[1];
a[2]=search(a[1]);
printf("方向有误,请调整方向盘%f 圈",convert(a[2])conver(a[1]));
}
}
else
{
m[2]=m[0];
n[2]=n[0];
a[2]=a[0];
printf("请按原始路线返回,方向盘转%f 圈!",convert( a[0]));
}
State( m[2], double n[2],double a[2])