”变基“操作(即换个坐标系,或旋转坐标系),使得这组数据在我们的新坐标系下,其协方差矩阵为对角矩阵。在方差较大的维度上,数据是较为分散的,保留了原始数据的大部分信息。而在方差较小的维度上,数据几乎没有波动,这些维度我们完全可以丢掉。因此可以起到降维的效果。(当我们的新基相对与旧基只是一个旋转变换的时候,各样本点到样本均值之间的距离是不变的。这个距离的均值等于协方差矩阵的迹,也即各个维度内部的方差之和。因此一些维度方差最大,另一些维度必然方差最小)。
PCA、协方差矩阵以及在点云处理中的应用_点云协方差矩阵-CSDN博客
基础知识:
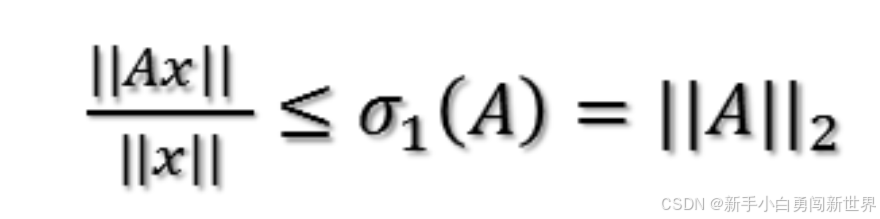
为A最大奇异值。
核心思想:
1、给定一组数据Z={z1,z2,z3,z4......zn}; z是一个列向量,每个z代表一个特征,求出每个特征的均值 后中心数据,即每个特征向量减去他的均值得到X。
2、寻找可以让X分布散的最开的方向d1,也就是说X在d1方向上的投影的绝对值之和最大。投影的方法就是将X与d1做内积。即最大化,
证明参考:PCA(主成分分析)-------原理,推导,步骤、实例、代码_pca一般步骤-CSDN博客
3、故d1的方向为XX'最大特征值方向
步骤:
1.我们一般选择一行是一个特征,对每个特征求平均值;原来的数据减去平均值得到新的中心化之后的数据;
2.求特征协方差矩阵;
3.根据协方差矩阵,求特征值与特征向量
4.对特征值按照降序的顺序排列,相应的也给出特征向量,选择几个主成分,求投影矩阵(选定的几个特征值对应的特征向量)。
5.根据投影矩阵求出我们降维后的数据。
结论:
1.降维是一种数据集预处理技术,往往在数据应用其他算法之前使用,它可以去除数据的一些冗余信息和噪声。
2.PCA可以从数据中识别主要特征,通过将数据坐标轴旋转到数据角度上那些最重要的方向(方差最大),然后通过特征值分析,确定出需要保留的主成分个数,舍弃其他主成分,从而实现数据的降维。
在点云中应用:
1、边缘检测:位于边缘处的点云从线性变换的角度看,就是存在一个维度,点云拉伸的程度很大,另外两个维度则比较小。因此点云协方差矩阵的特征值可以反映一个点是否是边缘点。计算特征值,判断是否超过阈值,决定是否为边缘点。
2、法向量计算:再想象一组呈平面分布的点云,我们想求其法向量,那实际上是找到新的基向量
,使得点云在新的基向量方向上最为分散,在其中一个方向上最集中。
3、点云的Oriented Bounding Box(方向包围盒) 的计算,可以使用PCA计算出OBB的主轴。
4、点云的粗配准,可以使用PCA得到位姿的初始估计。