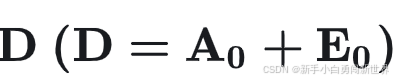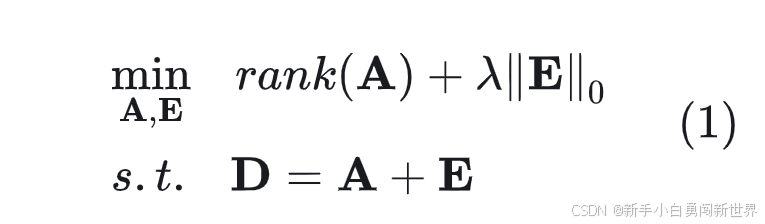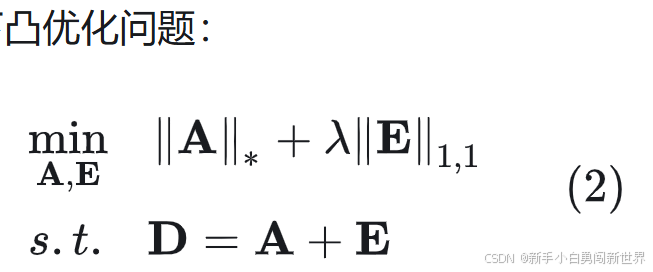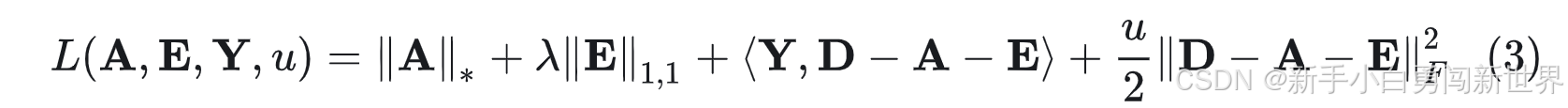将矩阵分解为低秩矩阵和独立同分布的高斯矩阵是PCA

当矩阵 E0 为稀疏的噪声矩阵时，分解为一个低秩矩阵部分 A 和一个稀疏矩阵部分 E 的

矩阵的秩和 ℓ0 范数问题都可以进行凸松弛，矩阵的核范数是矩阵秩的凸包络，（1）变成凸优化问题

解算方法;

1. 迭代阈值算法 对于PCP问题时，迭代阈值算法(Iterative Thresholding, IT) 通过交替更新矩阵 A 和 E 来求解。IT算法的迭代形式简单且收敛，但它的收敛速度比较慢，且难以选取合适的步长。因此，IT算法具有有限的应用范围。
2. 加速近端梯度算法 加速近端梯度算法(Accelerated Proximal Gradient, APG)的主要思想是利用了Nesterov加速，使算法能够快速收敛。
3. 对偶方法 将原问题转化为其对偶问题(非线性、非光滑)，并使用最速上升法等可以求解。对偶方法比APG算法具有更好的可扩展性，这是因为在每次迭代过程中对偶方法不需要矩阵的完全奇异值分解。
4. 增广拉格朗日乘子法即交替方向方法(Alternating direction methods, ADM)，也称为不精确拉格朗日乘子法(Inexact ALM, IALM)。

2. 交替方向算法(ADM)

对于优化问题(2)，首先构造增广拉格朗日函数：