文章介绍Apriltag的编解码系统,参考文献: AprilTag: A robust and flexible visual fiducial system
Edwin Olson
University of Michigan
[email protected]
http://april.eecs.umich.edu
编解码概述
当数据负载从方形中找到的时候,接下来就需要编码系统来判定他是否是可行的,设计编码系统的目标是:
·最大化可区分编码数量
·最大化可以检测和纠正的位错误数量
·最小化误报和标签间混淆的概率
·最小化标签的总位数和标签的大小
这些目标之间经常是会冲突的,所以一套给定的标签编码代表了一种妥协和权衡。这里我们描述一种基于词典的新标签编码系统,他和以往的编码方法相比有着显著的优势。我们的程序可以生成具有各种属性的词典,让用户能够挑选出最适合他们的需要的标签编码系统进行使用。
算法
我们建议使用修改过的词典系统。传统的词典是使用(每一个编码的位数n和两个标签之间的最小汉明距离d)两个量来参数化的。词典编码可以纠正(d-1)/2位的比特错误,并且能够检测d/2的比特错误。为了方便起见,我们会展示36h10编码族,他使用36位进行编码并且最小汉明距离是10。
词典码从用于生成有效码字的过程中得到名称的:候选码以字典顺序(从最小到最大)被考虑,当他们和之前添加到码本的每一个码字的至少距离都是d的时候,将新码字添加到码本,虽然非常的简单,但是这种方案通常会非常的接近最优。
再视觉基准的情况下,编码方法必须对旋转是鲁棒的。换句话说,当标签旋转90,180,270的时候,标签码字之间依然保持d的最小汉明距离。标准的词典生成算法不保证这个属性,但是可以通过简单的扩展来保证这个属性:当测试新的候选码字的时候,我们可以简单的确保所有四个旋转都具有所需要的最小汉明距离。词典算法能够很容易被扩展到包含额外的约束这是我们的编码方式的一个优点。
有一些码字尽管满足汉明距离的约束,但是依然是糟糕的选择。例如,全0码字会导致标签看起来就像是单个黑色的方块,这种简单的几何图形通常会出现在自然场景中,从而导致误报的发生。例如,ARTag就明确禁止两个编码,因为他们很可能会偶然发生。
我们不是手动识别有问题的标签,而是通过拒绝导致简单几何图行的候选码自来进一步修改词典生成算法。我们的度量基准是基于生成标签2D图案所需要的矩形数量。比如,一个实心的标签只需要一个矩形,而黑白条纹需要两个矩形。我们的假设,在本文后面的实验结果支持下具有高复杂性的标签模式(需要很多的矩形来组成),在自然条件下发生的频率极低,因此可以有较低的假阳性率。
通过这个想法,我们再次修改词典生成算法来拒绝过于简单的候选码字。我们使用简单的贪婪算法来近似生成标签模式所需要的矩形的数量,这个方法重复考虑所有可能的矩形并且添加最能够减少错误的矩形。由于标签通常非常的小,所以计算量不是一个瓶颈。最小复杂度小于阈值的标签(实验中设置为10)被我们舍弃掉。结果部分演示了这种构造方式的适当性和有效性。
最后,我们通过对词典生成算法进行一次修改,观察到了比较低的误报率。我们不考虑按顺序(0,1,2,3,4,5,6,7.。。)的测试码字,而是考虑(b,b+1p,b+2p,b+3p…)其中b是任意的数,p是一个大的素数,每一步都保留最低的n位。直觉上,这种方法生成的标签在每一个比特位置都有更大的熵,同时词典顺序有利于小值码字。这种方式的缺点是创建出来的码字的数量可能会更少一些:词典排序能够更加密集的打包码字,而更随机的顺序导致码字的打包效率更低一些。
总的来说,我们使用字典码字生成系统可以生成任意大小的标签(33,44,55,66等)和最小汉明距离的码字。我们的方法明确保证每一个标签的所有四个旋转的最小汉明距离,并且消除几何复杂度低的标签,计算标签可能是一项昂贵的操作,但是可能离线完成,小标签可以在几秒或者几分钟内轻松的计算完成,但是大的(6*6)标签可能需要几天的CPU时间。许多有用的编码族我们已经计分配算好了;大多数用户不需要生成自己的编码族。
纠错分析
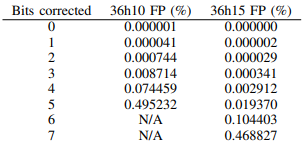
可以容易的分析理论上的假阳性率。假设识别出错误的四边形并且位模式是随机的,误报的概率就是被接受为有效标签的码字数量和所有可能的码字的总数的比值。更加积极的纠错会增加这个速率,因为他会增加被接受的码字的数量。下面的36h10和36h15码字说明了这种不可避免的错误率的增加。
当然,36h15编码拥有更好的性能是有代价的:只有27个可以区分的码字,而不是36h10的2221个可以区分的码字。
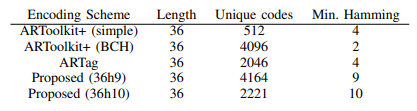
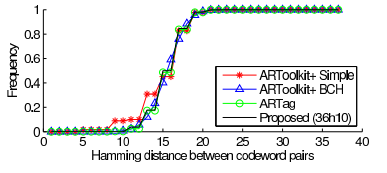
我们的编码方案明显强于之前的方案,包括ARTag和ARToolkitPlus使用的两种方案:我们的编码系统在完成编码比较多的码字的同时能够达到一个更大的最小汉明距离。最小汉明距离的改善如图和下表所示:
(汉明距离,好的编码在有效码字之间具有更大的汉明距离,上面显示的是几个现有系统的汉明距离。注意,我们的编码方案通过构造来保证最小汉明距离,而其他的系统具有一些很相似的码字,这会导致更高的标签间混淆的概率。)
为了解码可能被损坏的码字,我们需要计算码字和编码词典之间的汉明距离。如果最佳匹配的汉明距离小于用户设定的阈值,那么就报告一次检测。通过指定特定的阈值,用户能够在假真和假假之间进行权衡选择。
这个方法的一个缺点就是这个解码过程花费了码字词典大小的线性时间,因为在这个过程当中,必须要考虑每一个有效的码字,不过,这个系数非常的小,以至于和其他的图像处理步骤相比这个耗时可以忽略不记。
对于给定的标签编码方案,更大的标签(例如36bits和25bits)编码性能会明显优于较小的标签,当然这是需要付出代价的。在其他条件相同情况下,给定摄像机读取36位标签的范围将短于同一个摄像机读取16位或者25位的标签的范围。然而由于标签的四像素开销,比较小的标签的范围的好处非常使用,使用16位标签而不是36位标签,可以预期检测范围仅提高25%。因此,仅在较大的范围敏感的应用中,比较小的标签是有利的。