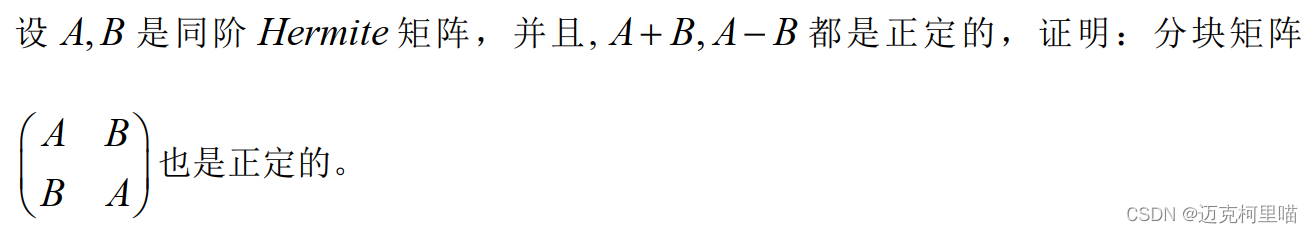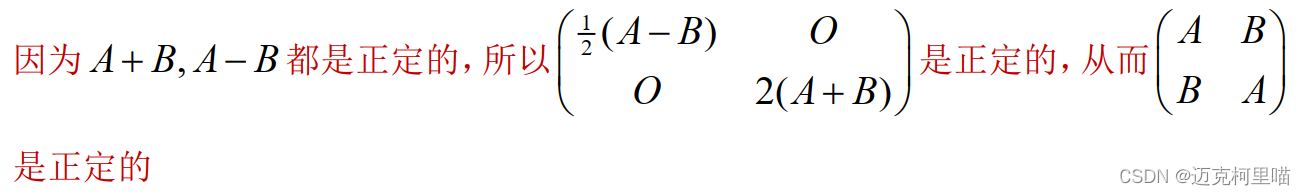一、用「初等变换法」求实对称矩阵所合同的对角阵
为了使本文完整,这里先阐述一下如何使用「初等变换法」求实对称矩阵所合同的对角阵。
在学习线性代数时,我们知道,对于任意一个 n × n n \times n n×n 的实对称矩阵 A A A,可以使用「初等变换法」,求出可逆矩阵 C C C 及对角矩阵 D D D,使得 A A A 与 D D D 合同,即 C T A C = D C^TAC=D CTAC=D,其中 C T C^T CT 表示 C C C 的转置。
具体做法:作 2 n × n 2n \times n 2n×n 矩阵
[ A I ] → 对 2 n × n 矩阵施行相同的初等列变换 对 A 施行初等行变换 [ D C ] \left[ \begin{matrix} A\\ I \end{matrix} \right] \xrightarrow[对2n\times n矩阵施行相同的初等列变换]{对A施行初等行变换} \left[ \begin{matrix} D\\ C \end{matrix} \right] [AI]对A施行初等行变换对2n×n矩阵施行相同的初等列变换[DC]
则 C T A C = D C^TAC=D CTAC=D。
注意,需要先施行初等行变换,然后立即对整个列施行相同的初等列变换。
例 1
已知实对称矩阵
A
=
[
1
1
1
1
2
3
1
3
5
]
A= \left[ \begin{matrix} 1 & 1 & 1\\ 1 & 2 & 3\\ 1 & 3 & 5\\ \end{matrix} \right]
A=
111123135
用初等变换法求可逆矩阵
C
C
C 及对角阵
D
D
D,使得
A
A
A 与
D
D
D 合同。
[
A
I
]
=
[
1
1
1
1
2
3
1
3
5
1
0
0
0
1
0
0
0
1
]
→
c
2
−
c
1
r
2
−
r
1
[
1
0
1
0
1
2
1
2
5
1
−
1
0
0
1
0
0
0
1
]
→
c
3
−
c
1
r
3
−
r
1
[
1
0
0
0
1
2
0
2
4
1
−
1
−
1
0
1
0
0
0
1
]
→
c
3
−
c
2
r
3
−
r
2
[
1
0
0
0
1
0
0
0
0
1
−
1
1
0
1
−
2
0
0
1
]
\left[ \begin{matrix} A\\ I \end{matrix} \right]= \left[ \begin{matrix} 1 & 1 & 1\\ 1 & 2 & 3\\ 1 & 3 & 5\\ 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{matrix} \right] \xrightarrow[c_2-c_1]{r_2-r_1} \left[ \begin{matrix} 1 & 0 & 1\\ 0 & 1 & 2\\ 1 & 2 & 5\\ 1 & -1 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{matrix} \right] \xrightarrow[c_3-c_1]{r_3-r_1} \left[ \begin{matrix} 1 & 0 & 0\\ 0 & 1 & 2\\ 0 & 2 & 4\\ 1 & -1 & -1\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{matrix} \right] \xrightarrow[c_3-c_2]{r_3-r_2} \left[ \begin{matrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 0\\ 1 & -1 & 1\\ 0 & 1 & -2\\ 0 & 0 & 1\\ \end{matrix} \right]
[AI]=
111100123010135001
r2−r1c2−c1
101100012−110125001
r3−r1c3−c1
100100012−110024−101
r3−r2c3−c2
100100010−1100001−21
所求可逆矩阵
C
C
C 及对角阵
D
D
D 分别为
C
=
[
1
−
1
1
0
1
−
2
0
0
1
]
,
D
=
[
1
0
0
0
1
0
0
0
0
]
C= \left[ \begin{matrix} 1 & -1 & 1\\ 0 & 1 & -2\\ 0 & 0 & 1\\ \end{matrix} \right], D= \left[ \begin{matrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 0\\ \end{matrix} \right]
C=
100−1101−21
,D=
100010000
且 C T A C = D C^TAC=D CTAC=D。
二、用「初等变换法」求分块对称阵所合同的分块对角阵
下面,我们将实对称矩阵,拓展到分块对称阵,矩阵内的元素也不再局限于实数,可以是复数。我们不加证明地通过类比上面的初等变换法,给出求分块对称阵所合同的分块对角阵的初等变换法。
对于一个 n × n n \times n n×n 的分块对称阵 A A A,可以使用「初等变换法」,求出可逆矩阵 C C C 及分块对角矩阵 D D D,使得 A A A 与 D D D 合同,即 C H A C = D C^HAC=D CHAC=D,其中 C H C^H CH 表示 C C C 的共轭转置。
具体做法:作
2
n
×
n
2n \times n
2n×n 的矩阵
[
A
I
]
→
对
2
n
×
n
矩阵施行相同的初等列变换
对
A
施行初等行变换
[
D
C
]
\left[ \begin{matrix} A\\ I \end{matrix} \right] \xrightarrow[对2n\times n矩阵施行相同的初等列变换]{对A施行初等行变换} \left[ \begin{matrix} D\\ C \end{matrix} \right]
[AI]对A施行初等行变换对2n×n矩阵施行相同的初等列变换[DC]
则
C
H
A
C
=
D
C^HAC=D
CHAC=D。
另外,还需要了解分块矩阵的初等变换法则,如下:
-
分块矩阵的初等行变换规则
- 把一个块行的左 P P P 倍( P P P 是矩阵)加到另一个块行上;
- 交换两个块行的位置
- 用一个可逆矩阵左乘某一块行
-
分块矩阵的初等列变换规则
- 把一个块列的右 P P P 倍( P P P 是矩阵)加到另一个块列上;
- 交换两个块列的位置
- 用一个可逆矩阵右乘某一块列
-
需要注意行变换和列变换时,有「左」和「右」的区别。
-
而且(重点),对如果把一个块行的左 P P P 倍( P P P 是矩阵)加到另一个块行上,其对应的相同的初等列变换是,把对应块列的右 P H P^H PH(注意这里有个共轭转置) 倍加到另一个块列上。
直接看下面的例子会比较容易理解。
例2
已知分块对角阵
B
=
[
A
α
α
H
1
λ
0
]
B= \left[ \begin{matrix} A & \alpha\\ \alpha^H & \frac{1}{\lambda_0} \end{matrix} \right]
B=[AαHαλ01]
其中
A
A
A 是
n
×
n
n \times n
n×n 的 Hermite 阵(即
A
H
=
A
A^H=A
AH=A),且
A
A
A 正定,
α
\alpha
α 是
n
n
n 维单位列向量。用初等变换法求可逆矩阵
C
C
C 及对角阵
D
D
D,使得
B
B
B 与
D
D
D 合同。
[ B I ] = [ A α α H 1 λ 0 I n O O 1 ] → c 2 − c 1 ( α H A − 1 ) H r 2 − α H A − 1 r 1 [ A O O 1 λ 0 − α H A − 1 α I n − ( A H ) − 1 α O 1 ] \left[ \begin{matrix} B\\ I\\ \end{matrix} \right]= \left[ \begin{matrix} A & \alpha\\ \alpha^H & \frac{1}{\lambda_0}\\ I_n & O\\ O & 1 \end{matrix} \right] \xrightarrow[c_2-c_1(\alpha^HA^{-1})^H]{r_2-\alpha^HA^{-1}r_1} \left[ \begin{matrix} A & O\\ O & \frac{1}{\lambda_0}-\alpha^HA^{-1}\alpha\\ I_n & -(A^H)^{-1}\alpha\\ O & 1 \end{matrix} \right] [BI]= AαHInOαλ01O1 r2−αHA−1r1c2−c1(αHA−1)H AOInOOλ01−αHA−1α−(AH)−1α1
所求可逆矩阵 C C C 及对角阵 D D D 分别为
C
=
[
I
n
−
(
A
H
)
−
1
α
O
1
]
,
D
=
[
A
O
O
1
λ
0
−
α
H
A
−
1
α
]
C= \left[ \begin{matrix} I_n & -(A^H)^{-1}\alpha\\ O & 1 \end{matrix} \right], D= \left[ \begin{matrix} A & O\\ O & \frac{1}{\lambda_0}-\alpha^HA^{-1}\alpha\\ \end{matrix} \right]
C=[InO−(AH)−1α1],D=[AOOλ01−αHA−1α]
且
C
H
A
C
=
D
C^HAC=D
CHAC=D。
需要注意的是,因为 B B B 是分块矩阵,所以单位阵 I I I 也得分块,而且分块方式要和 B B B 一致。
三、应用-判断矩阵的正定性
看一道工程矩阵(也可能出自高等代数)的题目:
求一个分块对角阵,与原分块对称阵合同, 常用于分析一个分块矩阵的正定性,例如下面这题。
答案:
上面这道题的答案里用
E
E
E 表示单位阵,前文中用的是
I
I
I 需要注意一下。
这道题里的第一步求出与原矩阵共轭合同的矩阵,就是用到了本文的方法。
另外,两个矩阵如果共轭合同,它们的正定性将保持一致,所以可以通过初等变换,求出一个与原矩阵共轭合同的新矩阵,而且这个新矩阵的正定性很容易证明,那么原矩阵的正定性就随之证明出来了。