论文名称：Interdependence-Adaptive Mutual Information Maximization for Graph Contrastive Learning
论文地址：https://ieeexplore.ieee.org/document/10596072/
论文来源：IEEE Trans. Knowl. Data Eng. 2024
论文作者：Qingqiang Sun, Kai Wang, Wenjie Zhang, Peng Cheng, Xuemin Lin
代码地址：https://github.com/sunisfighting/IDEAL

1.问题引入

1.增强不变性（Augmentation-invariant）：仅选择来自同一节点的不同视图的表示作为正样本，忽略了不同节点之间的语义信息。
2.基于分布的相互依赖：需要额外的分布挖掘技术（如图聚类、kNN搜索和混合模型拟合）来提取正样本，这增加了计算负担，并且其效果高度依赖于预先学习的嵌入空间的质量。
3.基于结构的相互依赖：基于同质性假设（即连接的节点应该是相似的），将两个节点的表示视为正样本。然而，这种假设在不同数据集或领域中的可信度不同，且图增强进一步复杂化了节点间的关系。

2.本文贡献

1.重新定义跨视图依赖：创新性地从信息流的角度定义跨视图相互依赖，并据此提出了具有相互依赖自适应对比目标的自监督节点表示学习的IDEAL框架。
2.理论分析：证明了IDEAL的目标函数同时利用了对比学习和生成学习的优势，分析揭示了三元一致性学习（Tripartite Agreement Learning）效应是相互依赖-适应机制的结果。
3.实验验证：通过在多个具有不同规模和属性的基准数据集上的广泛实验，证明了IDEAL在自监督方法中始终优于现有的最先进方法，并且在训练效率上也有显著提升。

3.方法详解

3.1 信息流角度解读跨试图相互依赖

3.1.1 基本公式

• SSL获取节点表示
  SSL的目标是在不使用任何外部监督信号的情况下学习一个编码器f$f_{\theta }:{\mathbb{R}}^{N\times F}\times {\mathbb{R}}^{N\times N}\to {\mathbb{R}}^{N\times D}$，使得高层表示$f_{\theta }(\mathcal{G})=f_{\theta }(\mathbf{X},\mathbf{A})=\mathbf{Z}$可以用于下游任务，其中$\theta$为编码器的参数，$F$为特征维度数，$D$为学习到的节点表示的维数。
• 基于增强的对比范式
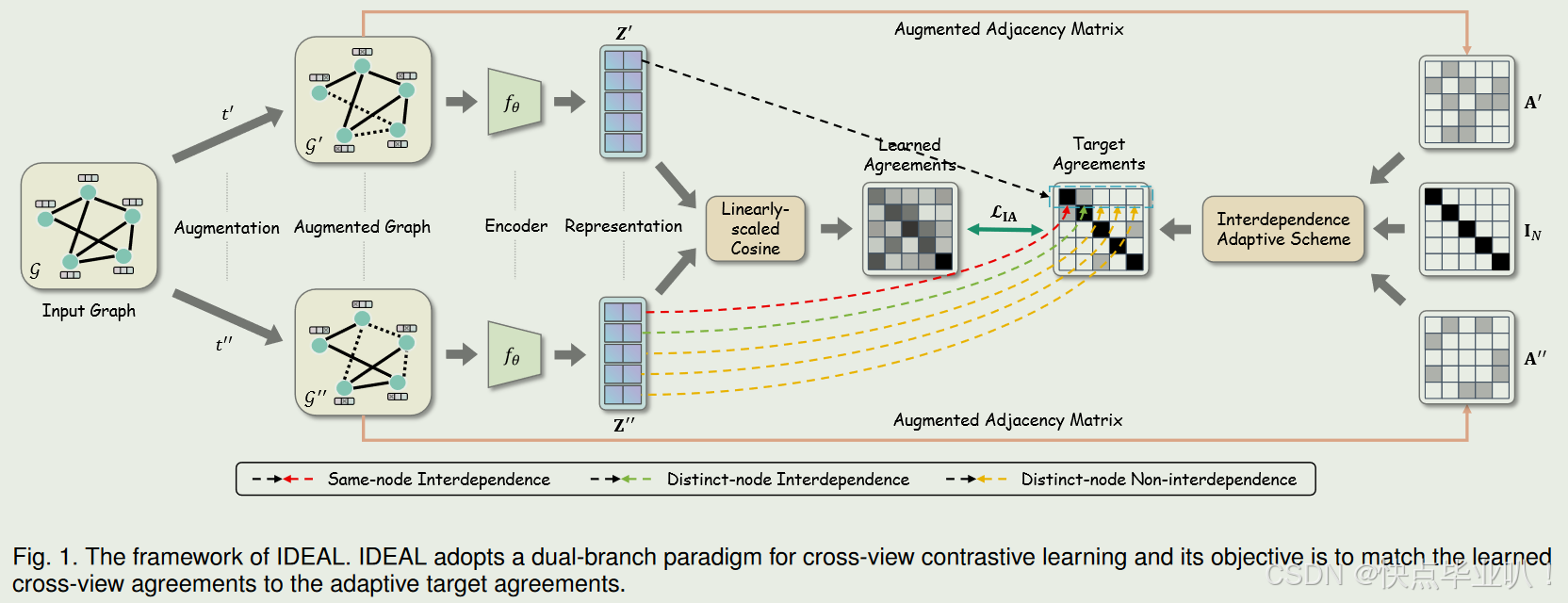
  本文采用的是组合增强的双分支范式，即每个增强视图都是通过特征掩码和边丢弃改变图结构。具体地，由原始图$\mathcal{G}=(\mathcal{V},\mathcal{E})$生成两个具有相同超参数的增强视图，即${\mathcal{G}}^{\prime }=({\mathbf{X}}^{\prime },{\mathbf{A}}^{\prime })=t(\mathcal{G};p_f,p_e)$和${\mathcal{G}}^{\prime \prime }=({\mathbf{X}}^{\prime \prime },{\mathbf{A}}^{\prime \prime })=t(\mathcal{G};p_f,p_e)$。其中，$p_f$和$p_e$分别表示特征掩码的一个维度和边丢弃的概率。由于增强的随机性，${\mathcal{G}}^{\prime }\ne {\mathcal{G}}^{\prime \prime }$几乎总是成立。

3.1.2 信息流相关解释

• 基于信息流的相互依赖
  对于图中任意节点$v_i$，$v_j$，当且仅当 ${\mathrm{z}}_j=\Omega ({\mathrm{x}}_i)$和 ${\mathrm{z}}_i=\Omega ({\mathrm{x}}_j)$时（即${\mathrm{x}}_i\to {\mathrm{z}}_j$与${\mathrm{x}}_j\to {\mathrm{z}}_i$同时存在），学习到的节点表示$z_i$，$z_j$是相互依赖的。
• 基于特征增强的信息流
  ${\mathrm{x}}_i^{\prime }=t_f^{\prime }({\mathrm{x}}_i)$
  ${\mathrm{x}}_i^{\prime \prime }=t_f^{\prime \prime }({\mathrm{x}}_i)$
  其中， $t_f^{\prime }:{\mathbb{R}}^F\to {\mathbb{R}}^F$ 和 $t_f^{\prime \prime }:{\mathbb{R}}^F\to {\mathbb{R}}^F$是特定的特征增强函数。${\mathrm{x}}_i$表示原始图中节点 𝑖 的特征，${\mathrm{x}}_i^{\prime }$和${\mathrm{x}}_i^{\prime \prime }$分别是第一个和第二个增强视图中节点 𝑖 的特征，信息流表示为 ${\mathrm{x}}_i\to {\mathrm{x}}_i^{\prime }$和 ${\mathrm{x}}_i\to {\mathrm{x}}_i^{\prime \prime }$。
• 基于卷积编码的信息流
  ${\mathrm{z}}_i^{\prime }=g({\mathrm{X}}_i^{\prime })$
  其中， X i ′ = { x j ′ ∣ j ∈ N ′ ( i ) ∩ { i } } \mathrm{X}_i' = \{\mathrm{x}_j' | j \in \mathcal{N}'(i) \cap \{i\}\} Xi′​={xj′​∣j∈N′(i)∩{i}}是第一个增强视图中节点 𝑖 的邻接节点特征集合，${\mathcal{N}}^{\prime }(i)$是由图卷积算子和边丢弃增强指定的节点 𝑖 的邻域， g : R F × ∣ N ′ ( i ) ∩ { i } ∣ → R F g : \mathbb{R}^{F\times|\mathcal{N}^{\prime}(i)\cap\{i\}|} \to \mathbb{R}^F g:RF×∣N′(i)∩{i}∣→RF 是图卷积编码函数，它将输入特征集合 ${\mathrm{X}}_i^{\prime }$ 映射到输出表示 ${\mathrm{z}}_i^{\prime }$。对于集合 ${\mathrm{X}}_i^{\prime }$ 中的每个 ${\mathrm{x}}_j^{\prime }$，存在从 ${\mathrm{x}}_j^{\prime }$ 到 ${\mathrm{z}}_i^{\prime }$ 的信息流，即存在 $\forall {\mathrm{x}}_j^{\prime }\in {\mathrm{X}}_i^{\prime },{\mathrm{x}}_j^{\prime }\to {\mathrm{z}}_i^{\prime }$。
• Remark
  节点特征掩码增强直接导致信息从原始视图流向节点的增强视图。虽然边丢弃的增强不会引起信息流，但它隐式地对基于卷积编码的信息流产生影响，因为局部邻域会随着边的丢弃而被修改。由于来自较远邻居的信息需要经过更长的路径才能到达目标节点，因此本文只考虑来自一跳邻居的直接信息流，即 N ′ ( i ) = { j ∣ ( v i ′ , v j ′ ) ∈ E ′ } \mathcal{N'}(i)=\{j\mid(v_{\boldsymbol{i}}',v_{\boldsymbol{j}}')\in\mathcal{E'}\} N′(i)={j∣(vi′​,vj′​)∈E′}。

3.1.3 跨视图相互依赖

本文从两个互补的视角来考察跨视图相互依赖，即同节点相互依赖和不同节点相互依赖。

• 同节点相互依赖
  作为从同一个节点$v_i$扩展而来的视图的学习表示，${\mathrm{z}}_i^{\prime }$和${\mathrm{z}}_i^{\prime \prime }$是相互依赖的。
• 不同节点相互依赖
  当且仅当$(v_i^{\prime },v_j^{\prime })\in {\mathcal{E}}^{\prime }$和$(v_i^{\prime \prime },v_j^{\prime \prime })\in {\mathcal{E}}^{\prime \prime }$同时成立时，节点表示${\mathrm{z}}_i^{\prime }$和${\mathrm{z}}_i^{\prime \prime }$相互依赖。其中，${\mathcal{E}}^{\prime }$和${\mathcal{E}}^{\prime \prime }$是两个增强视图的边集。
  
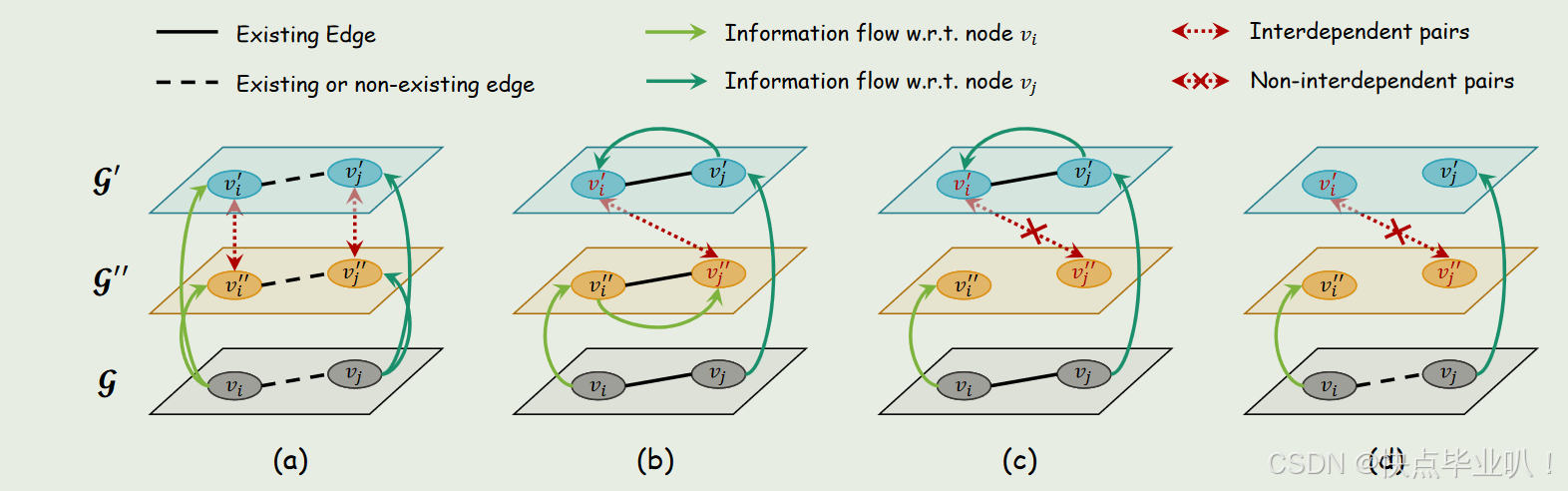
  图a：无论节点之间是否存在边，$v_i^{\prime }$和$v_i^{\prime \prime }$均来自原始图中的节点$v_i$，同理，$v_j^{\prime }$和$v_j^{\prime \prime }$也均来自原始图中的节点$v_j$，因此两增强视图学习得到的节点表示是互相依赖的（同节点相互依赖）。
  图b：对于来自增强视图中不同节点$v_i^{\prime }$和$v_j^{\prime \prime }$，由于满足条件$(v_i^{\prime },v_j^{\prime })\in {\mathcal{E}}^{\prime }$和$(v_i^{\prime \prime },v_j^{\prime \prime })\in {\mathcal{E}}^{\prime \prime }$同时成立，信息流是可以在二者之间传递的，故节点$v_i^{\prime }$和$v_j^{\prime \prime }$是相互依赖的。
  图c和图d：不满足$(v_i^{\prime },v_j^{\prime })\in {\mathcal{E}}^{\prime }$和$(v_i^{\prime \prime },v_j^{\prime \prime })\in {\mathcal{E}}^{\prime \prime }$同时成立，图c只有一个视图有边，图d两视图都没有边，故节点$v_i^{\prime }$和$v_j^{\prime \prime }$没有相互依赖关系，信息流无法传递。

3.2 IDEAL模型

• 目标一致性矩阵
  通过跨视图相互依赖关系的解释，我们可以直观看出，相互依赖的表征对包含了一定程度的关于对方的信息，因此应该将它们视为正对，在对比时应将它们拉在一起。
  因此，基于增强视图的结构，本文设置了一个目标一致性矩阵 S ∈ { 0 , 1 } N × N \mathbf{S}\in\{0,1\}^{N\times N} S∈{0,1}N×N。其中行和列索引分别表示第一和第二增广视图中的表征。具体地，若${\mathbf{z}}_i^{\prime }$与${\mathbf{z}}_j^{\prime \prime }$相互依赖，则$S_{ij}=1$；否则，$S_{ij}=0$。具体计算方式如下：
  $${\mathbf{S}}_{\mathrm{same}}={\mathbf{I}}_N,{\mathbf{S}}_{\mathrm{dist}}={\mathbf{A}}^{\prime }\odot {\mathbf{A}}^{\prime \prime },\mathbf{S}={\mathbf{S}}_{\mathrm{same}}+{\mathbf{S}}_{\mathrm{dist}}$$
  其中⊙表示Hadamard积，${\mathbf{S}}_{\mathrm{same}}$，${\mathbf{S}}_{\mathrm{dist}}$，$\mathbf{S}$是分别是关于相同节点，不同节点和完全跨视图相互依赖的目标一致性矩阵。
• 学习一致性矩阵
  学习一致性矩阵是通过模型在学习过程中得到的，反映模型当前学习到的节点表示之间的相似性或一致性。由模型框架可以看出，每个增强视图都是通过特征掩码和边丢弃生成的，然后送入GCN编码器学习到两视图的节点表示${\mathbf{Z}}^{\prime }$和${\mathbf{Z}}^{\prime \prime }$。
  大多数工作在内积或双线性函数之前引入一个额外的多层感知器( MLP )作为参数投影头，通常将其视为判别器的额外组件。本文采用了一个常用于文本相似度的线性缩放余弦( Linearly-Scaled Cosine，LSC )：
  $$\mathcal{D}\left({\mathrm{z}}^{\prime },{\mathrm{z}}^{\prime \prime }\right)=\left({\hat{\mathrm{z}}}^{\prime }{\hat{\mathrm{z}}}^{\prime \prime \top }+1\right)/2=\left(\cos \left({\mathrm{z}}^{\prime },{\mathrm{z}}^{\prime \prime }\right)+1\right)/2$$
  其中，$\hat{\mathrm{z}}=\mathrm{z}/\Vert \mathrm{z}\Vert$是二范数表示。
• 损失函数
  通过将$\{({\mathrm{z}}_i^{\prime },{\mathrm{z}}_j^{\prime \prime })|S_{ij}=1\}$视为从联合分布中采样的正样本对，$\{({\mathrm{z}}_i^{\prime },{\mathrm{z}}_j^{\prime \prime })|S_{ij}=0\}$视为从边缘分布乘积中采样的负样本对，总体对比损失可以表示为：
  $$\begin{array}{rl}{\mathcal{L}}_{\mathrm{IA}}& =-\frac{1}{N}\sum _{i=1}^N\sum _{j=1}^N\left[\frac{1}{m_i^{+}}{S}_{ij}\log \left(\mathcal{D}\left({\mathbf{z}}_i^{\prime },{\mathbf{z}}_j^{\prime \prime }\right)\right)\right]\\ & +\frac{1}{m_i^{-}}\left(1-S_{ij}\right)\log \left(1-\mathcal{D}\left({\mathbf{z}}_i^{\prime },{\mathbf{z}}_j^{\prime \prime }\right)\right)\end{array}$$
  其中$m_i^{+}$和$m_i^{-}$分别表示关于${\mathrm{z}}_i^{\prime }$的正样本对和负样本对的个数。
  正样本对：通过最大化 $\mathcal{D}\left({\mathrm{z}}_i^{\prime },{\mathrm{z}}_j^{\prime \prime }\right)$ 使得正样本对（即$S_{ij}=1$）在表示空间中更接近。
  负样本对：通过最小化 $1-\mathcal{D}\left({\mathrm{z}}_i^{\prime },{\mathrm{z}}_j^{\prime \prime }\right)$（即$S_{ij}=0$）在表示空间中更远离。
  由于负样本远多于正样本，对它们的约定分别进行平均有助于缓解不平衡问题。

4.实验

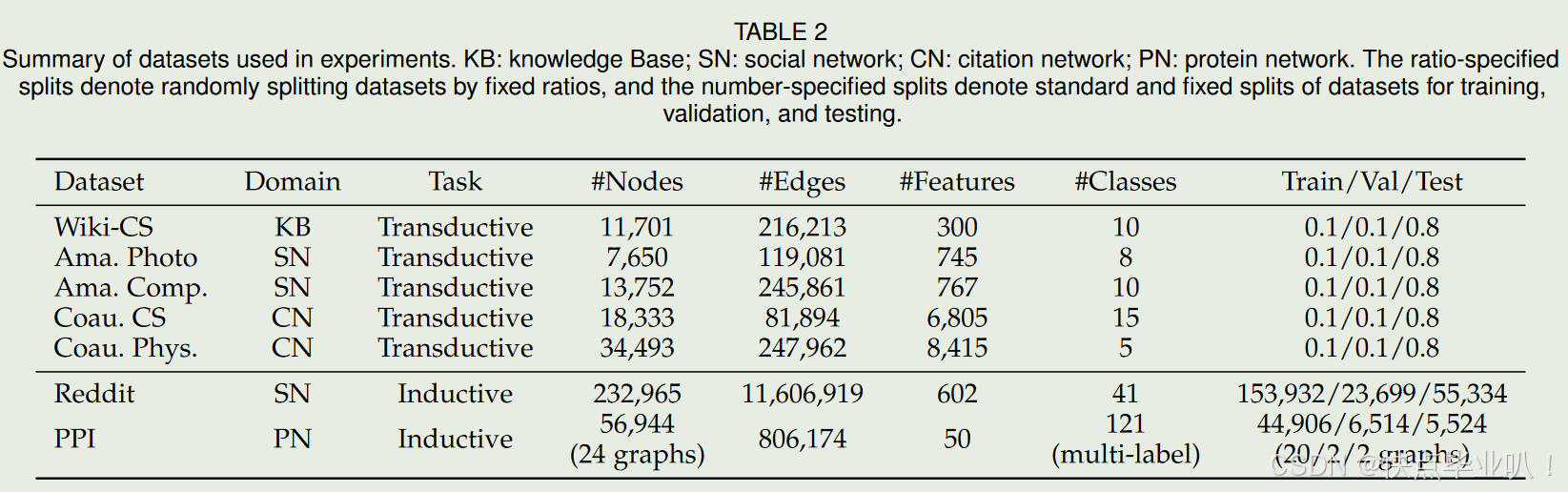
4.1 数据集

4.2 实验结论

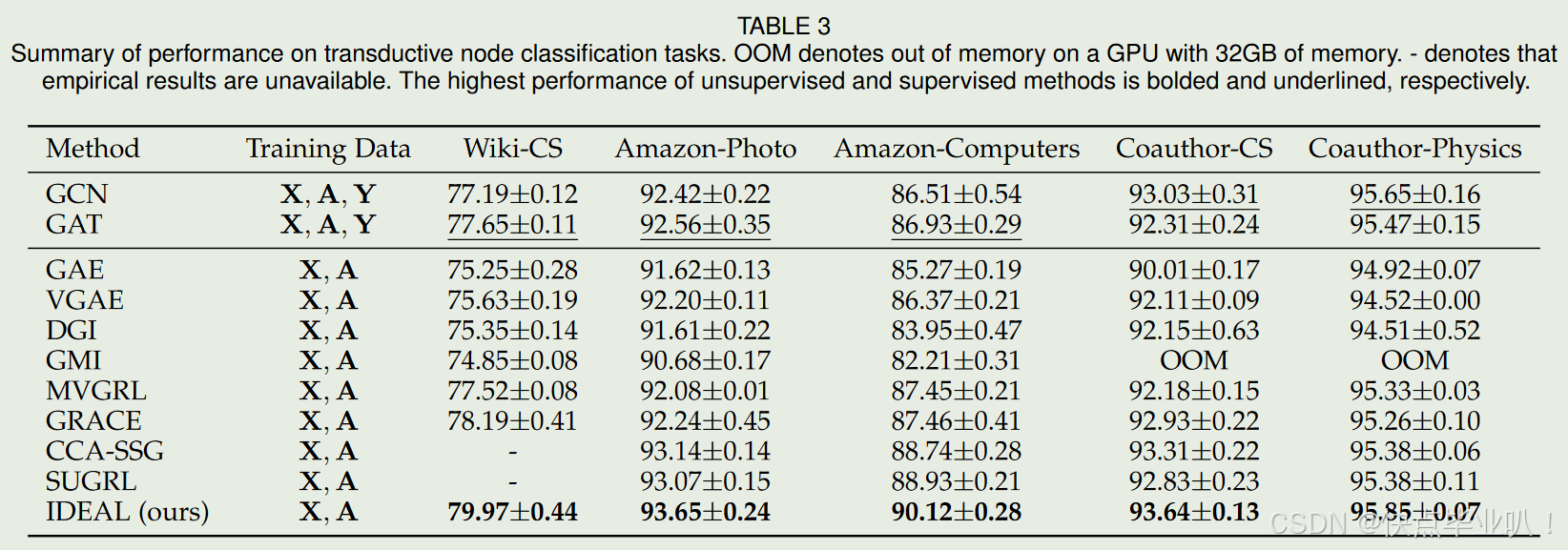
4.2.1 与SOTA方法对比

• 直推式节点分类模型对比
  

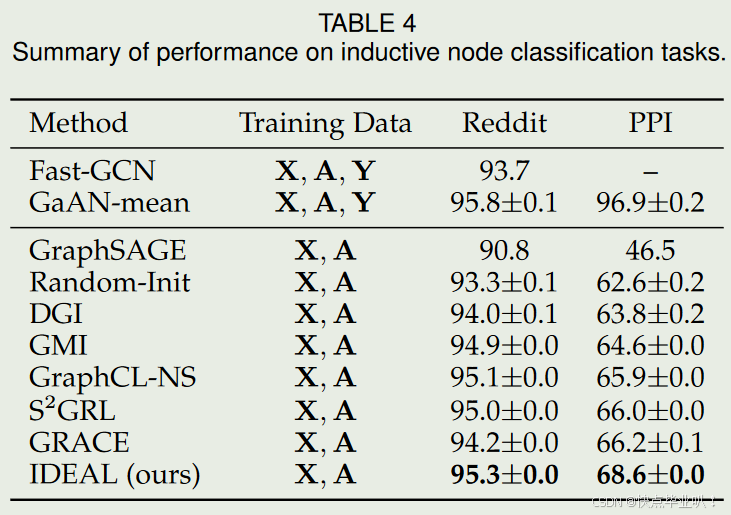
• 归纳式节点分类性能对比

  

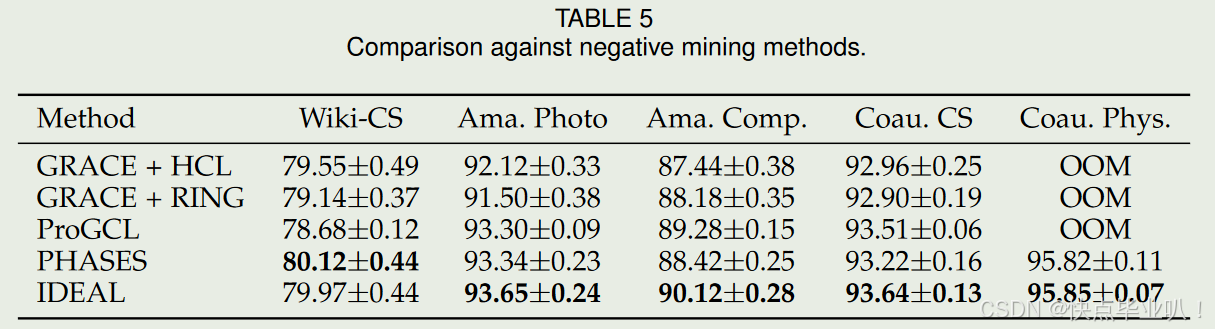
• 与负样本挖掘方法比较
  

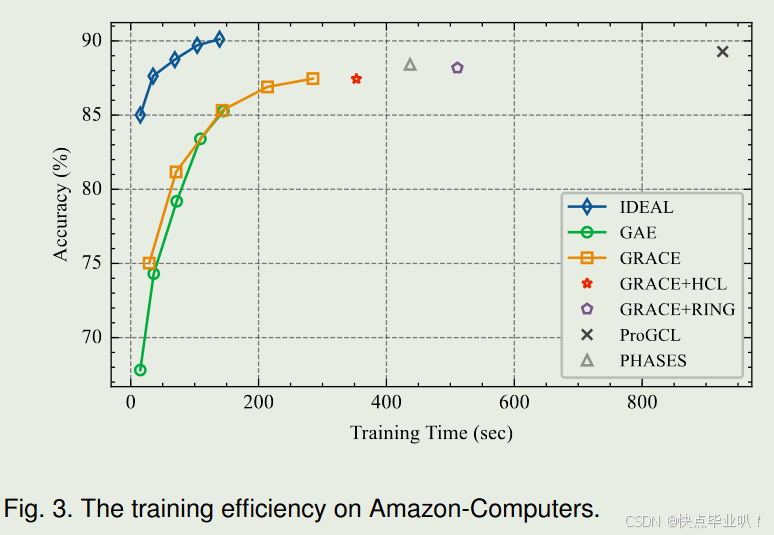
4.2.2 训练效率评估

展示了IDEAL与其他方法（如GAE和GRACE）在训练效率上的比较，证明IDEAL在训练效率上显著优于其他方法，能够在更短的时间内达到更高的准确率。

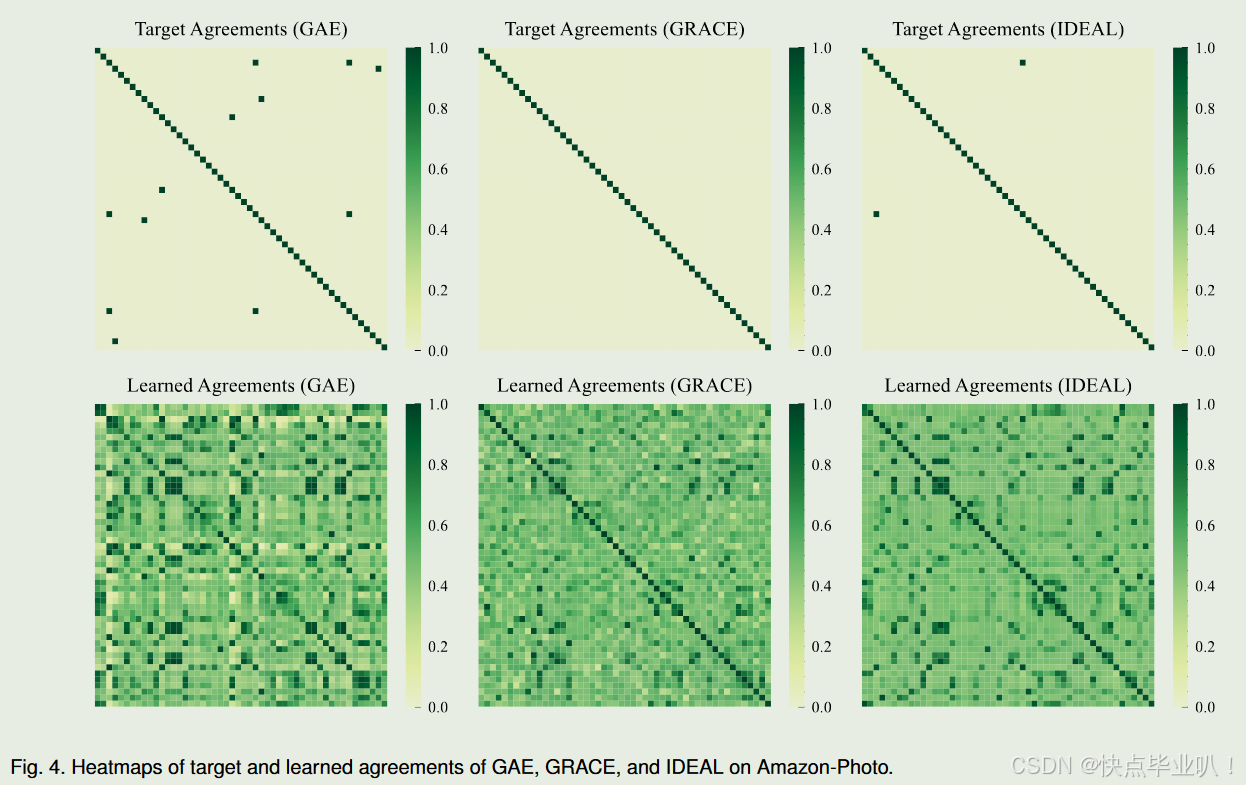
4.2.3 学习和目标一致性可视化

通过热图展示了GAE、GRACE和IDEAL在目标一致性和学习一致性上的差异，证明了IDEAL在学习一致性上更好地保留了拓扑模式和语义信息，同时比GRACE包含更少的噪声。

4.2.4 嵌入质量的分析

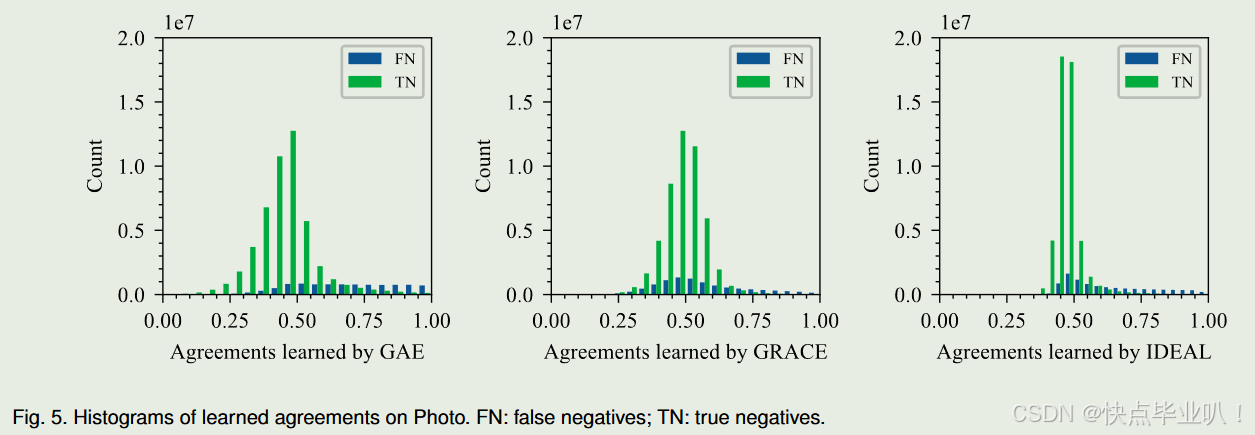
展示了学习一致性的直方图，包括假阴性（false negatives）和真阴性（true negatives），证明了IDEAL在保持假阴性一致性的同时，有效地分离了真阴性，表明其学习到的嵌入分布既全局一致又局部聚集。

4.2.5 消融实验

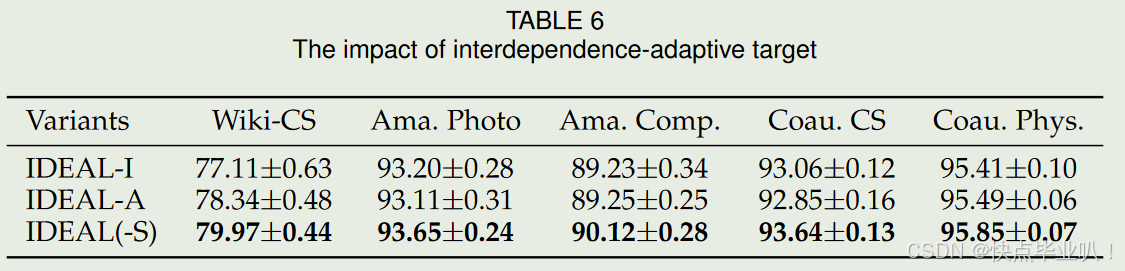
• 相互依赖–适应性目标的影响
  
  研究了目标一致性矩阵的不同设置对IDEAL性能的影响，结论表明IDEAL的相互依赖–自适应方案对于最大化跨视图互信息至关重要。
  
  探讨了不同判别器对IDEAL性能的影响，结论表明IDEAL提出的线性缩放余弦判别器在所有五个数据集上均表现优于其他传统判别器。
  
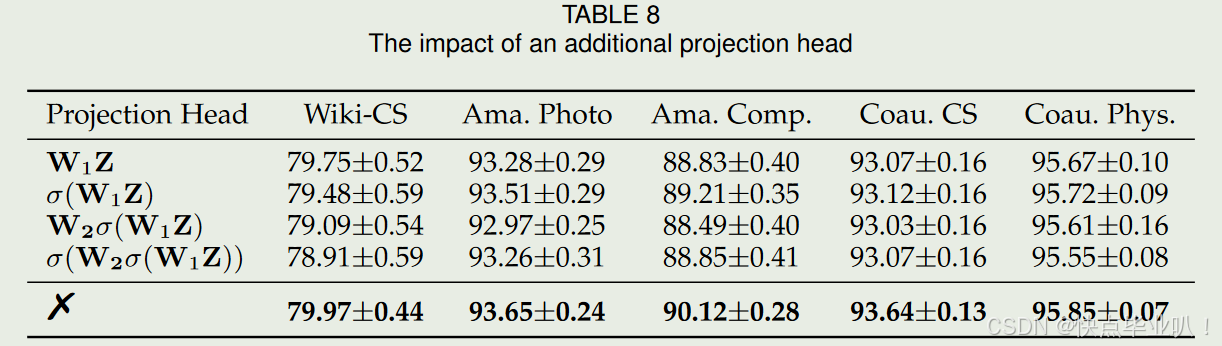
  研究了额外投影头对IDEAL性能的影响，证明在IDEAL中引入额外的投影头会降低下游节点分类任务的性能。

碎碎念：
1.由于论文将不同节点的相互依赖关系视为一个正样本，因此负样本的数量会有一定程度的减少。当负数个数减少时，Jensen-shannon MI估计量( JSD)比KL散度的Donsker - Varadhan表示( DV)更稳定，与噪声对比估计( InfoNCE)相比，Jensen-shannon MI估计量对负样本数不敏感。因此，论文采用了JSD估计量来估计和最大化跨视角互信息。
2.线性缩放余弦判别器的优势
① 与直接计算内积不同，LSC首先将学习到的表示归一化到单位超球上，这对在NT - Xent损失中获得更好的表示是非常关键的
② LSC可以在不借助非线性激活函数的情况下，将分数线性地缩放到 [0,1] 的范围内
③ 由于舍弃了额外的投影头projector，LSC是完全非参数的