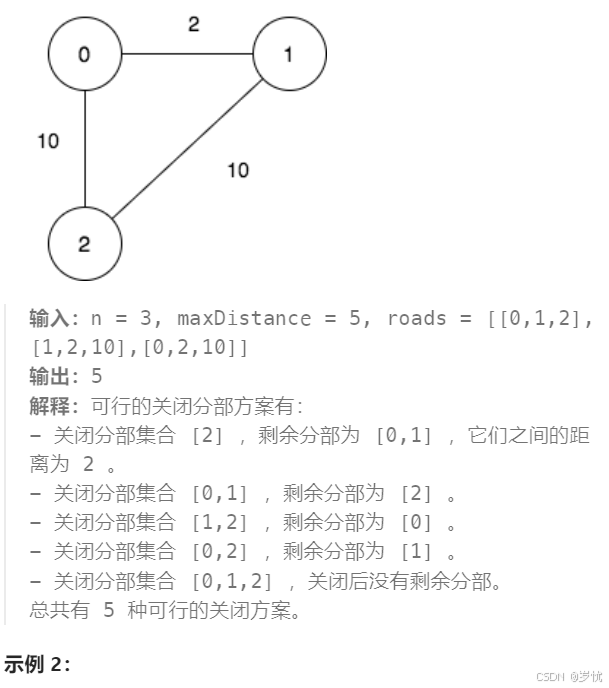
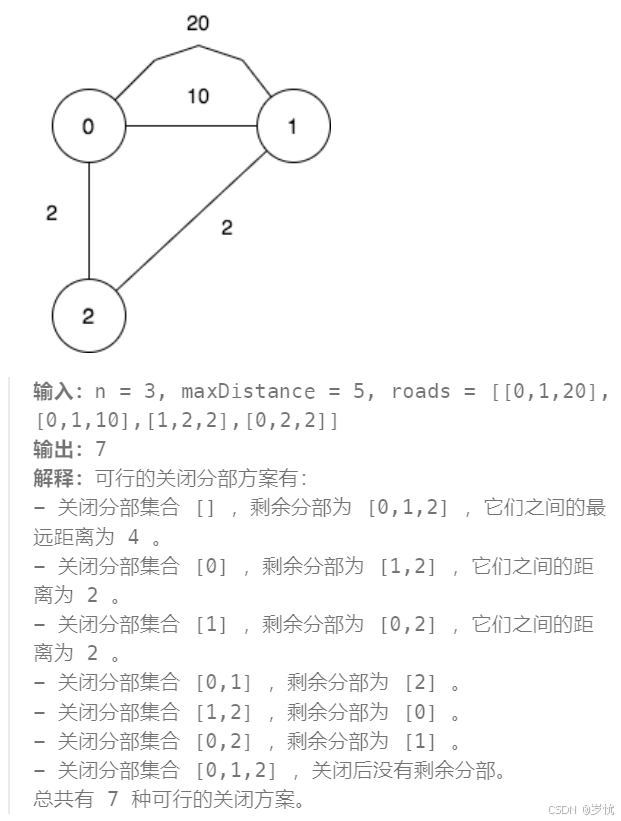
2959. 关闭分部的可行集合数目

思路：二进制枚举+Floyd
1、n的最大值为10，那么我们直接枚举n个点的状态即可（0表示不选、1表示选）。枚举这里的时间复杂度为0(2^n)。
2、使用Floyd算法来计算每个点之间的距离，时间复杂度为(n^3)
3、最后枚举每两个点之间的距离进行判断即可
细节看注释

class Solution {
public:
    bool check(int n,int maxDistance,vector<bool> sta,int dis[15][15]){
    	
        for(int k=0;k<n;k++){
            if(sta[k]==0) continue;
            for(int i=0;i<n;i++){
                if(sta[i]==0) continue;
                for(int j=0;j<n;j++){
                    if(sta[j]){
                        dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
                    }
                }
            }
        }
        bool flag=1;
        for(int i=0;i<n;i++){
            if(sta[i]==0) continue;
            for(int j=0;j<n;j++){
                if(i!=j&&sta[j]){
                    if(dis[i][j]>100000||dis[i][j]>maxDistance){
                        flag=0;
                        break;
                    }
                }
            }
        }
        return flag;
    }
    int numberOfSets(int n, int maxDistance, vector<vector<int>>& roads) {
    	//用邻接矩阵来记录每个分部之间的距离
        int g[15][15];
        memset(g,0x3f,sizeof g);
        for(int i=0;i<roads.size();i++){
            g[roads[i][0]][roads[i][1]]=min(roads[i][2],g[roads[i][0]][roads[i][1]]);
            g[roads[i][1]][roads[i][0]]=min(roads[i][2],g[roads[i][1]][roads[i][0]]);
        }
        //注意分部到自己的距离为0
        for(int i=0;i<n;i++){
            g[i][i]=0;
        }
        //ans用于记录符合要求的方案数，初始为1，是将所有分布都删掉的情况
        int ans=1;
        //二进制枚举所有可能的情况
        for(int i=1;i<(1<<n);i++){
            vector<bool> sta(n,0);
            //找出当前状态下被保留的分部
            for(int j=0;j<n;j++){
                if(i>>j&1){
                    sta[j]=1;
                }
            }
            //复制一份邻接矩阵给dis，好进行Floyd
            int dis[15][15];
            memcpy(dis,g,sizeof g);
            if(check(n,maxDistance,sta,dis)) ans++;
        }
        return ans;
    }
};