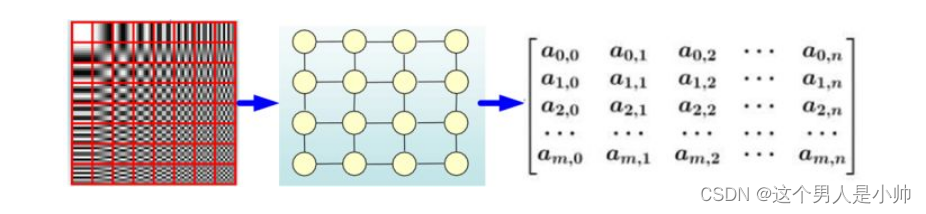
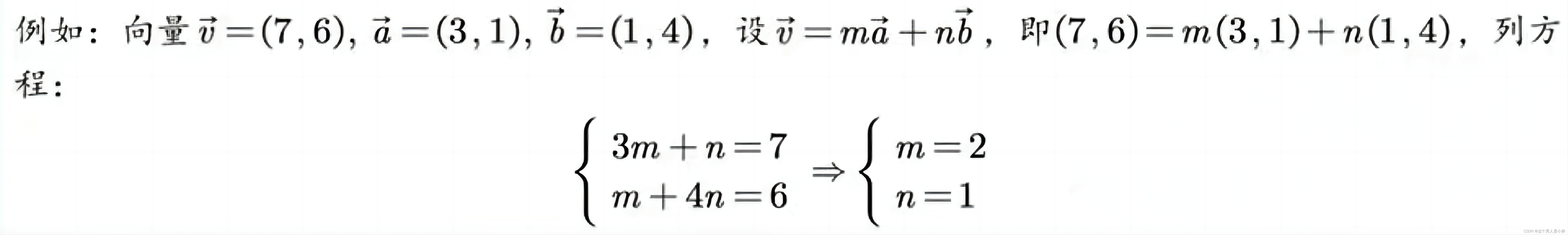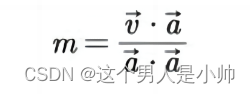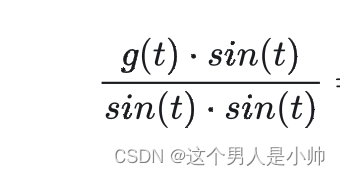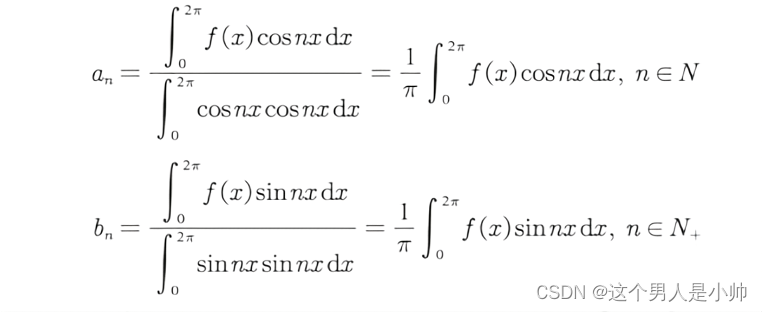文章目录
前言
为了系统化自身的知识体系,并使后续学习谱域图卷积神经网络更为简便、高效,避免不必要的迂回,我撰写了这篇文章。我希望这不仅有助于梳理我个人的思维,也能够为他人提供便利。为了更全面地理解谱域图卷积神经网络,我将文章分为神经网络、卷积神经网络和图卷积神经网络三个主要部分进行引入与讲解。通过对相关知识点的详细解释,希望读者能够建立起对谱域图卷积神经网络的深入理解。
提示:收藏不是学习,请耐心看完哦
一、神经网络
1.1 什么是神经网络?
百度百科的定义是这样的
人工神经网络(Artificial Neural Network,缩写ANN),简称神经网络(Neural Network,缩写NN),是一种模仿生物神经网络(动物的中枢神经系统,特别是大脑)的结构和功能的数学模型或计算模型,用于对函数进行估计或近似。神经网络是一种有监督的机器学习算法,广泛地应用于分类预测、图像识别等领域。
个人理解
简而言之,神经网络是通过可训练的参数来逼近或拟合我们想要的曲线或曲面,从而解决分类或回归问题。可以将其理解为找到一个最佳曲线,以最好地拟合或区分给定的数据点。
1.2 激活函数的非线性之美
“什么是神经网络”中提到了拟合曲线,首先看如何拟合直线呢。直线方程为
y
=
a
x
+
b
y = ax + b
y=ax+b
通过使用类似于直线方程的思想,在神经网络中,我们可以将
y
y
y 视为网络的输出,
x
x
x是输入特征,
a
a
a和
b
b
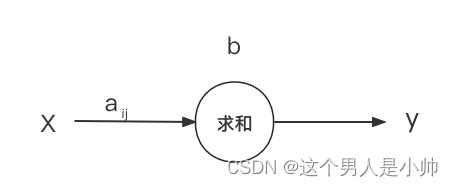
b是该层的权重和偏置直观的理解神经网络的思想。下图为神经元图片:
通过调整
a
a
a和
b
b
b 的值,调整直线的斜率和截距,从而使其更好地拟合数据。在实际的神经网络中,输入
x
x
x 可以是高维度的数据,例如,对于一个个体,可以包括身高、性别、肤色等多个特征作为输入。通过多个特征信息从而输出这个人某一个标签即
l
a
b
e
l
label
label,形成了一个最简单的神经网络模式。
这个模式最大的缺点就是不能够进行非线性数据的拟合,也就是
y
=
a
x
+
b
y = ax + b
y=ax+b的线性模型可能无法捕捉到复杂的非线性关系。对于某些数据,神经网络可能需要更复杂的结构来更好地拟合。
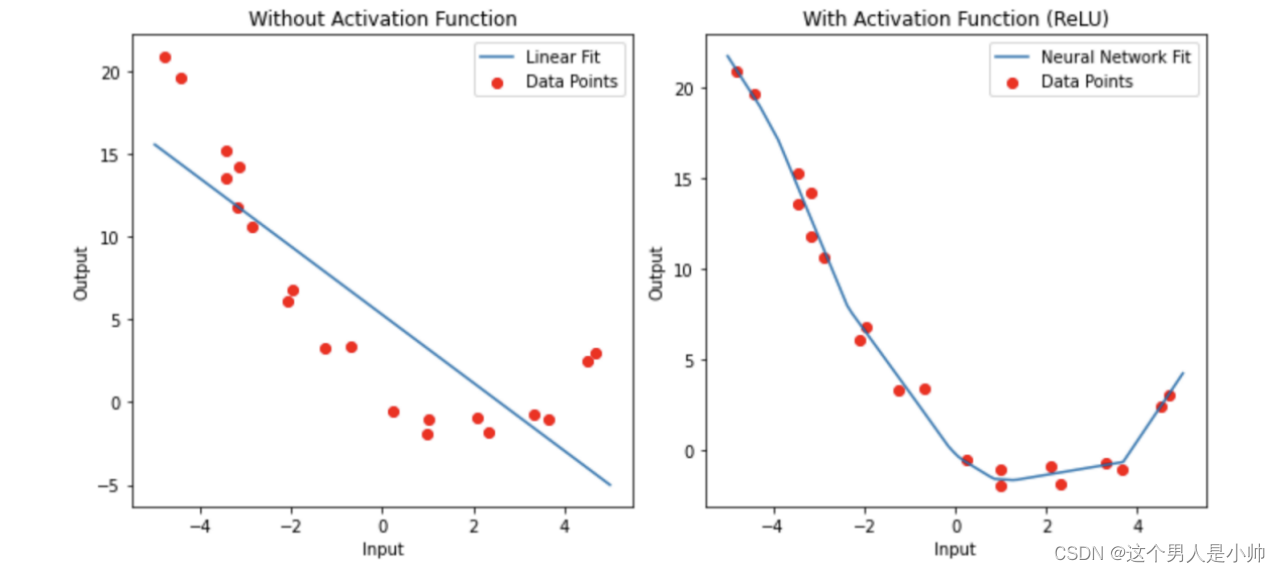
通过下图直观的展示了这一特性,左侧为没有激活函数就是
y
=
a
x
+
b
y = ax + b
y=ax+b,右侧为存在激活函数
y
=
f
(
a
x
+
b
)
y = f(ax + b)
y=f(ax+b).
非线性函数的引入允许神经网络学习并捕捉数据中的非线性关系,使其具备更强大的表示能力。这种能力使得神经网络能够适应各种数据分布,从而更好地拟合实际问题。简单的理解成
a
a
a实际上就是训练的参数也是对特征进行选择,
b
b
b调整模型对激活函数的敏感程度就即(激活函数被激活的容易程度)。
BUT 但是这还不够
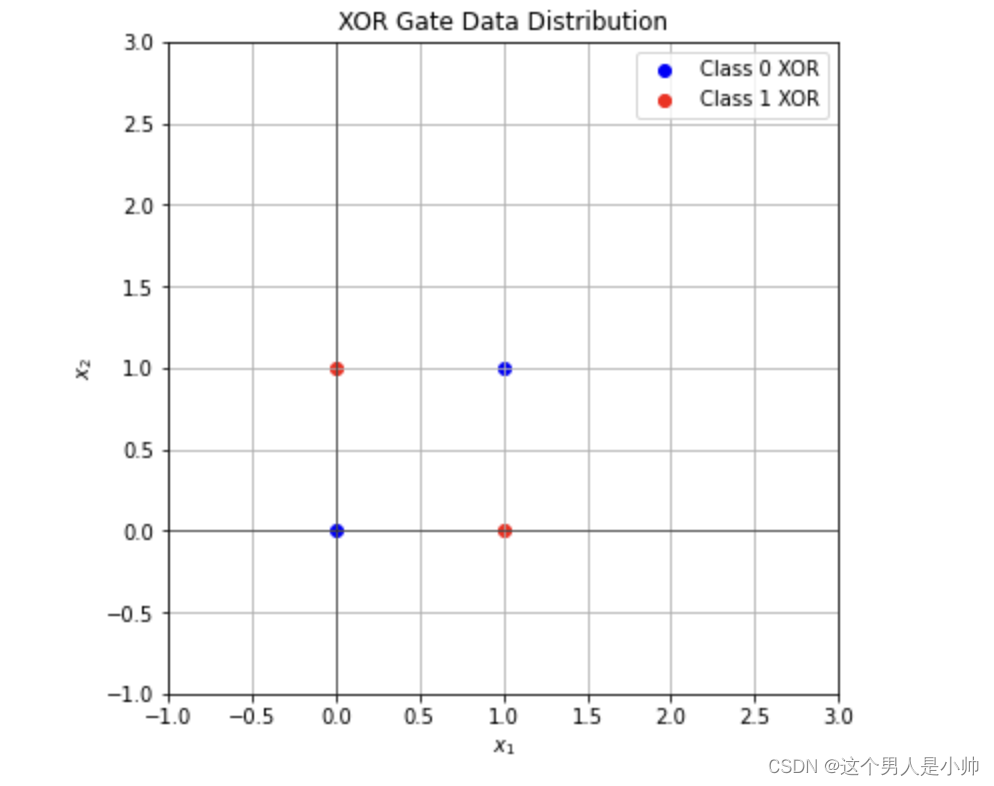
无法正确地学习和拟合 XOR(异或) 问题
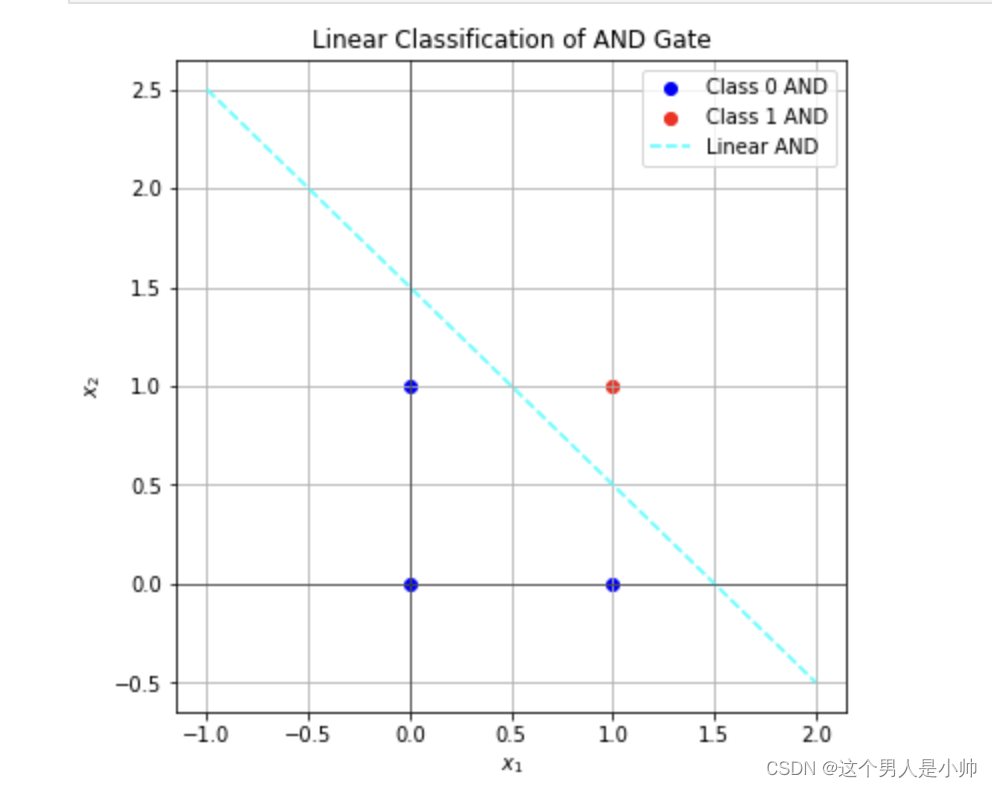
通过线性函数可以很好的划分与,或,非这类数据,下图展示了函数划分 “与” 数据的情况
数据分布情况看下表
| Input (X1, X2) | Output (X1 XOR X2) |
|---|---|
| 0 0 | 1 |
| 0 1 | 1 |
| 1 0 | 1 |
| 1 1 | 0 |
与门、或门和非门三种数据都可以通过简单的线性方式很好地进行划分,但是异或门则难以通过这种方式实现。下面是异或门的数据
| Input (X1, X2) | Output (X1 XOR X2) |
|---|---|
| 0 0 | 0 |
| 0 1 | 1 |
| 1 0 | 1 |
| 1 1 | 0 |
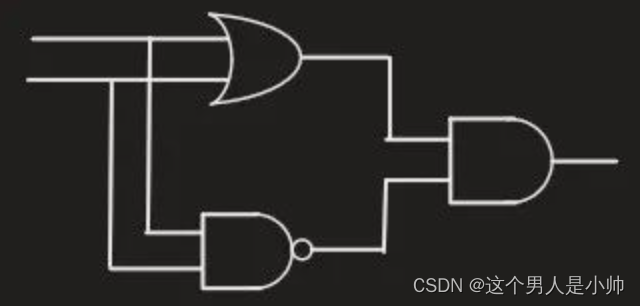
显然单一的线性方式无法实现对 XOR gate 的划分,但通过逻辑门的组合,我们可以构建一个包含 XOR gate 的复合逻辑。例如,我们可以通过组合 AND gate、OR gate 和 NAND gate 来实现 XOR gate。
XOR(A, B) = AND(NAND(A, B), OR(A, B))。实际情况可以看下图展示的情况。
这个表达式说明了如何通过 AND、OR 和 NAND逻辑门的组合来实现 XOR gate。通过这种方式,我们能够建立一个非线性的关系,从而成功划分 XOR gate 的输入空间。因此,尽管单一的线性方式难以实现 XOR gate 的划分,但通过巧妙地组合多个逻辑门,仍然能够实现这一目标。
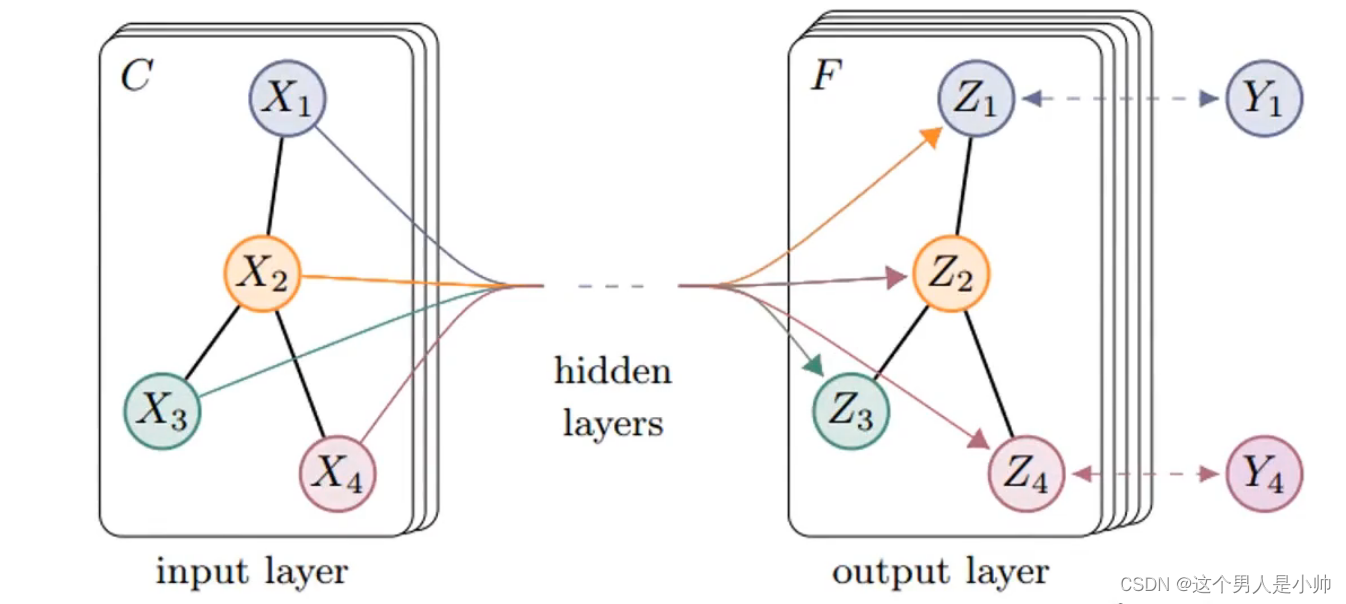
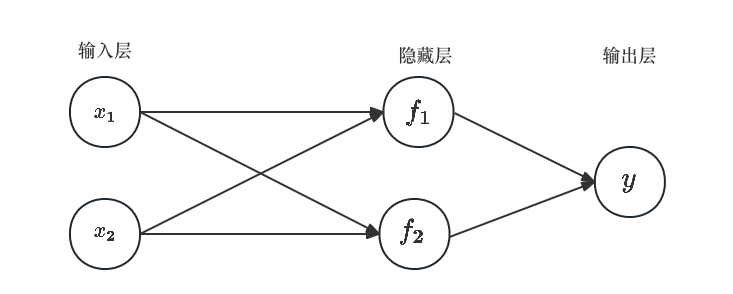
即(最开始的神经网络只有输入层和输出层,加了隐藏层性能提升巨大)
就是感知机(Perceptron)和多层感知机(Multilayer Perceptron,MLP)的差别)
这个图看起来怎么有些熟悉呢??
通过简单神经网络的表示和上面的图对比下看看。
一模一样
两个简单的神经网络(也可以看作是逻辑门)的输入和输出,然后再将这两次的输出进行组合,再次进行加权求和激活函数这一流程,实际上就是构建了一个包含多层结构的神经网络,通常称为多层感知机(Multi-Layer Perceptron,MLP)或深度神经网络(Deep Neural Network,DNN)。
在实际上应用中,真正的神经网络需要根据具体任务选择合适的激活函数、层数以及超参数。这个过程涉及到仔细的设计和调整,通过反向传播算法和损失函数的优化迭代,最终形成一个能够有效学习和表示复杂关系的神经网络结构。这种细致的调整和优化是构建出真正有效神经网络的关键要素。
二、卷积神经网络
2.1 为什么要有卷积神经网络呢?
首先要了解卷积神网络之前我们要了解下神经网络在图片处理领域的缺点有哪些:
- 参数量庞大: 对于高分辨率的图像,全连接神经网络的参数量会非常庞大,导致训练和推理过程需要更多的计算资源。
- 例如:在一个全连接神经网络中,会将高维度的数据拉成一维数据,进行输入,如果输入是一个100x100像素的图像,并且每个像素有三个通道(RGB),那么输入层的节点数是100 * 100 * 3 = 30,000。如果第一个隐藏层有100个神经元,那么与输入层相连的权重和偏置参数的总数是30,000 * 100 + 100 = 3,000,100。需要训练的参数量太过巨大,对计算的计算性能以及训练样本量都是巨大的挑战,还容易引发过拟合。
- 平移不变性: 全连接神经网络在处理平移变换时可能会缺乏不变性,即使图像中的物体平移一小部分,网络可能需要重新学习相应的特征。
- 数据需求量大: 神经网络通常需要大量标记的数据进行训练,而在图像领域,标记大规模数据集可能非常耗时和昂贵。
- 对空间结构的理解有限: 图像是三维形状,这个形状中应该包含重要的空间结构信息。
- 例如:空间中相邻的像素是相似的值、RGB的各个通道之间有密切的关联性,距离较远的像素之间没有什么关联,三维形状中可能存在着值得提取的本质模式。但是全连接神经网络会忽视形状,将全部的输入数据作为相同的神经元处理,所以无法利用与形状相关的信息。
因此要设计一种专门针对图像结构(Image)的神经网络。由此出现了卷积神经网络。 - 例如:想象一下相邻的像素之间存在相似性的关联。当我们看到一张猫的照片时,猫的眼睛可能是黑色的。因此,其中一个像素是黑色的话,周围的像素颜色很可能也接近于黑色数值。
因此孤立的看待数据容易忽视形状结构之间的关联,不利于特征的提取。
2.1 什么是卷积神经网络呢?
卷积神经网络(Convolutional Neural Network,CNN)是一种带有卷积层和池化层的神经网络。下面的图示比较了卷积神经网络和传统神经网络,上方的是神经网络,下方是卷积神经网络。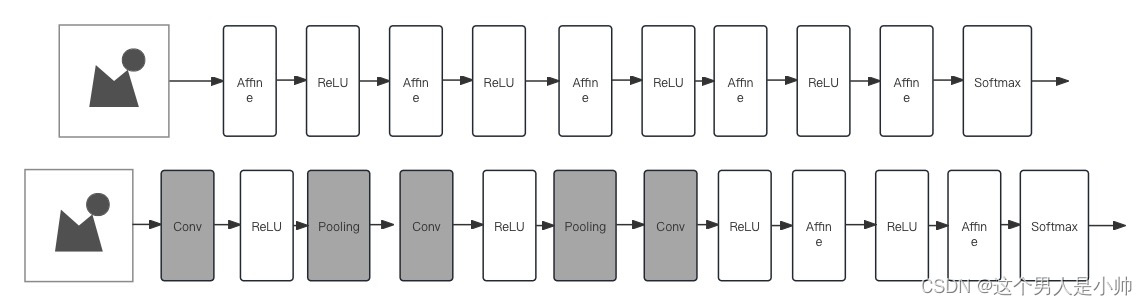
即针对图像结构设计的增加卷积和池化层的神经网络。
2.2 什么是卷积呢?
提到"卷积"这个词可能会感到陌生,但如果是"加减乘除",这只是对某种运算方式的称呼。接下来介绍一下卷积运算。
就像
a
+
b
a + b
a+b 是加法运算一样,抽象的卷积运算也有类似的表示方式。卷积的公式如下:
(
f
∗
g
)
(
n
)
(f*g)(n)
(f∗g)(n)只是这个公式涉及到了积分的运算变得很复杂而已。在离散形式和连续形式的的公式是如下
(
f
∗
g
)
[
n
]
=
∑
m
=
−
∞
∞
f
[
τ
]
⋅
g
[
n
−
τ
]
(f * g)[n] = \sum_{m=-\infty}^{\infty} f[ \tau] \cdot g[n - \tau]
(f∗g)[n]=m=−∞∑∞f[τ]⋅g[n−τ]
(
f
∗
g
)
(
n
)
=
∫
−
∞
∞
f
(
τ
)
⋅
g
(
n
−
τ
)
d
τ
(f * g)( n) = \int_{-\infty}^{\infty} f(\tau) \cdot g(n - \tau) \, d\tau
(f∗g)(n)=∫−∞∞f(τ)⋅g(n−τ)dτ
看起来复杂实际上就是对不同位置的数值进行加权求和
举个大家都在用的例子便于大家理解。
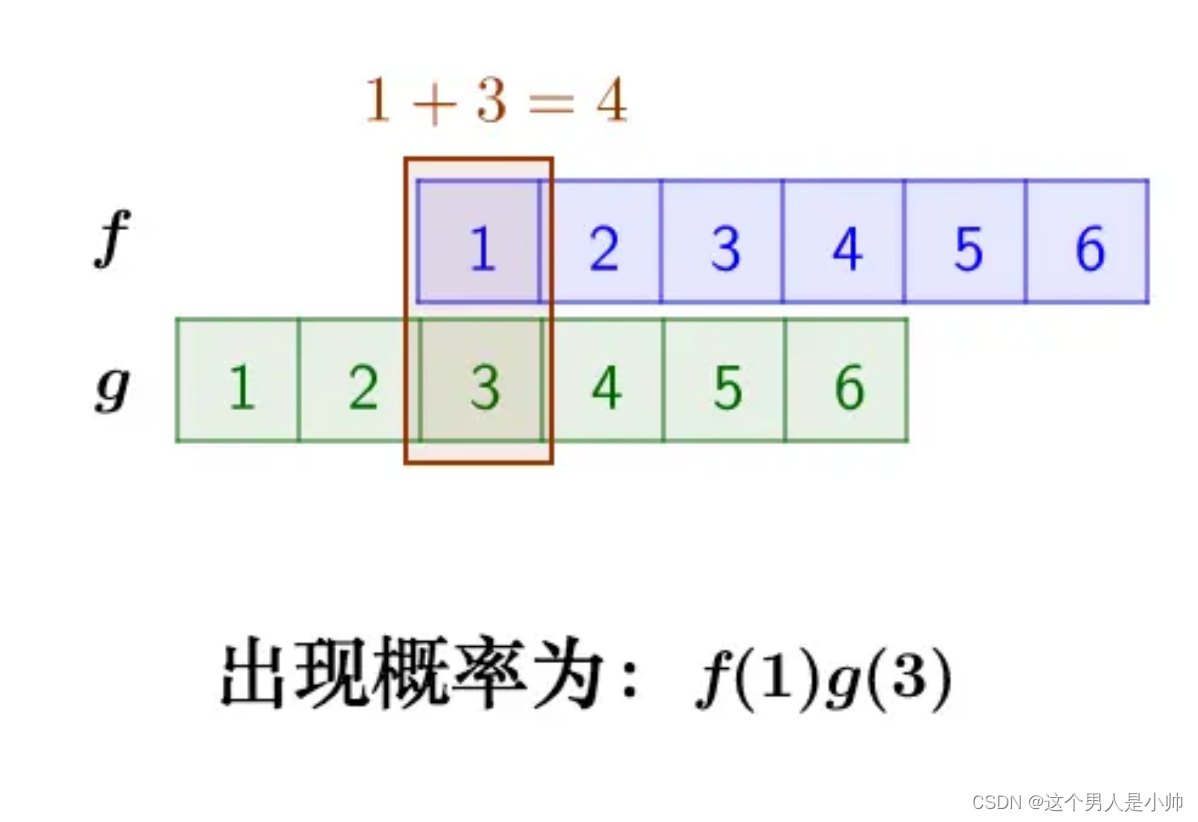
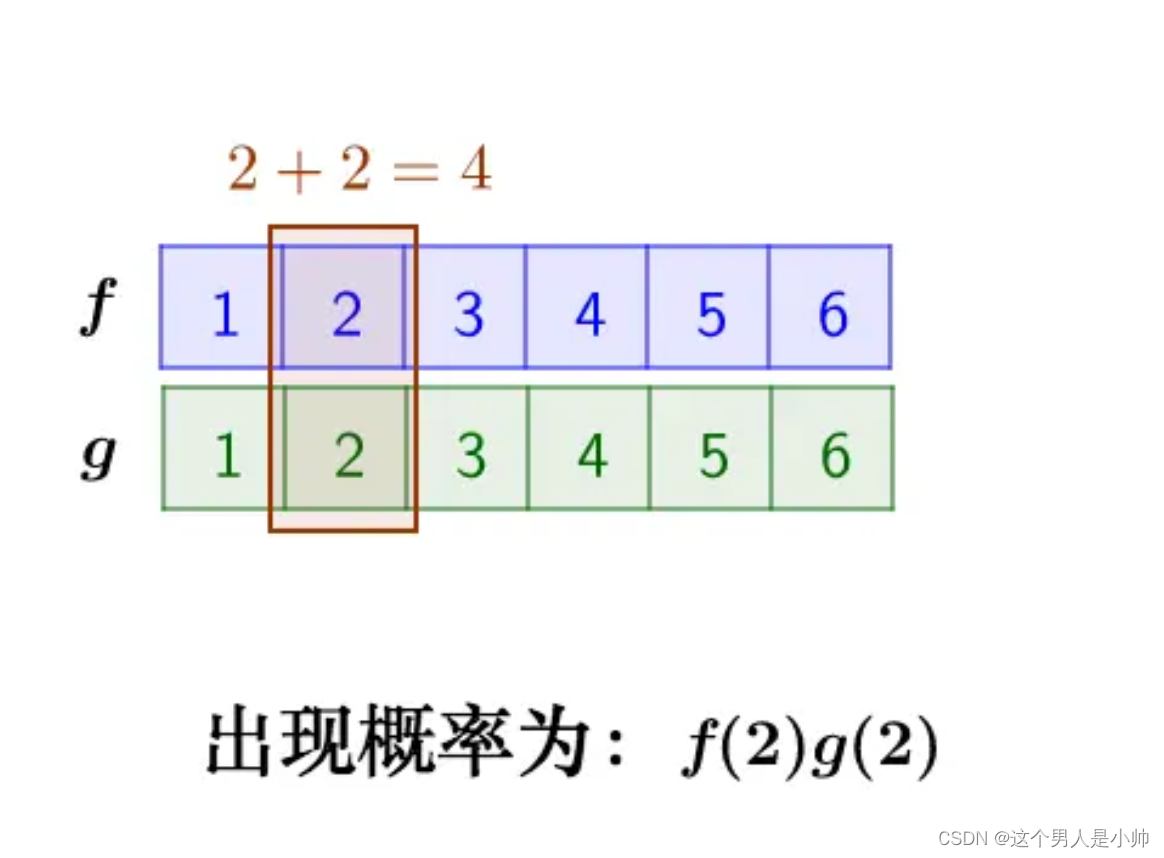
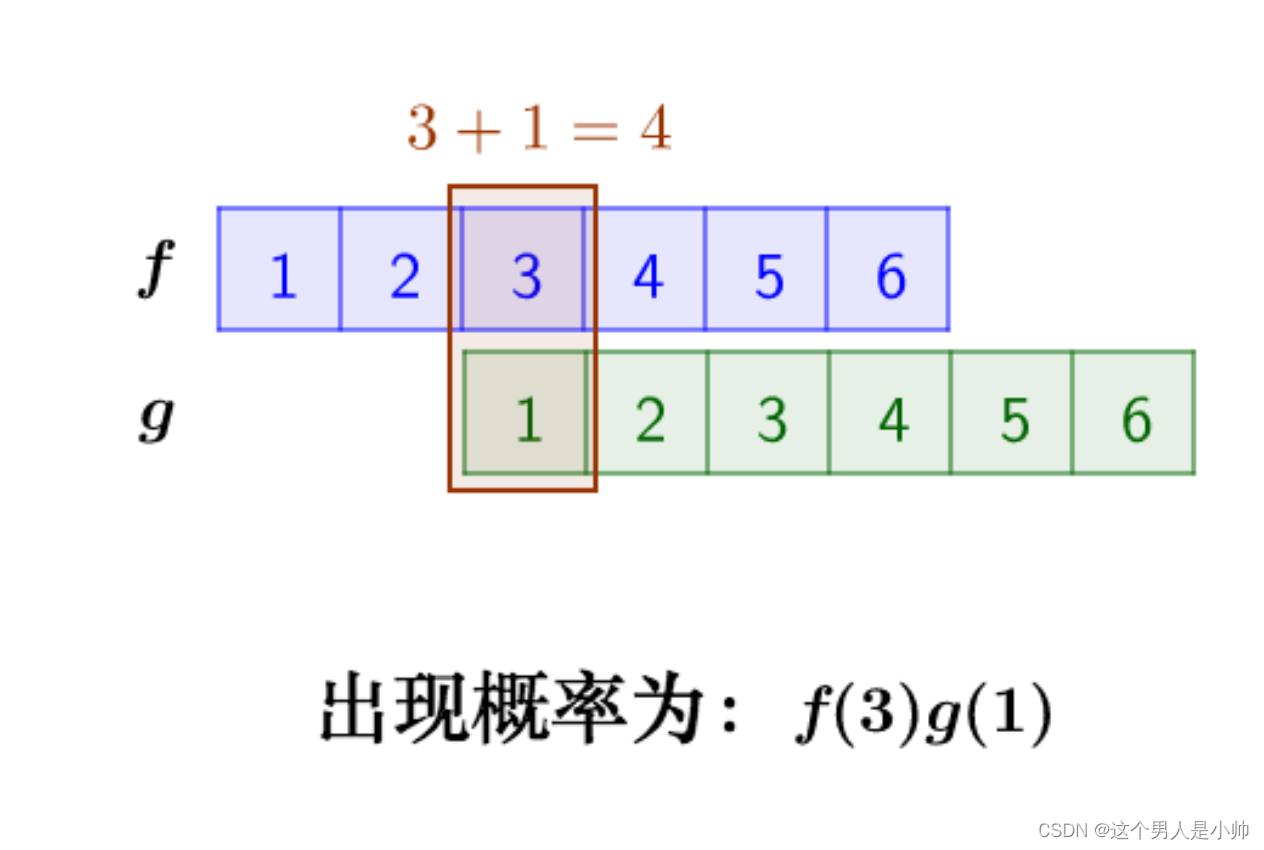
两个骰子:把两个🎲骰子同时丢出去。求两个骰子点数加起来为4的概率是多少呢?
问题的关键在于,两个骰子的点数加起来等于4。这就是卷积的一个应用场景。我们可以通过计算不同点数出现的概率,并用函数表示出来。
那么两个骰子点数加起来为4的情况是:
因此两个骰子加起来点数为4的概率就是为:
f
(
1
)
g
(
3
)
+
f
(
2
)
g
(
2
)
+
f
(
3
)
g
(
1
)
f(1)g(3)+f(2)g(2)+f(3)g(1)
f(1)g(3)+f(2)g(2)+f(3)g(1)
是不是有点眼熟了
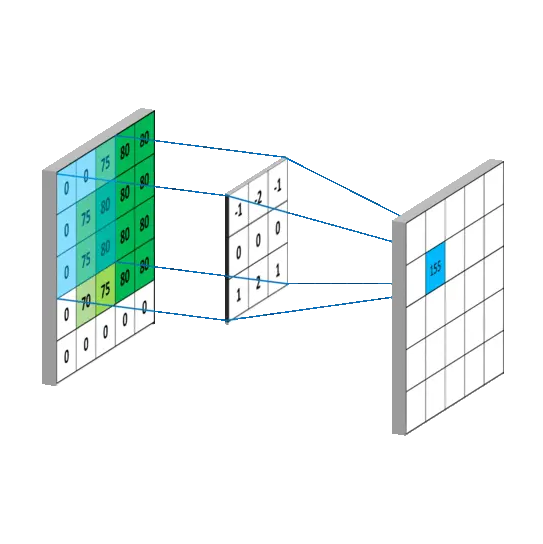
不断滑动的窗口对应位置进行加权求和,这实际上就是CNN的卷积层。在这个过程中,对当前位置的特征进行加权,
f
(
x
)
f(x)
f(x) 相当于特征,
g
(
x
)
g(x)
g(x) 则相当于权重,也就是卷积核。只不过这个操作是在矩阵上进行的。当然,这并不是非常严谨的说法,但是为了方便大家理解,概念上是相通的。懂就行。
在CNN中,卷积操作与数学上的传统卷积有一些不同。总体而言,CNN中的卷积是一种用于学习特征的操作。它引入了权值共享和参数可学习的特性,使得CNN能够更好地适应图像处理任务,并通过共享权值降低了模型的复杂度。这些特性使得CNN在处理大规模图像数据时更加高效和有效。
参数学习: 在CNN中,卷积核的权重是可以学习的,这意味着网络可以通过反向传播算法来自动调整这些权重以适应任务。而数学上的卷积通常是基于预定义的核或函数。
权值共享:是CNN中的一个重要特性。在数学中,卷积操作通常涉及两个函数的卷积,而且这两个函数的权值是独立的参数。然而,在CNN中,我们采用具有共享权值的卷积核。这意味着卷积核的权值在整个输入图像上是共享的,即使用一个卷积核对整个图像进行加权求和。这种权值共享有助于减少模型的参数数量,提高模型的训练效率,并使网络更容易泛化到新的数据。
稍微唠叨下
人类看图片某一个区域实际上这个区域的颜色应该是都差不多的,所以存在着特定关联。
卷积核就像我们之前看到的线性函数中的参数
a
a
a,用于提取特征。然而,CNN的特殊之处在于,下一层的特征是由上一层的邻居和自身本身的特征加权得到的。这使得得到的特征具备了邻域信息,也就是说,它包含了形状信息。这是CNN的一个有趣之处。为什么要采用多个卷积核呢?因为每个卷积核,即每组参数
a
a
a,在优化的过程中对特定特征的偏好是不一样的,也就是它们关注的点不同。需要调整不同的视角关注不同的信息,这就解释了为什么需要多个卷积核一起运算。这部分有点口语化,但为了更好地让读者理解。
2.2 稍微说下什么是池化层呢?
在卷积操作结束后,确实产生了大量的特征信息,而池化层的主要目的是对这些特征进行下采样,即减少数据量(例如,通过取最大值来忽略其他零散的信息),从而降低计算成本并保留最显著的特征。池化层有助于简化网络结构、提高计算效率,并增强模型的泛化能力。主要有两种类型的池化层,分别是最大池化和平均池化。可以将其比喻为对图片进行马赛克处理,虽然细节减少了,但大致的样子我们仍然能够识别是什么东西。这种处理减少了运算成本,同时增加了模型的泛化能力。
最大池化:
在最大池化中,每个池化窗口(通常是2x2或3x3)内的最大值被保留,而其余数值被忽略。这样可以确保每个池化区域仅保留最显著的特征,有助于保留图像中的重要信息,同时减小特征图的空间尺寸。
平均池化:
在平均池化中,每个池化窗口内的数值取平均值,以降低局部变化的影响,从而更强调特征的整体性。平均池化同样有助于减小特征图的维度,减轻计算负担。
通过池化操作,网络可以在减少数据量的同时,保持对图像中重要特征的感知。这样的降维和保留显著特征的操作有助于提高网络的计算效率,减少过拟合的风险,并且使得网络对输入的变换更加鲁棒。
总体而言,卷积层通过特征提取,而池化层则通过下采样和筛选,共同协作以实现对图像信息的高效处理和表示学习。
三、图卷积神经网络
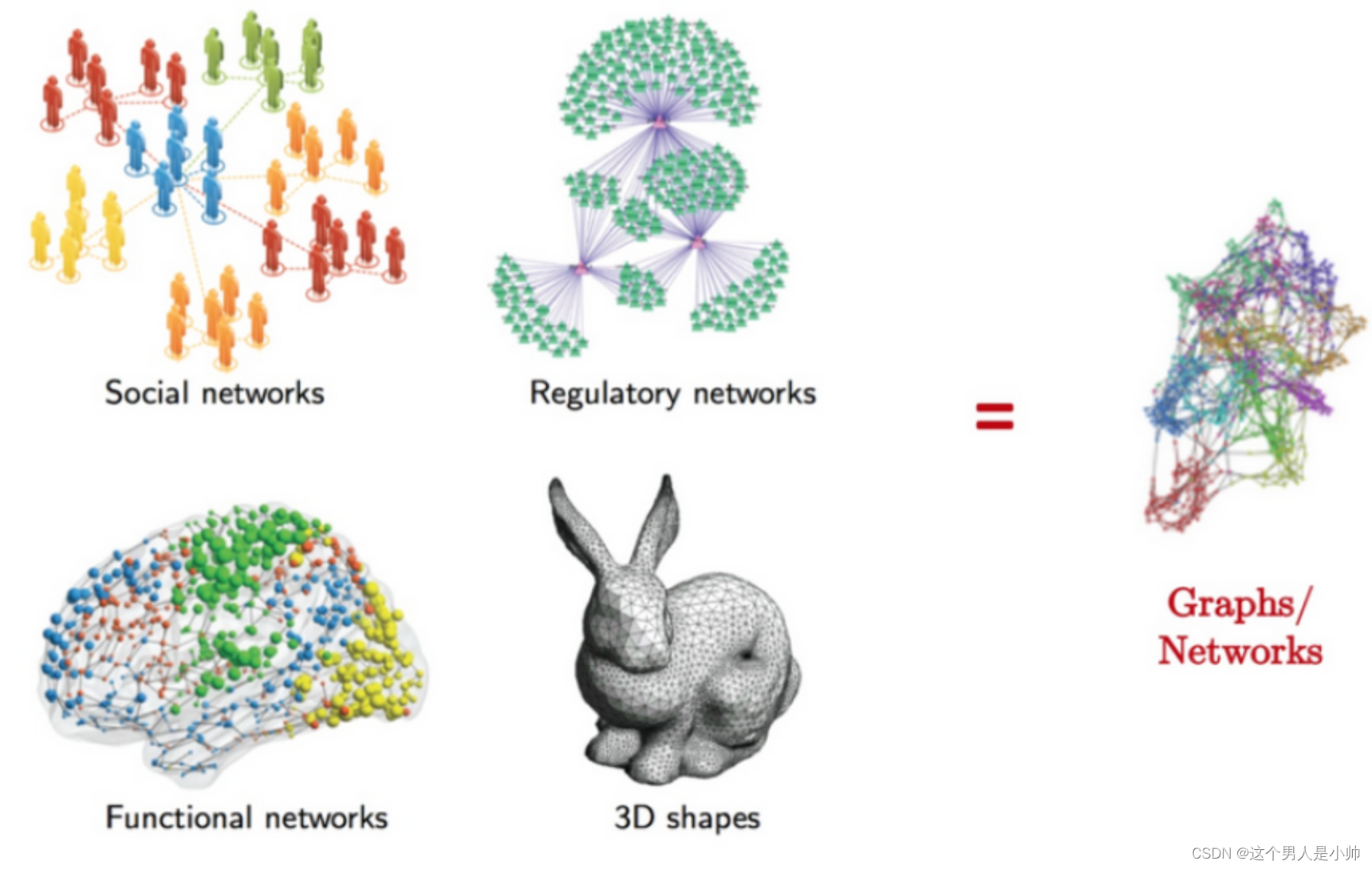
3.1 为啥有图卷积操作?
卷积神经网络(CNN)在计算机视觉领域取得了显著的成功,主要应用于图像处理和图像识别。设计的卷积核通常是规则的矩形,这种结构适用于处理图像的规律性和局部相关性。
规则的欧几里得数据
然而,在图结构(Graph)领域,情况确实较为复杂。图是由节点和边组成的,而节点的邻居个数可以是不同的,图的结构可能是非规则的、稀疏的,且不同节点可能有不同数量的邻居。这样的不规则性和灵活性使得传统的卷积操作不太适用于图数据。
也就是CNN处理欧几里得数据,GCN处理非欧几里得数据。
在图神经网络(Graph Neural Network,简称GCN)中,与卷积神经网络(CNN)处理欧几里得数据不同,GCN专门用于处理非欧几里得数据。CNN的卷积核通常是固定大小的,但在社交网络等非欧几里得数据的情境下,节点的邻居个数可能会变化,如果卷积核大小固定,则可能无法充分捕捉到多余的邻居信息。为了解决这个问题,需要设计一种能够自适应非欧式距离中的卷积核,以有效聚合邻居消息。这使得GCN能够更灵活地适应不同节点邻居的情况。
3.2 如何实现在图上的卷积操作呢?
在学习卷积操作后,很难想象如何将卷积操作应用于图结构。然而,有一种令人惊讶的发现是,卷积操作与傅立叶变换之间存在一种关系。
(
f
∗
g
)
=
F
−
1
(
F
(
ω
)
⋅
G
(
ω
)
)
(f * g) = F^{-1}(F(\omega) \cdot G(\omega))
(f∗g)=F−1(F(ω)⋅G(ω))
卷积操作可以通过两个函数的傅立叶变换的乘积再进行逆变换得到的。
因此先学习傅立叶变换
3.2.1 傅立叶变换
让我们请傅立叶大哥展示才华。
一个人(拉格朗日一众数学家)提出了一个猜想那就是某些周期函数可以由三角函数的和表示。
一步到位了
咱的傅立叶大哥直接猜想了任何周期函数都可以写成三角函数之和表示。
3.2.1.1 如何构成这个表达式呢
首先需要哪些条件构成猜测这个表现形式。
- 需要有常数项—可以改变函数的均值大小,就是那个 y = a x + b y=ax+b y=ax+b的 b b b的作用.
- 已知任意函数都可以分解成奇函数和偶函数的和,而且由于是周期函数,需要同时包含 c o s ( x ) cos(x) cos(x) 和 s i n ( x ) sin(x) sin(x)。
- 要调整震动幅度,可以在 c o s ( x ) cos(x) cos(x) 前面加上一个系数,以确保震动幅度是可控的。
最终公式就是
f
(
t
)
=
a
0
+
∑
n
=
1
∞
[
a
n
cos
(
2
π
n
t
T
)
+
b
n
sin
(
2
π
n
t
T
)
]
f(t) = a_0 + \sum_{n=1}^{\infty} \left[ a_n \cos\left(\frac{2\pi nt}{T}\right) + b_n \sin\left(\frac{2\pi nt}{T}\right) \right]
f(t)=a0+n=1∑∞[ancos(T2πnt)+bnsin(T2πnt)]
符合之前的分析
- 有常数项
- 奇函数和偶函数可以组合出任意函数
- 周期为 T T T
- 调整振幅,逼近原函数
具体该如何确定
a
0
,
a
n
,
b
n
a_0,a_n,b_n
a0,an,bn 直接计算不好确定。
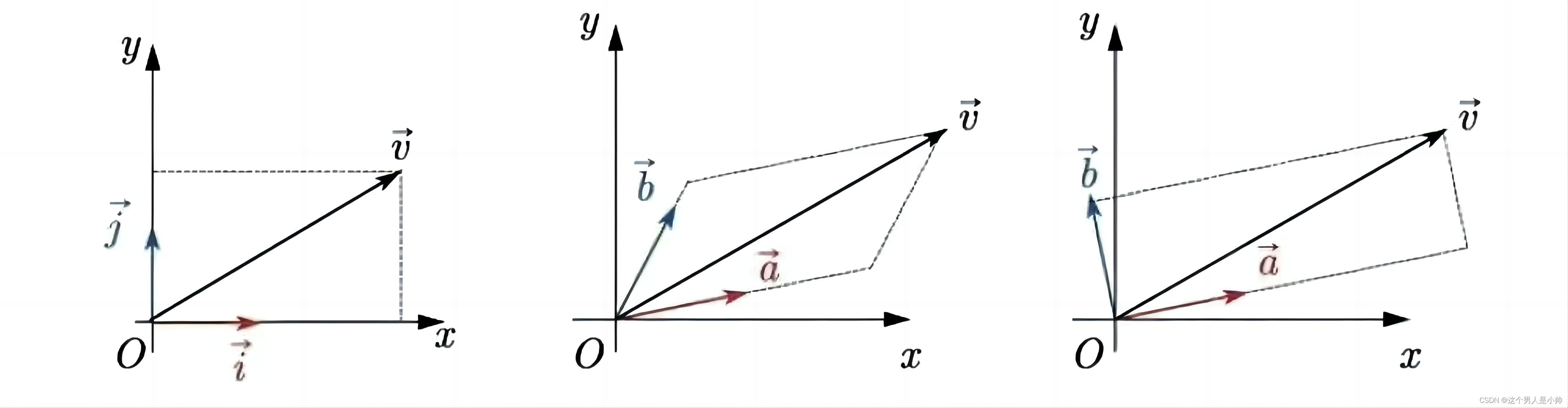
先来关于向量权重的计算方法吧
在平面直角坐标系中,一组正交基(通常选择单位向量就是i为(1,0),j为(0,1))可以用来表示二维空间中的所有点。如果一个点的坐标是
(
x
,
y
)
(x, y)
(x,y),那么与之对应的向量可以表示为
x
i
+
y
j
x\mathbf{i} + y\mathbf{j}
xi+yj。这种表示方式是通过在基向量上乘以相应的坐标来得到的:
v
=
x
i
+
y
j
\mathbf{v}=x\mathbf{i} + y\mathbf{j}
v=xi+yj
可以直观地看出,
(
x
,
y
)
(x, y)
(x,y) 是在基向量上的坐标,即对基础向量的缩放权重。换成
a
a
a 和
b
b
b 更容易理解,一个向量可以表示为两个基向量的加权求和。
更一般地,在平面上,通过对不共线的向量进行加权求和,可以表示出平面的任何一个向量。我们将这组向量称为该平面空间的基,即这个空间的基础是通过这两个向量构造的。
已知这三条向量如何求出权重呢?通常可以使用线性代数中的矩阵方法,通过解线性方程组来求解。
如果f(t) sinx cosx是向量,并且 sinx cosx是一组正交基的话,那前面的系数求解就相对很简单 。
下面的公式别忘了。
f
(
t
)
=
a
0
+
∑
n
=
1
∞
[
a
n
cos
(
2
π
n
t
T
)
+
b
n
sin
(
2
π
n
t
T
)
]
f(t) = a_0 + \sum_{n=1}^{\infty} \left[ a_n \cos\left(\frac{2\pi nt}{T}\right) + b_n \sin\left(\frac{2\pi nt}{T}\right) \right]
f(t)=a0+n=1∑∞[ancos(T2πnt)+bnsin(T2πnt)]
3.2.1.2 欧拉公式
通过欧拉公式进行迂回的求解。
首先验证下f(t) sinx cosx是向量并且 sinx cosx是一组正交基的猜想。
下面是阐述欧拉公式的理解
e
i
θ
=
cos
(
θ
)
+
i
sin
(
θ
)
e^{i\theta} = \cos(\theta) + i \sin(\theta)
eiθ=cos(θ)+isin(θ)
为了更容易理解欧拉公式,让我们一步步来看这个公式。
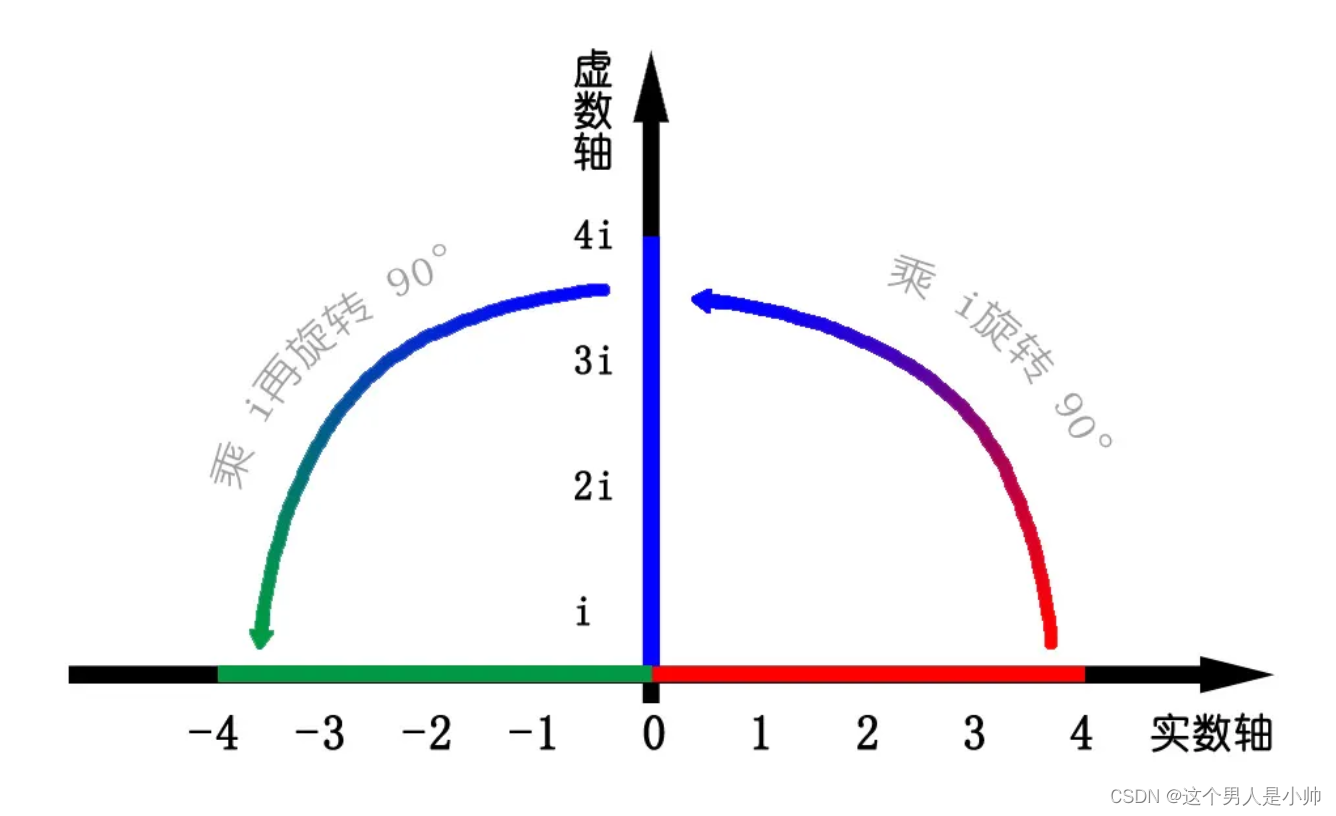
首先,我们要理解什么是复数。 什么是复数? 一个简单的理解方式,这个 i i i复数也不要怕。最直观的理解就是旋转 4 ∗ i ∗ i = − 4 4*i*i = -4 4∗i∗i=−4从而构造了一个关于复平面也就是一个新的坐标系,用来描述平面中向量的坐标。
我们使用复数形式 x + yi 来表示点的坐标。这与常规的直角坐标系类似,只不过这里的 y 轴被称为虚数轴,用 i 来表示。通过这种表示方式,我们可以方便地用复数进行旋转、缩放等操作。
因此,在复平面中,一次乘以 i 相当于将对应的点旋转了90度。这种视角有助于我们理解复数的运算和几何意义。对这样的坐标系我们称之为复平面,其中复数的实部对应于 x 轴,虚部对应于 y 轴。
这种表达方式在复数和复数平面的理解中非常常见,使得复数的运算更加直观。
为什么两个三角函数相加会是指数函数的复数形式呢?
e
i
θ
=
cos
(
θ
)
+
i
sin
(
θ
)
e^{i\theta} = \cos(\theta) + i \sin(\theta)
eiθ=cos(θ)+isin(θ)
泰勒公式(这部分作为已知不过分吧)
e
x
=
1
+
x
+
x
2
2
!
+
x
3
3
!
+
x
4
4
!
+
…
e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + \ldots
ex=1+x+2!x2+3!x3+4!x4+…
cos
x
=
1
−
x
2
2
!
+
x
4
4
!
−
x
6
6
!
+
…
\cos x = 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \ldots
cosx=1−2!x2+4!x4−6!x6+…
sin
x
=
x
−
x
3
3
!
+
x
5
5
!
−
x
7
7
!
+
…
\sin x = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \ldots
sinx=x−3!x3+5!x5−7!x7+…
欧拉公式通过正弦和余弦的求和可以近似得到,但是这个近似的公式会有符号上的问题。为了解决这个问题,我们引入虚数单位
i
i
i,从而构造了欧拉公式。

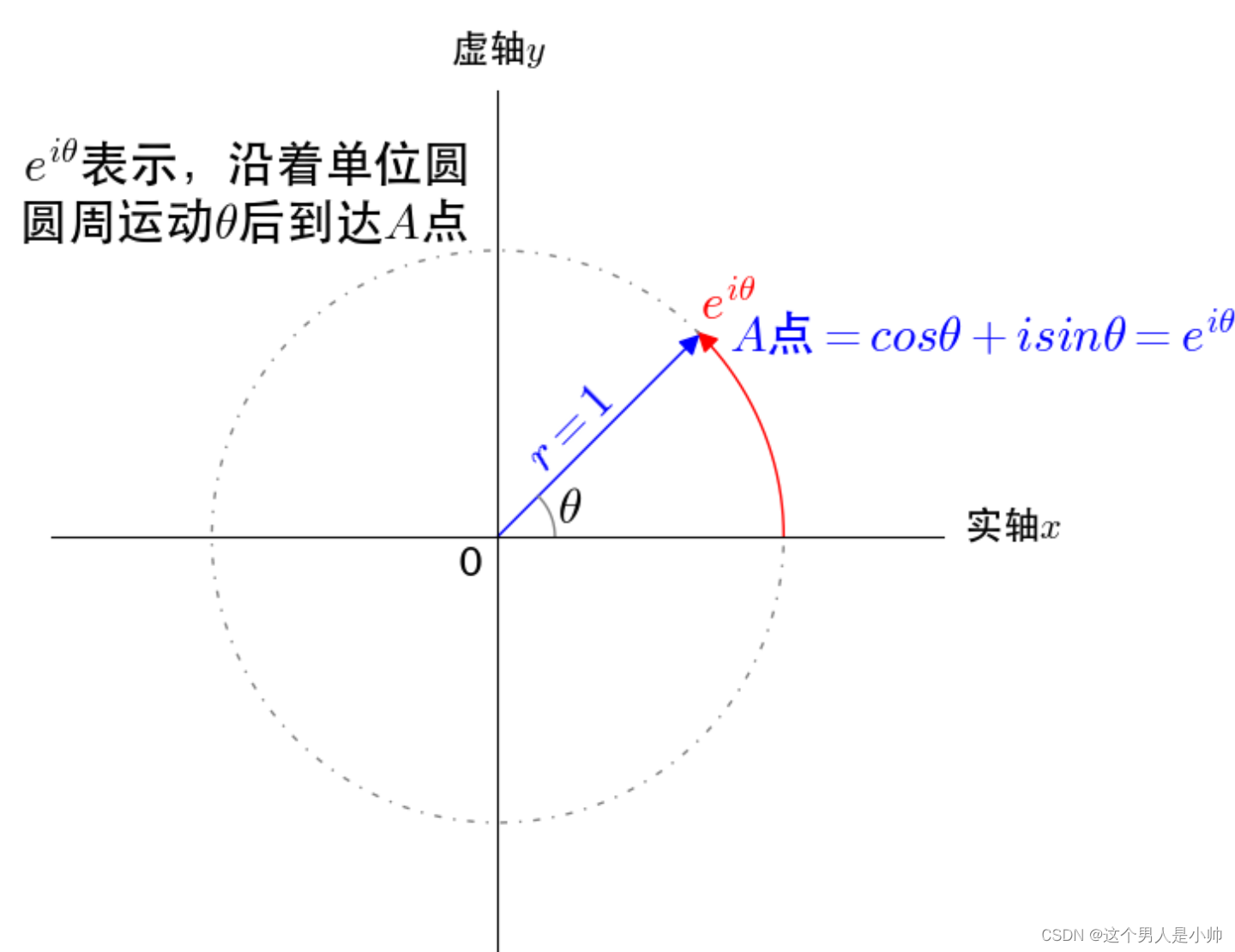
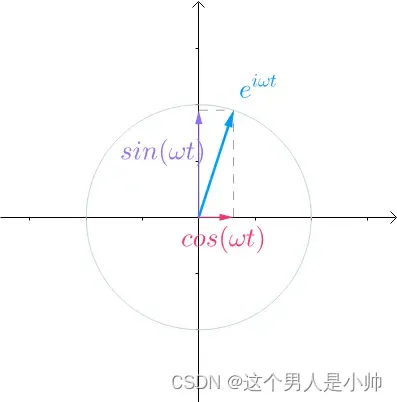
在正常的二维坐标系描述一个点使用 ( x , y ) (x,y) (x,y),在复平面上使用 ( x + i y ) (x+iy) (x+iy)。又由于半径为1所以在 x x x轴的坐标是 c o s θ cosθ cosθ,在复数轴上是 i s i n θ isinθ isinθ。所以圆周的点可以用 ( c o s θ + i s i n θ ) (cosθ+isinθ) (cosθ+isinθ)表示。
可以看到在复平面上 e i t e^{it} eit是向量所以 c o s θ , s i n θ cosθ,sinθ cosθ,sinθ也是向量
看一看到
e
i
t
e^{it}
eit是一个旋转的向量,由于欧拉公式可知,
c
o
s
(
w
t
)
和
s
i
n
(
w
t
)
也是向量
cos(wt)和sin(wt)也是向量
cos(wt)和sin(wt)也是向量
这种向量被称为函数向量。
T
T
T是
f
(
x
)
,
g
(
x
)
f(x),g(x)
f(x),g(x)的周期。对函数向量进行内积如下
⟨
f
,
g
⟩
=
∫
0
T
f
(
x
)
g
(
x
)
d
x
\langle f, g \rangle = \int_{0}^{T} f(x)g(x) \,dx
⟨f,g⟩=∫0Tf(x)g(x)dx
要计算
∫
0
2
π
sin
(
x
)
cos
(
x
)
d
x
\int_{0}^{2\pi} \sin(x) \cos(x) \, dx
∫02πsin(x)cos(x)dx可以利用三角恒等式
sin
(
2
x
)
=
2
sin
(
x
)
cos
(
x
)
\sin(2x) = 2\sin(x)\cos(x)
sin(2x)=2sin(x)cos(x)来简化。将乘积积分转化为对
s
i
n
(
2
x
)
sin(2x)
sin(2x) 的积分:
∫ 0 2 π sin ( x ) cos ( x ) d x = 1 2 ∫ 0 2 π sin ( 2 x ) d x = 0 \int_{0}^{2\pi} \sin(x) \cos(x) \, dx = \frac{1}{2} \int_{0}^{2\pi} \sin(2x) \, dx =0 ∫02πsin(x)cos(x)dx=21∫02πsin(2x)dx=0
由于 sin ( 2 x ) \sin(2x) sin(2x) 在 [ 0 , 2 π ] [0, 2\pi] [0,2π] 上是一个完整的周期,因此在该区间上的积分为零。换句话说,该函数在这个区间上的函数向量正交内积为0。它们的加权求和得到的也是函数向量。
回到最初的问题。
如果f(t) sinx cosx是向量,并且 sinx cosx是一组正交基的话是不是就好求了 。
就是上面
m
m
m,
n
n
n的计算方式得到的:
或者:
故通过这种方式求得
上半部分说的是周期函数,那么非周期函数呢?理解成非周期函数是一个周期很大的周期函数:
最终得到了傅立叶变换的公式
这部分用x来表示时间和下面的公式t是一样的东西只是表述不同,别纠结
换成这种形式如何理解这个公式呢?
f
(
x
)
=
1
2
π
∫
−
∞
∞
F
(
w
)
⋅
e
i
w
x
d
w
f(x) = \frac{1}{2\pi} \int_{-\infty}^{\infty} F(w) \cdot e^{iwx} \,dw
f(x)=2π1∫−∞∞F(w)⋅eiwxdw
称第一个
f
(
x
)
f(x)
f(x)是傅立叶逆变换。就是傅立叶级数转换过来的公式。
F
(
w
)
=
∫
−
∞
∞
f
(
x
)
⋅
e
−
i
w
x
x
F(w) = \int_{-\infty}^{\infty} f(x) \cdot e^{-iwx} \,x
F(w)=∫−∞∞f(x)⋅e−iwxx
称第二个 F ( w ) F(w) F(w)是傅立叶变换。就是傅立叶级数中用来求权重的公式。
3.2.3 对于时域到频域的理解
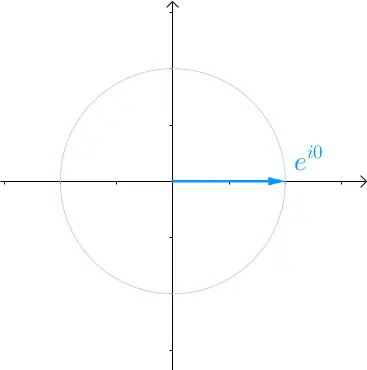
前面再介绍复平面时候把
θ
θ
θ成为角度一个常数,当他作为代表时间变量t的时候就是:
e
i
θ
=
e
i
t
e^{i\theta}=e^{it}
eiθ=eit
随着时间
t
t
t的流逝,从0开始增长这个向量随之旋转,
2
π
2\pi
2π秒会转一圈,周期
T
T
T为
2
π
2\pi
2π:
通过三角函数表示
e
i
t
e^{it}
eit
通过欧拉公式来记录下时间
t
t
t轴上的虚部也就是纵坐标记录下来,得到
s
i
n
(
t
)
sin(t)
sin(t)
e
i
t
=
cos
(
t
)
+
i
sin
(
t
)
e^{it} = \cos(t) + i \sin(t)
eit=cos(t)+isin(t)
用符号表示为
s
i
n
(
t
)
=
I
m
(
e
i
t
)
sin(t)=Im(e^{it})
sin(t)=Im(eit)
同理需要表示
s
i
n
(
2
t
)
=
I
m
(
e
i
2
t
)
sin(2t)=Im(e^{i2t})
sin(2t)=Im(ei2t)
如果要是把时间
t
t
t轴上的实部也就是横坐标记录下来,得到
c
o
s
(
t
)
cos(t)
cos(t)
用符号表示为
c
o
s
(
t
)
=
R
e
(
e
i
t
)
cos(t)=Re(e^{it})
cos(t)=Re(eit)
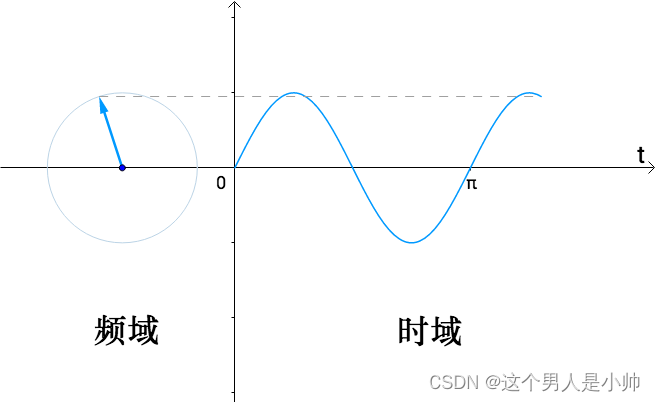
我们称旋转的这个区域为频域,
w
w
w也就是旋转的频率,得到的时间轴上的区域为时域:
为了更容易理解,简单来说,对于一个函数
f
(
x
)
f(x)
f(x),进行傅立叶变换时,我们将其乘以一个正交基,这样就会得到对这个基的拉伸幅度。这实际上等同于将其在频域中对应向量进行了同等幅度的拉伸。在频域中绘制圆等同于在时域中绘制正弦波曲线,因此,当
f
(
x
)
f(x)
f(x) 乘以正交基时,我们得到了对当前正弦波的振幅拉伸情况,这相当于频域中旋转的那个向进行了同等幅的拉伸。因此,这两个域之间是可以相互转换的,这也就解释了为什么一侧是时间而另一侧是频率大小的等值公式。
举个不太恰当的例子,假设
f
(
x
)
f(x)
f(x) 是一个 (2,2) 的向量,乘以正交基 (0,1) 就得到了对当前基的拉伸情况,这实际上等同于对当前基在频域中的表现形式的也进行了相同的拉伸幅度。
这也就是为什么看到傅立叶变换就是时域转到频域进行操作。
F
(
w
)
=
∫
−
∞
∞
f
(
t
)
⋅
e
−
i
w
t
t
F(w) = \int_{-\infty}^{\infty} f(t) \cdot e^{-iwt} \,t
F(w)=∫−∞∞f(t)⋅e−iwtt
同理得到了这个拉伸情况,乘上不同的正交基,就得到了原来的函数。
f
(
t
)
=
1
2
π
∫
−
∞
∞
F
(
w
)
⋅
e
i
w
t
d
w
f(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} F(w) \cdot e^{iwt} \,dw
f(t)=2π1∫−∞∞F(w)⋅eiwtdw
时域和频域,就是空间转换。通过频域表示时域。
类似于这个图在时域上的cos的振幅大小,等于拉伸频域的向量的幅度。
w
w
w就是对应拉伸了时域中的哪个(正弦波)三角函数。所以会说将时域问题转换到频域进行处理,计算得到了在时域的拉伸情况,从而得到不同频率的权重。就是频域中不同向量需要拉伸的幅度。
F
(
w
)
=
∫
−
∞
∞
f
(
t
)
⋅
e
−
i
w
t
t
F(w) = \int_{-\infty}^{\infty} f(t) \cdot e^{-iwt} \,t
F(w)=∫−∞∞f(t)⋅e−iwtt
3.2.4 拉普拉斯矩阵
****************************************************************************************重要的部分来了
因此,我们知道了实现傅立叶变换的基本条件,正交基。频率。
为了实现在图上的傅立叶要找到这组正交基和频率
拉普拉斯矩阵的目的就是找到正交基和频率
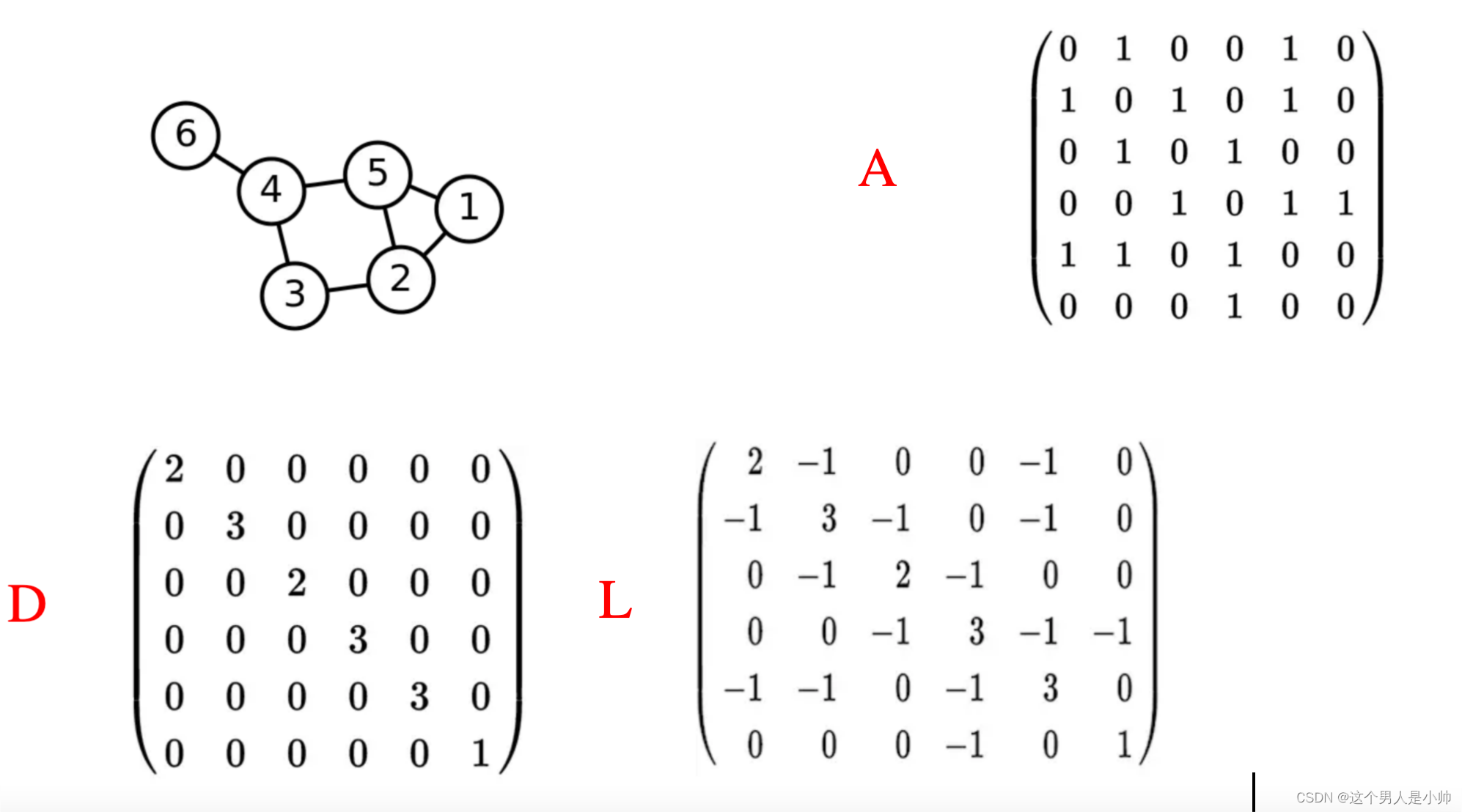
图结构的信息能得到的就是只有图的邻接矩阵
A
A
A度矩阵
D
D
D。通过度矩阵和邻接矩阵相减构构造拉普拉斯矩阵:
构造的矩阵具有出色的性质:它是对称半正定矩阵,其所有特征值均为非负数。这种性质意味着矩阵可以实现相似对角化,也称为特征分解。
L
=
U
Λ
U
−
1
L = U \Lambda U^{-1}
L=UΛU−1
其中:
- U U U 是正交矩阵,其列是 L L L 的标准正交特征向量;
- Λ \Lambda Λ 是对角矩阵,其对角线上的元素是 L L L 的特征值。
这个表达式可以写成如下形式:
L = [ u 1 u 2 … u n ] [ λ 1 0 … 0 0 λ 2 … 0 ⋮ ⋮ ⋱ ⋮ 0 0 … λ n ] [ u 1 T u 2 T ⋮ u n T ] L = \begin{bmatrix} \mathbf{u}_1 & \mathbf{u}_2 & \ldots & \mathbf{u}_n \end{bmatrix} \begin{bmatrix} \lambda_1 & 0 & \ldots & 0 \\ 0 & \lambda_2 & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & \lambda_n \end{bmatrix} \begin{bmatrix} \mathbf{u}_1^T \\ \mathbf{u}_2^T \\ \vdots \\ \mathbf{u}_n^T \end{bmatrix} L=[u1u2…un] λ10⋮00λ2⋮0……⋱…00⋮λn u1Tu2T⋮unT
其中, u 1 , u 2 , … , u n \mathbf{u}_1, \mathbf{u}_2, \ldots, \mathbf{u}_n u1,u2,…,un 是拉普拉斯矩阵 L L L 对应于不同特征值的标准正交特征向量, λ 1 , λ 2 , … , λ n \lambda_1, \lambda_2, \ldots, \lambda_n λ1,λ2,…,λn 是拉普拉斯矩阵的特征值。
**由于拉普拉斯矩阵进行谱分解以后,可以得到n个线性无关的特征向量,构成空间中的一组正交基,因此归一化拉普拉斯矩阵算子的特征向量构成了图傅里叶变换的基。
找到了正交基和频率 因此可以实现图上的傅立叶变换
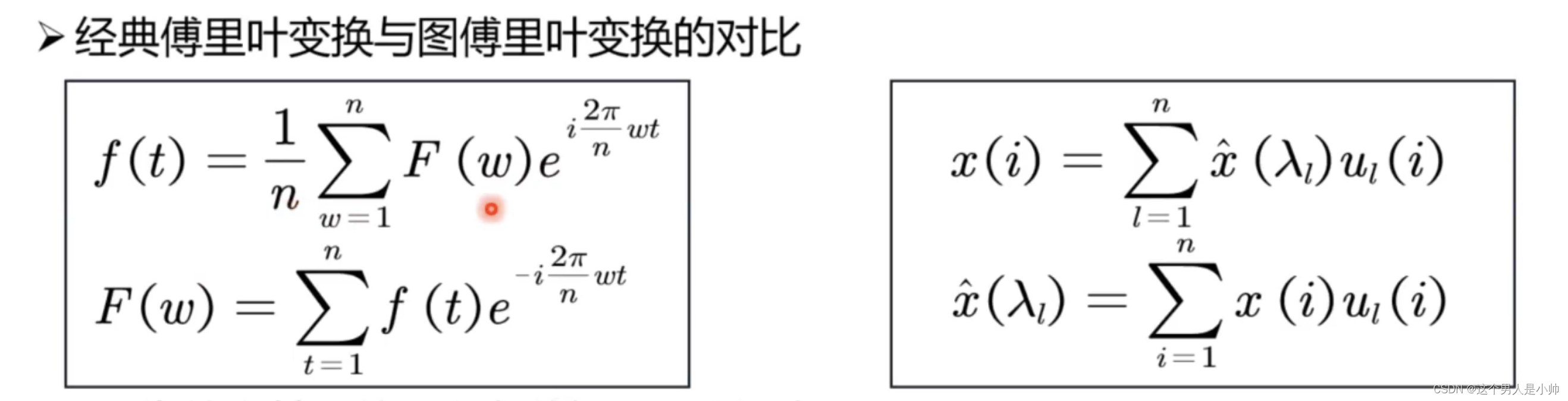
3.2.4 图傅立叶变换
傅立叶变换的输入是要进行变换的函数。在图结构中,输入是每个节点的特征向量(这个是feature不是矩阵特征向量哦),因此进行变换时需要乘以特征向量矩阵
U
U
U 的转置。会得到不同特征对不同正交基的缩放情况,等价于频域空间中的特征值进行了相同幅度的缩放,所以看成是特征值的函数形式的向量。
下面是两种形式的对比情况。
正交基描述了空域的形态,而频率则描述了频域的形态。同样地,正交特征向量
U
U
U 与输入特征
x
x
x的乘积描述了对不同特征向量的缩放情况,这等价于频域中特征值描述的空间也进行了相同的缩放。通过这样的对比,可以更容易地理解两个域之间的关系。
现在知道了如何进行图傅立叶那么图卷积就能完成了。
3.2.5 谱域图卷积
可以看到这个公式里的就是关于不同频率
w
w
w的伸缩程度,等价于时域的波动大小。
(
f
∗
g
)
=
F
−
1
(
F
(
ω
)
⋅
G
(
ω
)
)
(f * g) = F^{-1}(F(\omega) \cdot G(\omega))
(f∗g)=F−1(F(ω)⋅G(ω))
在卷积神经网络中,我们知道两个卷积的函数,一个是特征一个是卷积核,对这两部都要进行空域到频域的转换,图结构空域到频域的转换后都是都是关于特征值的函数。同理将卷积核
g
g
g进行傅立叶变换都会得到关于特征值的这种函数。所以,对输入特征进行了一次傅立叶和卷积核进行了一次傅立叶,在图傅立叶中也是一样的,最后来一次傅立叶逆变换,实现整个图卷积流程: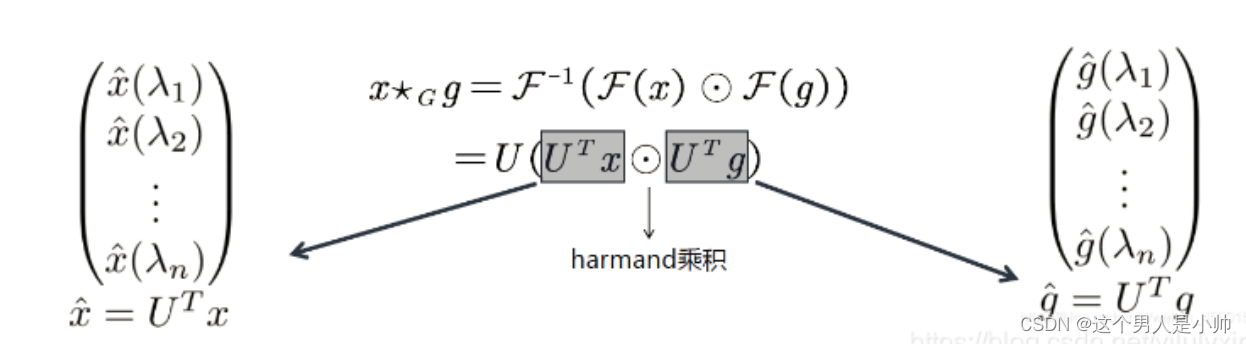
因此得到了最终的图卷积公式。