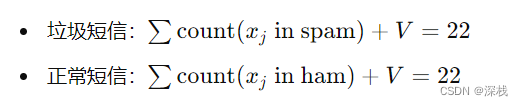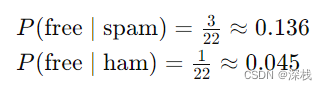贝叶斯概率公式
联合概率:包含多个条件,且多个条件同时成立的概率,例如
P
(
A
,
B
)
P(A,B)
P(A,B),即A,B同时成立的概率
条件概率:事件A在事件B发生的条件下分发生概率,记作
P
(
A
∣
B
)
P(A|B)
P(A∣B)
相互独立:如果
P
(
A
,
B
)
=
P
(
A
)
P
(
B
)
P(A,B)=P(A)P(B)
P(A,B)=P(A)P(B),则称事件A和事件B相互独立
贝叶斯公式:
P
(
C
∣
W
)
=
P
(
W
∣
C
)
P
(
C
)
P
(
W
)
P(C|W)=\frac{P(W|C)P(C)} {P(W)}
P(C∣W)=P(W)P(W∣C)P(C)
朴素贝叶斯的‘朴素’
朴素贝叶斯(Naive Bayes)算法中的“朴素”主要指的是它在假设上的简化。具体来说,这种“朴素”假设是指在进行分类时,各个特征之间是相互独立的。也就是说,给定类别的情况下,一个特征的存在或不存在与其他特征是独立的。
虽然说这种假设往往并不成立,因为特征之间通常存在一定的相关性。然而这种朴素的假设大大简化了计算,使得贝叶斯分类器在计算效率上具有很大的优势,同时在很多实际应用中依然能够提供较好的分类效果。尽管它的假设较为简化,但朴素贝叶斯算法在文本分类、垃圾邮件过滤等领域表现出色。
垃圾短信分类实例
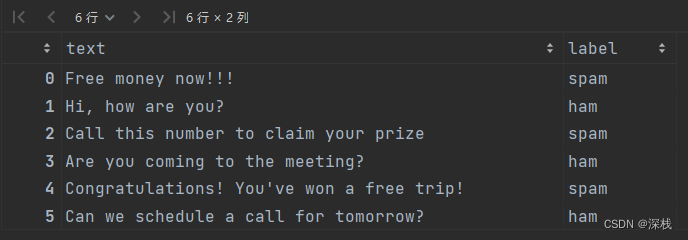
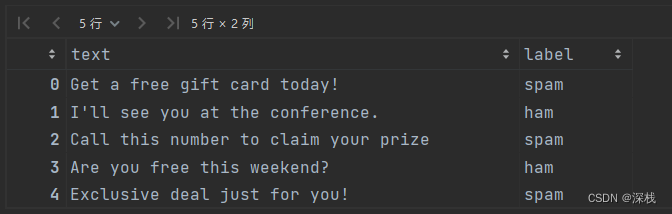
现在有6条短信,如下所示
标签spam表示是垃圾信息,ham表示是正常信息
贝叶斯公式
P
(
C
∣
W
)
=
P
(
W
∣
C
)
P
(
C
)
P
(
W
)
P(C|W)=\frac{P(W|C)P(C)} {P(W)}
P(C∣W)=P(W)P(W∣C)P(C)
1、计算先验概率
P
(
C
)
P(C)
P(C)(C表示类别)
P
(
s
p
a
m
)
=
3
6
=
0.5
P(spam)=\frac{3}{6}=0.5
P(spam)=63=0.5
P
(
h
a
m
)
=
3
6
=
0.5
P(ham)=\frac{3}{6}=0.5
P(ham)=63=0.5
2、计算似然
因为假设这些特征之间相互独立,似然
P
(
x
i
∣
C
)
P(x_i|C)
P(xi∣C)可以通过训练数据中每个单词在不同类别中的频率来估计。例如,对于单词“free”,我们可以计算它在垃圾短信和正常短信中出现的频率。
如果出现似然为0的情况如何处理?
防止出现似然为0的情况导致乘积直接为0,故引入拉普拉斯平滑系数
拉普拉斯平滑系数:
P
(
F
1
∣
C
)
=
N
i
+
α
N
+
α
m
P(F1|C)=\frac{Ni+α}{N+αm}
P(F1∣C)=N+αmNi+α ,
α
α
α为指定的系数,一般为1,m为训练文档中特征词种类个数
若加入拉普拉斯平滑系数,则所有的概率均需要加上对应的值。
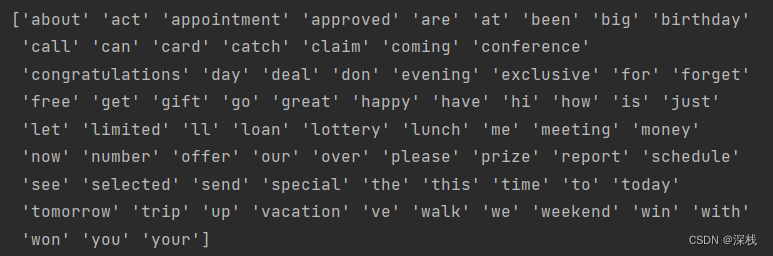
1、对上面数据集进行文本特征抽取,使用sklearn提供的CountVectorizer即可,将文本转小写,去除标点符号,进行分词,去除停用词,词形还原等。
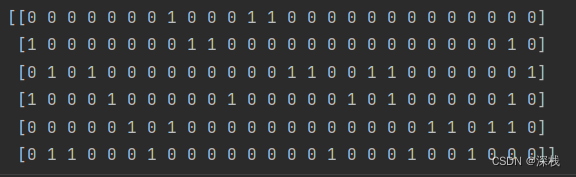
分割后的特征词如下:
对应词频矩阵如下:
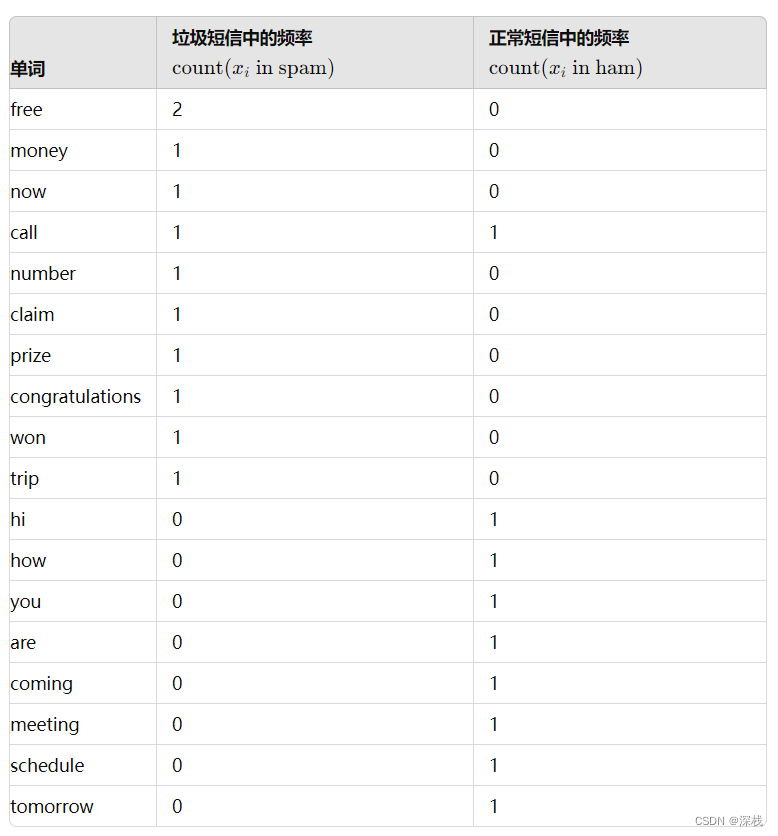
接下来进行词频统计:
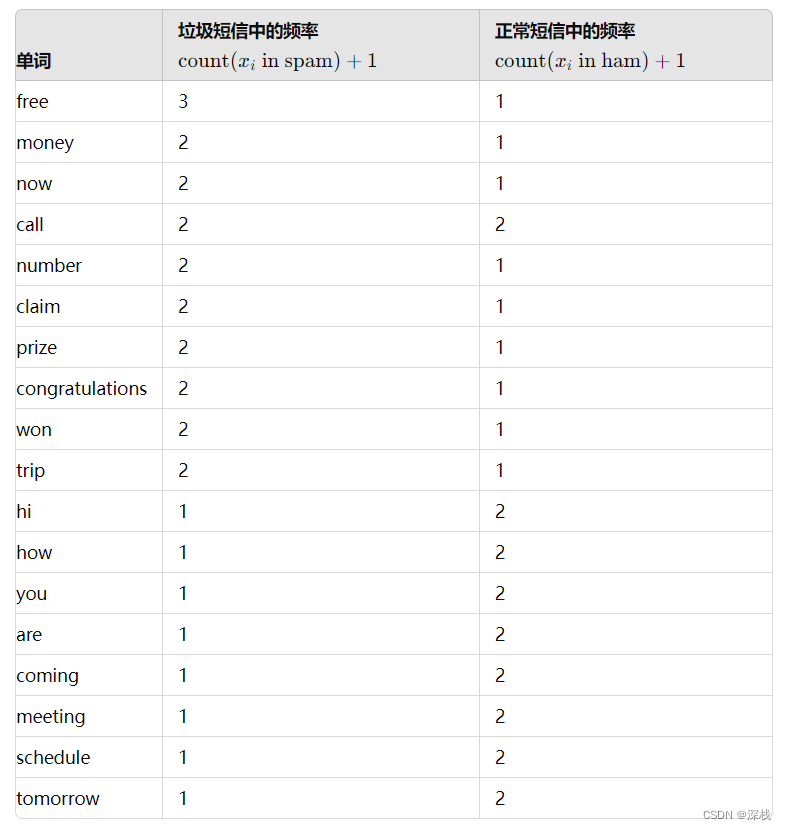
加上拉普拉斯平滑系数(每个词频加1)
计算每个类别中的总单词数(包括平滑)
以free为例,似然计算为:
设待测试短信为:Free call now!
则计算
P
(
s
p
a
m
∣
f
r
e
e
c
a
l
l
n
o
w
)
=
P
(
s
p
a
m
)
×
P
(
f
r
e
e
∣
s
p
a
m
)
×
P
(
c
a
l
l
∣
s
p
a
m
)
×
P
(
n
o
w
∣
s
p
a
m
)
P(spam|free call now)=P(spam)×P(free|spam)×P(call|spam)×P(now|spam)
P(spam∣freecallnow)=P(spam)×P(free∣spam)×P(call∣spam)×P(now∣spam)
=
0.5
×
3
22
2
22
2
22
=0.5×\frac{3}{22}\frac{2}{22}\frac{2}{22}
=0.5×223222222
≈
0.00055
≈0.00055
≈0.00055
再计算:
P
(
h
a
m
∣
f
r
e
e
c
a
l
l
n
o
w
)
=
P
(
h
a
m
)
×
P
(
f
r
e
e
∣
h
a
m
)
×
P
(
c
a
l
l
∣
h
a
m
)
×
P
(
n
o
w
∣
h
a
m
)
P(ham|free call now)=P(ham)×P(free|ham)×P(call|ham)×P(now|ham)
P(ham∣freecallnow)=P(ham)×P(free∣ham)×P(call∣ham)×P(now∣ham)
=
0.5
×
1
22
2
22
1
22
=0.5×\frac{1}{22}\frac{2}{22}\frac{1}{22}
=0.5×221222221
≈
0.00001
≈0.00001
≈0.00001
比较大小:
P
(
s
p
a
m
∣
f
r
e
e
c
a
l
l
n
o
w
)
比
P
(
h
a
m
∣
f
r
e
e
c
a
l
l
n
o
w
)
P(spam|free call now)比P(ham|free call now)
P(spam∣freecallnow)比P(ham∣freecallnow)大,所以此类短信分类为“
s
p
a
m
spam
spam”
朴素贝叶斯优缺点:
1)优点:对缺失数据不敏感,算法简单,易于文本分类
分类准确度高,速度快
2)缺点:由于使用了样本属性独立性假设,如果特征属性之间实际有关联,则效果不好。
API:sklearn.naive_bayes.MultinomialNB(alpha=1.0) alpha:拉普拉斯平滑系数
上述短信分类的代码如下:(数据集在文末)
import pandas as pd
data = pd.read_excel('messages.xlsx') # 该表格内有10000条信息
data.head()
# 文本特征抽取
from sklearn.feature_extraction.text import TfidfVectorizer
transfer = TfidfVectorizer()
x = transfer.fit_transform(data.text)
print(transfer.get_feature_names_out())
# 数据集划分
from sklearn.model_selection import train_test_split
x_train,x_test,y_train,y_test = train_test_split(x,data.label,train_size=0.8,random_state=2000000)
# 使用朴素贝叶斯分类
from sklearn.naive_bayes import MultinomialNB
estimator = MultinomialNB(alpha=1) # alpha为拉普拉斯平滑系数
estimator.fit(x_train,y_train)
y_predict = estimator.predict(x_test)
print(f"预测值和真实值是否相等:{y_predict==y_test}")
print(f"正确率为:{estimator.score(x_test,y_test)}")
短信数据集点击即可跳转(免费下载)