WebGL渲染3D高斯泼溅模型
原文:
GitHub - kishimisu/Gaussian-Splatting-WebGL: 3D Gaussian Splatting Renderer for WebGL
此外,一些基于webgpu,threejs渲染,以及和cesium集成的项目如下
GitHub - playcanvas/supersplat: 3D Gaussian Splat Editor GitHub -
MarcusAndreasSvensson/gaussian-splatting-webgpu
https://github.com/mkkellogg/GaussianSplats3D 🎉(很多项目基于该项目开发) GitHub -
tebben/cesium-gaussian-splatting: Test to see if we can get gaussian
splatting to work in CesiumJS (和cesium集成)
https://doc.babylonjs.com/features/featuresDeepDive/mesh/gaussianSplatting
(babylonjs渲染的官方api)
https://github.com/ebeaufay/threedtiles(以3dtiles的方式,加载3D高斯泼溅数据)
3维高斯模型基础
3维高斯函数控制形状
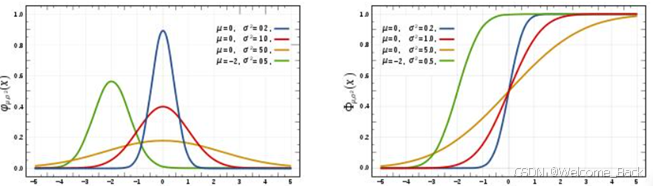
一维高斯函数,即为正态分布的曲线。形状由方差和均值控制。
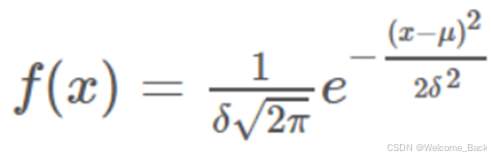
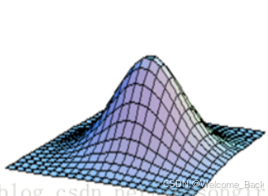
二维高斯函数,形状为一个突起面。
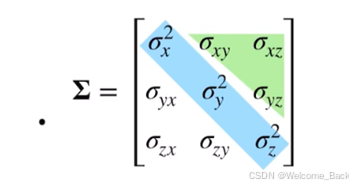
三维高斯函数,形状是一个椭球体(椭球面的积分),形状由协方差矩阵控制。旋转矩阵和缩放矩阵可以对高斯分布进行仿射变换,因此协方差矩阵可以用旋转和缩放矩阵进行表达。
3D高斯分布的协方差矩阵是一个对角矩阵。
当x y z都不相关的时候,此时椭球就是一个球。
球谐函数描述颜色
不同方向展示不同的颜色
和傅里叶级数性质类似,球谐函数也是以正交函数作为基底,傅里叶级数的正交基底为sin(nx)和cos(nx)。球谐函数则是球面上的正交基底。其主要性质有:
- 标准正交性
- 旋转不变性
- 函数乘积的积分等于其球谐系数向量的点积
坐标系变换
四个坐标系
- 世界坐标系
- 相机坐标系
- 归一化坐标系
- 像素坐标系(屏幕空间)
四种变换
观测变换(世界坐标系到相机坐标系,相机的projmatrix)
剔除在相机空间深度值小于0.4的点
投影变换(正交投影或透视投影,得到一个范围为[-1,1]的正方体,所有点都在里面,即裁切空间。方便对渲染图元进行裁切)
float p_w = 1. / (p_hom.w + 1e-7);
vec3 p_proj = p_hom.xyz * p_w; // 裁切空间的点的坐标
视口变换(将[-1,1]的标准立方体变换到[0,height],[0,width]的屏幕空间中。使用二维协方差矩阵描述)
计算二维协方差矩阵
**lambda1** **和 lambda2**:这两个变量表示协方差矩阵的两个特征值。特征值描述了高斯分布的主轴方向上的方差大小
获取my_radius,矩形区域的半径
将裁切空间坐标转换为屏幕空间坐标
计算缩放比例
计算四个顶点
光栅化
根据四个顶点绘制三角形。用四边形近似描述高斯球。
WebGL中的模型
投影矩阵用于将世界空间坐标转换为剪裁空间坐标。常用的投影矩阵(透视矩阵)用于模拟充当 3D 虚拟世界中观看者的替身的典型相机的效果。
视图矩阵负责移动场景中的对象以模拟相机位置的变化,改变观察者当前能够看到的内容。
在 WebGL 程序中,数据通常上传到具有自己的坐标系统的 GPU 上,然后顶点着色器将这些点转换到一个称为裁剪空间的特殊坐标系上。延展到裁剪空间之外的任何数据都会被剪裁并且不会被渲染。如果一个三角形超出了该空间的边界,则将其裁切成新的三角形,并且仅保留新三角形在裁剪空间中的部分。
我们需要计算出高斯体在裁切空间中的坐标(四个角点的坐标,使用矩形描述二维高斯体)
数据加载与解析
解析二进制ply文件,每个点获取62个属性数据。
提取**{ positions, opacities, colors, cov3Ds }**,分别为位置、透明度、颜色、协方差矩阵。
Position**(位置信息):椭球的中心,也是高斯分布的均值**
Covariance**(协方差矩阵):次变量可以控制椭球的大小,形状和方向**
Opacity**(不透明度):用于控制不透明度,用于Splatting****时的渲染**
Spherical harmonics**(球谐函数):球谐函数,视角相关的外观颜色**
着色器
顶点着色器处理顶点数据并输出插值变量(基于每个实例的顶点属性,按照距离线性插值。如果顶点属性都相同,那么中间区域的点的属性也相同),这些变量在光栅化过程中被插值后传递给片段着色器。
片段着色器则根据这些插值变量和其他输入(如纹理、光照参数)计算每个片段的最终颜色。
顶点着色器输出4个顶点位置和矩形的插值位置变量,交给片段着色器。片段着色器根据高斯函数,计算不同位置的颜色和透明度。
splat_vertex.glsl 用于计算点的位置
splat_fragment.glsl 用于计算点的颜色
splat_vertex.glsl顶点着色器
输入:
in vec3 a_center; //三维向量,代表点云的中心位置
in vec3 a_col; //三维向量,代表点云的颜色
in float a_opacity; //一个浮点数,代表点云的不透明度
in vec3 a_covA; //三维向量,一共6个,用两个3维描述
in vec3 a_covB;
常量:
uniform float W; //窗口宽度
uniform float H; //窗口高度
uniform float focal_x; //代表x方向的焦距
uniform float focal_y; //代表y方向的焦距
uniform float tan_fovx; //代表x方向的视场角的正切值
uniform float tan_fovy; //代表y方向的视场角的正切值
uniform float scale_modifier; //用于缩放点云的大小
uniform mat4 projmatrix; //用于投影变换
uniform mat4 viewmatrix; //用于视图变换
输出:
// 在片段着色器中作为输入的变量
out vec3 col; // 颜色
out float depth; // 深度值
out float scale_modif; // 缩放因子
out vec4 con_o; // 协方差矩阵 + 不透明度
out vec2 xy; // 传递给片段着色器的点在屏幕空间中的位置
out vec2 pixf; // 传递给片段着色器的顶点在屏幕空间中的位置
计算步骤
第一步:观测变换+投影变换
l 世界坐标系 转换为 相机坐标系
l 相机坐标系 转换为 裁切空间坐标系
第二步:剔除距离相机过近的点
l 原始坐标系乘视图矩阵,坐标z值即为到相机的距离。小于0.4移除
第三步:计算二维协方差矩阵,获取二维高斯分布在屏幕空间的扩展范围
根据三维协方差矩阵、相机焦距、fov、视图矩阵,计算二维协方差矩阵。
cov.x 表示协方差矩阵的 [0][0] 元素(即 x 方向的方差)。
cov.y 表示协方差矩阵的 [0][1] 元素(即 x 和 y 方向的相关性)。
cov.z 表示协方差矩阵的 [1][1] 元素(即 y 方向的方差)。
计算二维协方差矩阵的逆
计算高斯分布的长轴长度和短轴长度
计算高斯分布的半径,即3倍长轴
计算高斯分布中心点的屏幕坐标
第三步:计算矩形的四个角点
vec2 screen_pos = point_image + my_radius * corner;
my_radius是矩形的边长(经过缩放后)
corner为 [-1,-1],[1,-1],[-1,1],[1,1]
point_image是矩形的中心点
每个矩形为二维高斯分布的扩展范围,可以覆盖99.7%的点。
splat_fragment.glsl片元着色器
输入:
in vec3 col; //三维向量,代表片段的颜色
in float scale_modif; //缩放高斯点云的大小
in float depth; //代表片段的深度值
in vec4 con_o; //四维向量,包含二维高斯分布的协方差矩阵信息
in vec2 xy; //二维向量,代表片段在图像坐标系中的位置
in vec2 pixf; //二维向量,矩形四个顶点的位置
输出:
out vec4 fragColor; //四维向量,表示片段的颜色和透明度
第一步:计算顶点和中心位置的偏移
vec2 d = xy - pixf;
计算三维高斯函数的指数项
float power = -0.5 * (con_o.x * d.x * d.x + con_o.z * d.y * d.y) - con_o.y * d.x * d.y;
注意:power值是负的,power越小,距离中心越近。大于0的舍弃
即所绘制片段距离中心的距离
第二步:计算透明度
float alpha = min(.99f, con_o.w * exp(power));
大于0.9就默认为0.9,小于0.9,则计算透明度。
Power越小,exp(power)越大,alpha越大。即越远越透明。
第三步:丢弃透明度小的片段,绘制出椭圆
由float power = -0.5 * (con_o.x * d.x * d.x + con_o.z * d.y * d.y) - con_o.y * d.x * d.y;
float alpha = min(.99f, con_o.w * exp(power));
if (alpha < 1./255.) {
discard;
}
第四步:设置透明度,实现颜色过渡效果
fragColor = vec4(color, alpha);