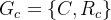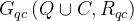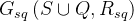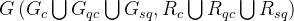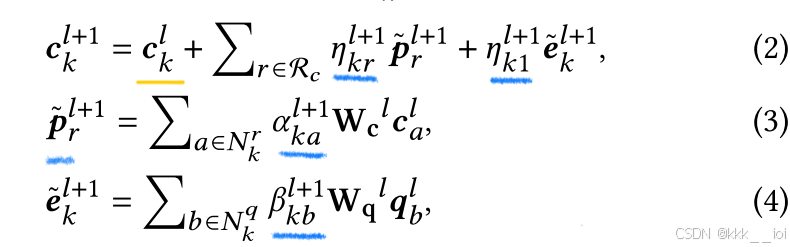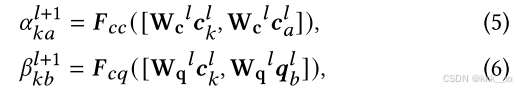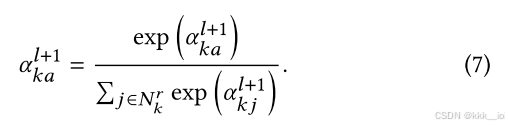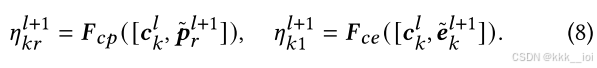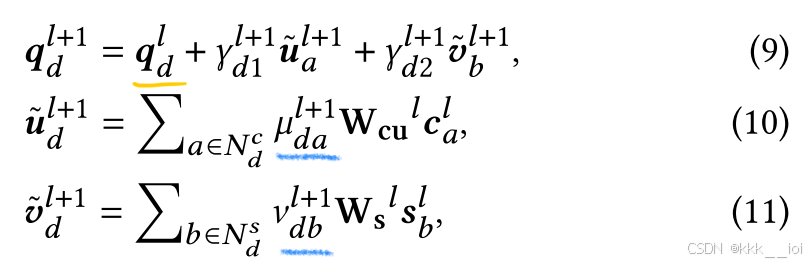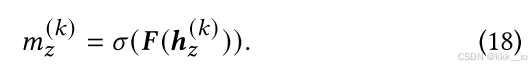文章链接🔗RCD: Relation Map Driven Cognitive Diagnosis for Intelligent Education Systems
目录
3.4.3 Extendable Diagnosis Layer (可扩展的诊断层)
1. Motivation(针对的问题)
现有方法的局限性:
- 层间交互建模:传统方法(如 IRT 和 DINA)专注于学生-题目或学生-知识点之间的交互,忽略了知识点内部的结构化关系(如先后学习顺序、依赖关系)。
- 缺乏层次化建模:学生-题目-知识点之间的多层次关系未被全面建模,导致信息利用不足。
2. Method (解决方案)
-
多层关系图建模:
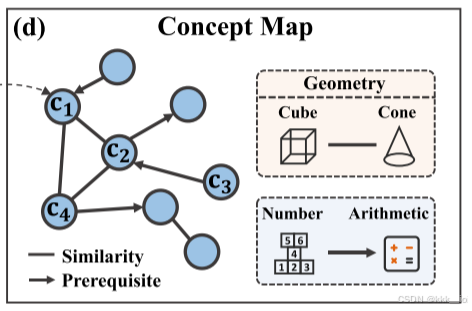
将学生、题目和知识点表示为不同层次的节点,并构建三个局部关系图:- 知识点依赖图:描述知识点之间的关系(如先后学习顺序或关联性)。
- 知识点-题目关联图:是一个二部图,描述题目涉及的知识点。
- 学生-题目交互图:学生与题目的答题交互情况,例如答题正确率。
- 知识点依赖图:描述知识点之间的关系(如先后学习顺序或关联性)。
-
多层注意力网络:
利用注意力机制,分别聚合每个局部图内部的节点关系,并跨关系图聚合不同层次的关系。 -
可扩展诊断函数:
通过联合训练网络,设计一个扩展性强的预测函数,既能预测学生表现,又能学习关系感知的节点表示。
3. RCD Implement 实现
3.1 符号定义
- 三个局部图
- 知识点依赖图(Concept Dependency Map):
表示知识点concept的集合;
从是多个教育关系组成的集合,
表示某一特定的概念类型,例如先序关系、相似关系;
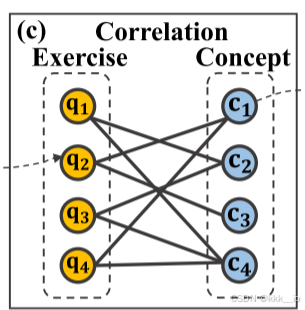
- 习题-知识点关联图(Exercise-concept Correlation Map):
表示习题的集合;
是概念的集合;
指的是习题和概念之间的关系,如
表示习题
中 包含概念
;
- 学生-习题图(Student-Exercise Interaction Map):
表示学生的集合;
是习题的集合;
指的是学生和习题之间的交互关系,如
表示x学生
回答了习题
(注意这里是是否回答而不是是否正确回答)
- 知识点依赖图(Concept Dependency Map):
- RCD中总的关系图:
3.2 Probelm Statement 问题定义
- N Students:
- M Exercises:
- K Konwledge concepts:
- 习题-知识点的关系集合 :
- 学生的回答记录:
由此得到了一个三元组(s,q,

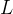
3.3 RCD Framework 模型框架
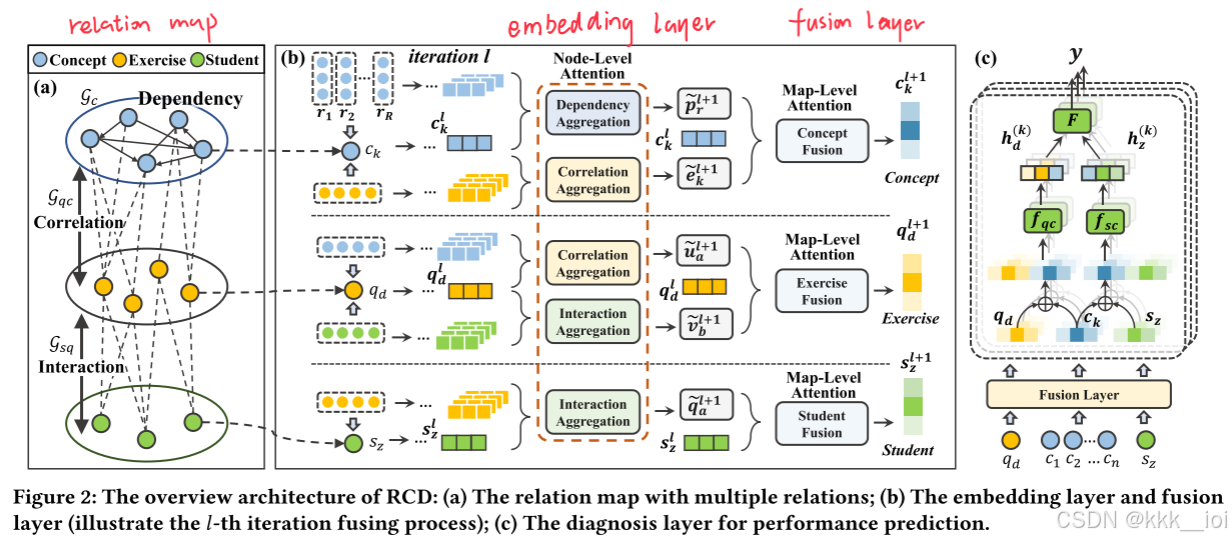
总体来看,模型由三层实现:首先由 ①嵌入层(Embedding Layer) 得到学生s,习题q,概念c的向量表示;然后由②融合层(Fusion Layer)在每个局部关系图中通过节点级和图级的注意力机制聚合邻居节点的信息迭代地得到(迭代次数L?)s、q、c的融合表示;最后在③诊断层(Diagnosis Layer)设计交互函数预测学生表现。
3.4 Implement Details 实现细节
3.4.1 Embedding Layer(嵌入层)
在嵌入层,分别通过三个可学习的矩阵将学生s、习题q和知识点c的独热编码映射为一个嵌入向量(上标0可以看作是首次迭代之前的原始向量):
3.4.2 Fusion Layer (融合层)
- Knowledge Concept Fusion 知识点融合
知识点向量q受到两个图的影响: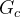
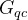
在图 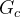
在图 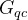
因此,用 表示在关系

表示包含知识点
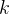
轮的迭代中,第k个知识点的嵌入受到第上一轮的知识点嵌入
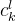
和
的影响:
在公式(3)中,其中 指的是在图
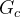
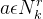
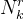
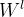
在公式(4)中,其中 指的是在图
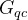
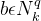
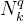
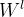
和
这两个注意力权重是节点级的,而公式(2)中的两个权重
和
是图级的注意力权重,用于平衡两个图的贡献程度。为了建模这种多层的结构,文章建模了一个多层注意力网络来计算注意力权重。
注:注意力权重通常由输入特征通过某种形式的比较函数生成,比如:
- 点积相似性 (Dot-product)
- 可学习的参数化函数 (Parameter-based functions)
- 带非线性激活的函数 F(⋅)
(一)node-level attention
这里的 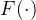
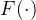
以公式(5)为例,可以理解为计算概念k :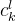
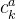
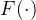
(二)map-level attention
通过节点级的注意力得到知识点依赖的聚合嵌入 和知识点-习题关联的聚合嵌入
,对于概念k:
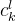
- Exercise Fusion 习题融合
习题出现在两个图中: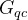
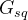
和学生-习题交互的概念嵌入
;然后基于这两个嵌入和
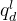

- Student Fusion 学生融合
学生是与习题直接交互的,因此与学生嵌入有关联的图只有 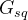
总的来书,融合层对学生-习题-知识点之间的交互关系和结构关系进行统一建模,在进行 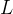
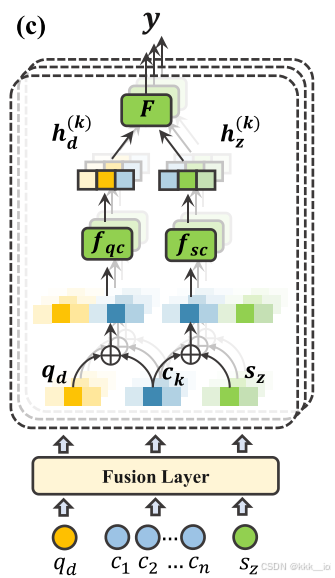
3.4.3 Extendable Diagnosis Layer (可扩展的诊断层)
诊断层基于上一层得到的学生、习题、知识点向量,预测学生表现,对于一个学生 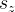
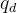
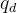
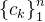


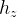
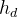
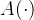
-
student factor 学生因素:
student factor描述学生的熟练程度,通过将知识点聚合向量融入学生聚合向量得到,其中 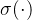
- exercise factor 习题因素:
exercise factor描述习题的难度,通过通过神经网络 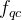
- 效用函数
:用来量化学生对练习的“优势”(如能力与难度的比较),一般实现为全连接层 F(⋅)
- 变换函数
: 将效用值转换为概率得分,用Sigmoid函数实现
- 累积函数
:将练习中涉及的所有 n 个知识点的得分进行累积,通常采用平均值。
最终的预测公式:
损失函数(交叉熵损失):
通过损失函数优化后,公式(15)得到的向量 

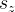
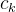

4. 模型拓展
待补充...
5. Experiments 实验
- 数据集
- junyi
- ASSIST
- 数据分布
其中 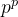
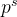
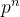
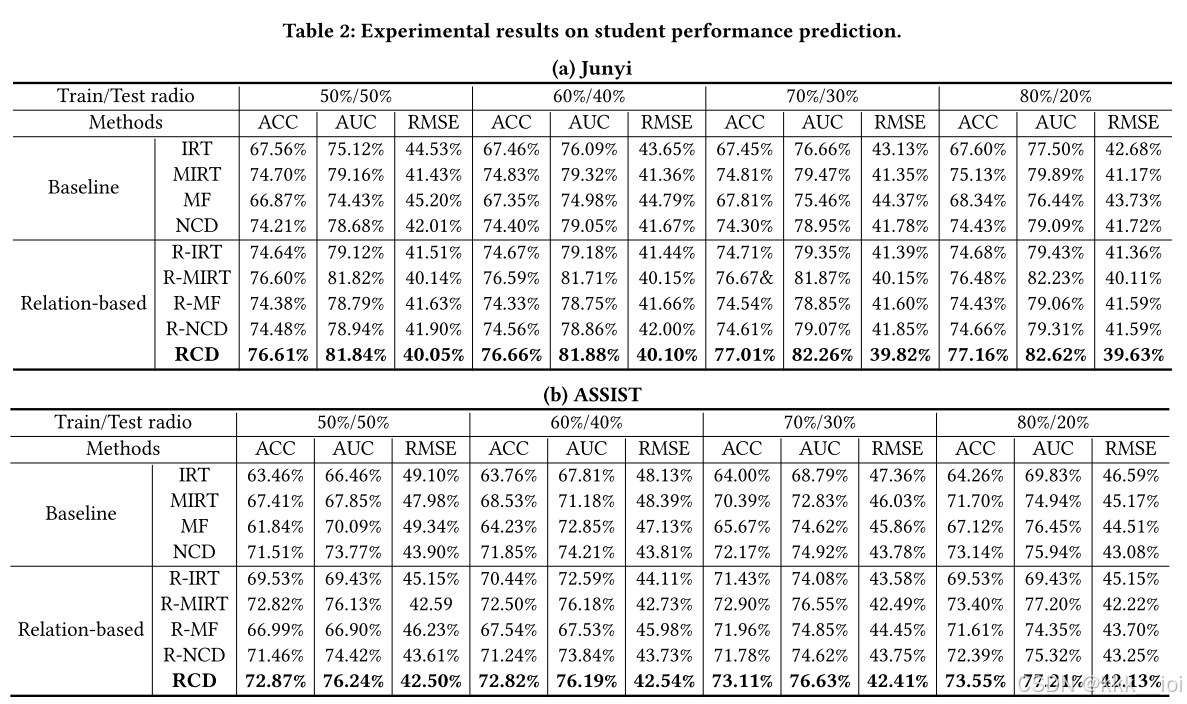
- 实验结果