已经一周没有更新我的博客了,今天浅浅的更新一下啊!
目录
1.寂寞如雪
题目分析:
这题的难点在于什么呢?
难在于求截取的一段 “寂寞” 是 它的最大的回复能量;
而这个难点牵扯到了简单的动态规划问题;动态规划我会在下一个博客写出来;
先来分析一下思路:
1.首先就是一个截取的问题;怎么截取可以使得获得的能量最大;这里设计到一个动态规划中的转移思想;
2.转移等下再说;先来分析一下如何对数据进行处理,准备一个数组,将 每一段 1 的个数 存起来;例如 :111001110001111; 数组中这样存:3 0 3 0 4 ;再对这个数组进行平方处理,偶数位赋予负值;为了方便偶数维赋予赋值 可以 在数组开头加上一个零 像这样: 0 9 0 9 0 16;这时只需要 当 i % 4 == 3 的时候乘于-1;
3.这一步就是动态规划的了;求连续区间的最大值问题;
代码实现:
#include <stdio.h>
#define maxn 1000010
#define ll long long
int min(int x, int y)
{
return x > y ? y : x;
}
int max(int x, int y)
{
return x > y ? x : y;
}
int main()
{
ll a[maxn], sum, tot, diff, ans = 0;
char ch[maxn];
scanf("%s", ch + 1);
ll len = strlen(ch + 1);
tot = ch[1] - '0';
a[tot] = tot;
//利用循环 将 1 和 0 的个数 分开
for (int i = 2; i <= len; i++)
{
if (ch[i] == ch[i - 1])
a[tot] += ch[i] - '0';
else
a[++tot] = ch[i] - '0';
}
// 平方
for (int i = 1; i <= tot; i++)
{
a[i] = a[i] * a[i];
}
diff = sum = 0;
// 偶数位取负
for (int i = 3; i <= len; i += 4)
{
a[i] = -a[i];
}
for (int i = 1; i <= len; i++)
{
if (i % 4 == 1)
diff = min(sum, diff);
sum += a[i];
ans = max(sum - diff, ans);
}
//11010111011111
// 让奇数位再取负
for (int i = 1; i <= len; i++)
{
a[i] = -a[i];
}
diff = sum = 0;
for (int i = 3; i <= len; i++)
{
if (i % 4 == 3)
diff = min(sum, diff);
sum += a[i];
ans = max(sum - diff, ans);
}
printf("%lld\n", ans);
return 0;
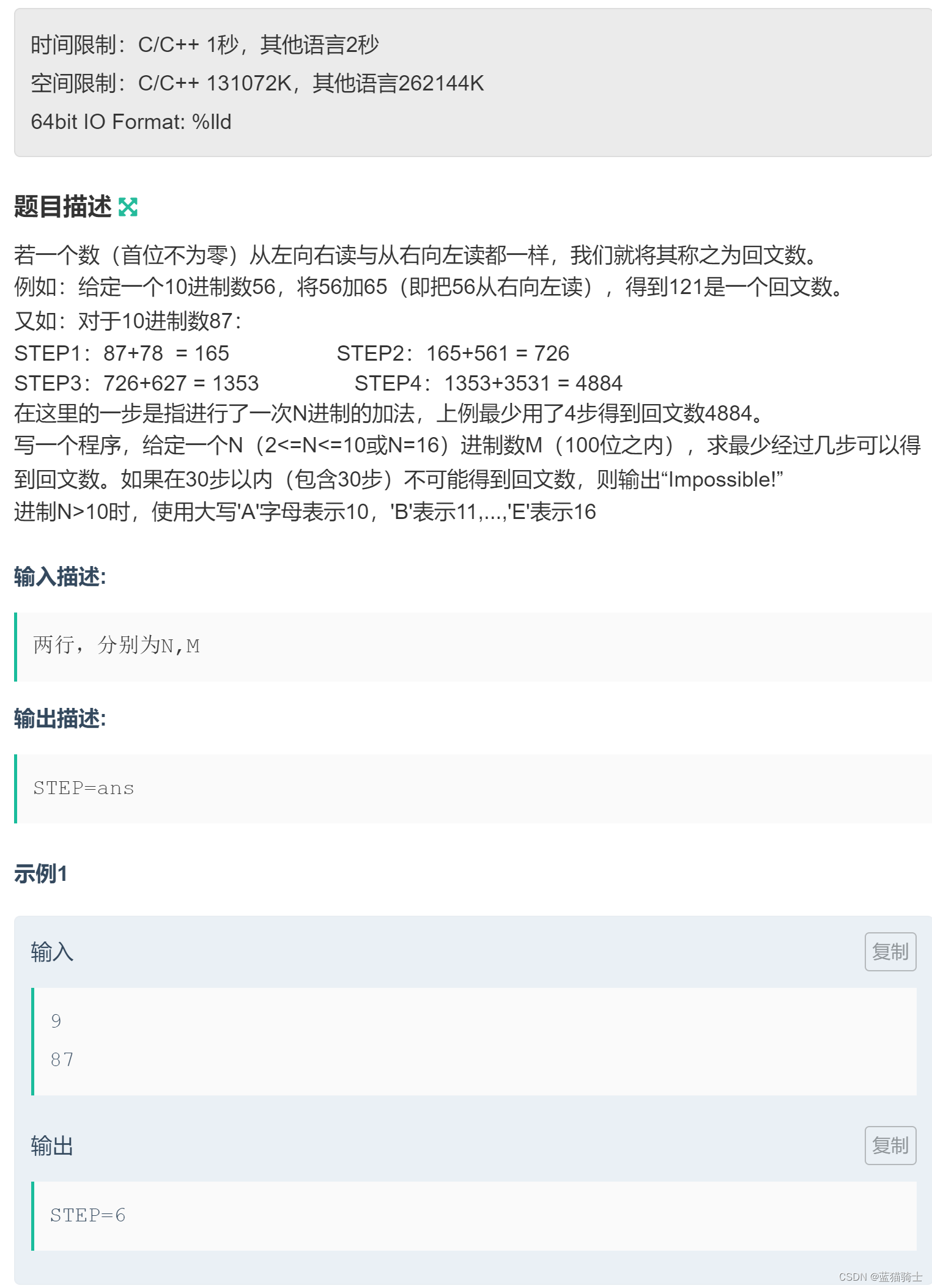
}2.[NOIP1999]回文数
题目分析:
1.这一题掺杂了进制的问题 首先它输入的数字的进制 就不一定是 10进制的;我们要把输入的数值当初字符串储存起来;
2.再准备两个数组,一个数组用来将输入的字符串转化位数值;另一个数组是储存数值的数位相加的结果;
3.对数位相加的数组进行进位处理,之后判断回文;循环就行了;
代码实现:
#include <stdio.h>
int fun(int b[], int len, int N, int flag)
{
flag++;
int i = 0;
int c[10020] = {0};
for(i=0; i<len ;i++)
{
c[i] = b[i]+b[len-1-i];
}
for(i=0; i<len ;i++)
{
if(c[i]>=N)
{
c[i+1] = c[i+1]+c[i]/N;
c[i] = c[i]%N;
}
if(c[len])
len++;
}
if(flag<=30)
{
for(i=0; i<len/2; i++)
{
if(c[i]!=c[len-i-1])
return fun(c,len,N,flag);
}
}
return flag;
}
int main()
{
int N = 0;
char a[105] = {0};
int b[105] = {0};
int flag = 0;
int i = 0;
scanf("%d", &N);
scanf("%s", a);
int len = strlen(a);
for(i=0; i<len; i++)
{
if((int)a[i]>58)
b[i] = (int)a[i]-55;
else
b[i] = (int)a[i]-48;
}
int res=fun(b, len, N, flag);
if(res<=30)
printf("STEP=%d\n", res);
else
printf("Impossible!");
return 0;
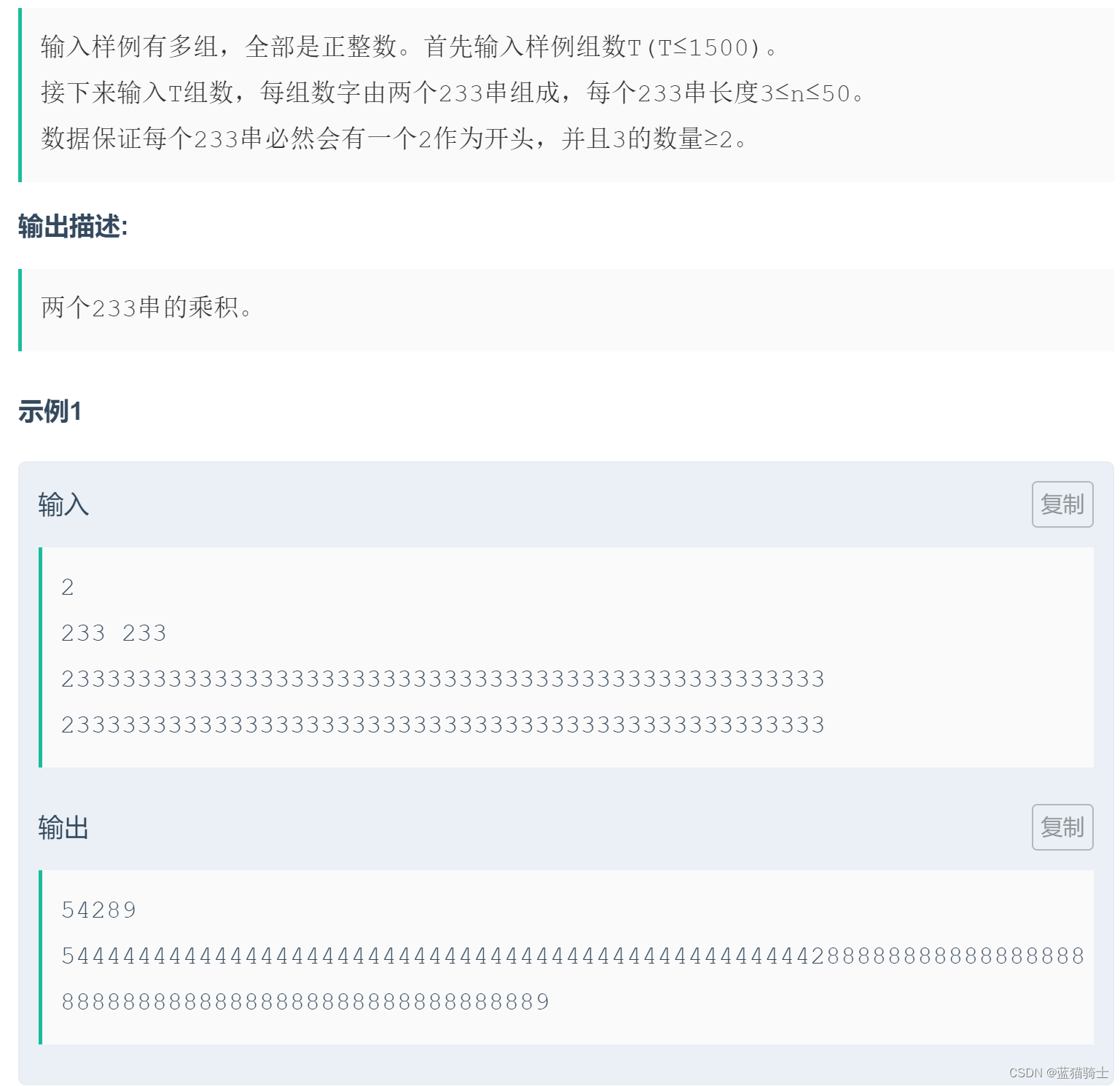
}3.高精度乘法
解法分析:
1.众所周知,乘法的运算相信大家都会;
2.我们的目的就是将这一过程用编程语言来实现;首先我们要倒置输入的数值;利用双层循环对数位进行相乘相加;然后进行进制数位的处理;
代码实现:
#include<stdio.h>
void revease(char a[], int len)
{
int i = 0;
int x = len;
for (i = 0; i < x / 2; i++)
{
char tmp = a[i];
a[i] = a[len - 1];
a[len - 1] = tmp;
len--;
}
}
int main()
{
int T = 0;
scanf("%d", &T);
while (T--)
{
char a[51] = { '0' };
char b[51] = { '0' };
scanf("%s%s", a, b);
int len1 = strlen(a);
int len2 = strlen(b);
revease(a, len1);
revease(b, len2);
int nums[1000] = { 0 };
int i = 0;
int j = 0;
for (i = 0; i < len1; i++)
{
for (j = 0; j < len2; j++)
{
nums[i + j] = nums[i + j]+(a[i] - '0') * (b[j] - '0');
}
}
for (i = 0; i < 1000; i++)
{
if (nums[i] >= 10)
{
int tmp = nums[i] / 10;
nums[i] = nums[i] % 10;
while(tmp--)
nums[i + 1]++;
}
}
int tmp = len1;
for (j = 0; j < tmp + len2 - 1 ; j++)
{
printf("%d",nums[len1 + len2 -2]);
len1--;
}
printf("\n");
}
return 0;
}