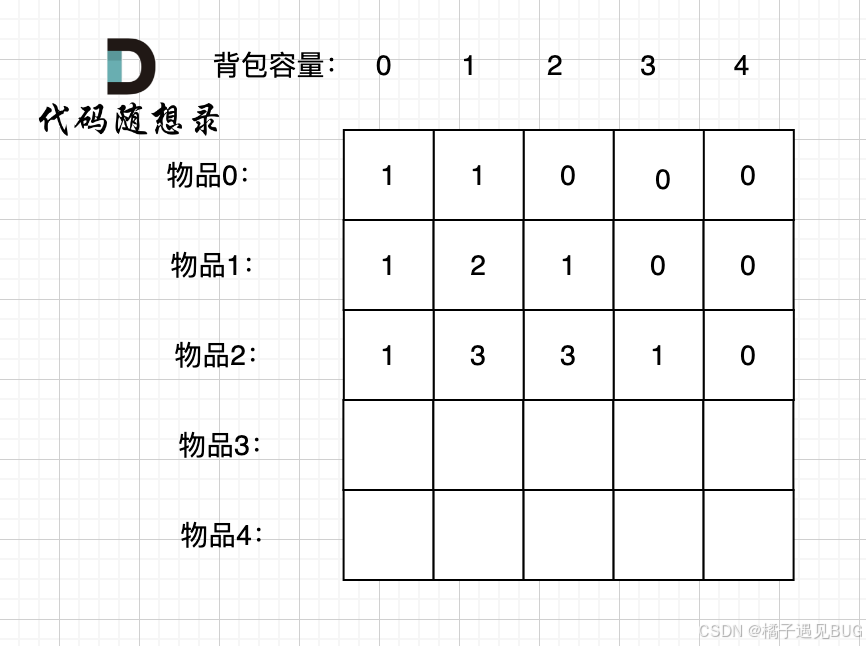
继续来看动态规划中01背包的题目。
题目:最后一块石头的重量II
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
- 如果
x == y,那么两块石头都会被完全粉碎; - 如果
x != y,那么重量为x的石头将会完全粉碎,而重量为y的石头新重量为y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
题目分析:
题目的意思就是一堆的石头相互碰撞,碰撞到最后剩下的最小重量。石头两两碰撞,需要保证剩下的部分尽可能的小,是不是就是两块石头的重量尽可能的相当,那么剩下的是不是就小了。同样的,放大到整个石堆,如果我们将石堆分成两个部分,只需要两个部分的总重量尽可能相当即可。而这个重量应该就是所有石头总重量的一半。
那么这一题就变成了尽可能的凑出这个目标重量,用01背包的视角就是,尽可能的把这个背包装满,这一点和上一题很像,上一题是求能否装满,所以两题的步骤其实大差不差。
- 确定dp数组以及下标的含义
dp[i][j]表示从0-i的石头中任取,放到容量为j的背包中,得到的做到重量(二维数组)
dp[j]表示容量(这里说容量更形象,其实就是重量)为j的背包,最多可以背最大重量为dp[j]。(一维数组)
其他的部分不必多说,和之前的没有差别,这里给出二维dp的写法和一维dp的写法,注意区别。
//二维数组
public class Solution {
public int LastStoneWeightII(int[] stones) {
int sum=0;
for(int i=0;i<stones.Length;i++){
sum+=stones[i];
}
int target=sum/2;
int[][] dp=new int[stones.Length][];//二维数组
for(int i=0;i<stones.Length;i++){
dp[i]=new int[target+1];
}
//初始化
for(int i=stones[0];i<=target;i++){
dp[0][i]=stones[0];
}
for(int i=1;i<stones.Length;i++){
for(int j=1;j<=target;j++){
if (j >= stones[i]) { //背包容量大于石头重量
//不放:dp[i - 1][j] 放:dp[i - 1][j - stones[i]] + stones[i]
dp[i][j] = Math.Max(dp[i - 1][j], dp[i - 1][j - stones[i]] + stones[i]);
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
return (sum - dp[stones.Length - 1][target]) - dp[stones.Length - 1][target];
}
}
//一维数组
public class Solution {
public int LastStoneWeightII(int[] stones) {
int sum=0;
for(int i=0;i<stones.Length;i++){
sum+=stones[i];
}
int target=sum/2;
int[] dp=new int[1501];
for(int i=0;i<stones.Length;i++){
for(int j=target;j>=stones[i];j--){
dp[j]=Math.Max(dp[j],dp[j-stones[i]]+stones[i]);
}
}
return sum - dp[target] - dp[target];
}
}题目:目标和
给你一个非负整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
- 例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3 输出:5 解释:一共有 5 种方法让最终目标和为 3 。 -1 + 1 + 1 + 1 + 1 = 3 +1 - 1 + 1 + 1 + 1 = 3 +1 + 1 - 1 + 1 + 1 = 3 +1 + 1 + 1 - 1 + 1 = 3 +1 + 1 + 1 + 1 - 1 = 3
题目分析:
因为只有+-两种符号,所以最后得到的式子一定是X-Y=target并且X+Y=sum,可以得出X=(sum+target)/2的结果,对于01背包而已,和之前的差不多,意味着我们需要凑出X这个结果。但是题目要求的是总共有多少中方式,而之前的基本都是求最大。所以这一题的递推公式有所不同。
- 确定dp数组以及下标的含义
先用 二维 dp数组求解本题,dp[i][j]:使用 下标为[0, i]的nums[i]能够凑满j(包括j)这么大容量的包,有dp[i][j]种方法。
2.确定递推公式
手动模拟
对于dp[2,2]而言有3中方式,分别是01,12,02。
那么如果不放2 呢?
dp[1,2],只有1中方式,是01
如果放2呢?
需要先将2所需的空间让出在去求,得到的是dp[1][1],2中方式,分别是只放1和只放0。
以上过程,抽象化如下:
-
不放物品i:即背包容量为j,里面不放物品i,装满有dp[i - 1][j]中方法。
-
放物品i: 即:先空出物品i的容量,背包容量为(j - 物品i容量),放满背包有 dp[i - 1][j - 物品i容量] 种方法。
本题中,物品i的容量是nums[i],价值也是nums[i]。
递推公式:dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]];
初始化
初始化部分需要考虑物品的价值为0的情况,
如果有两个物品,物品0为0, 物品1为0,装满背包容量为0的方法有几种。
- 放0件物品
- 放物品0
- 放物品1
- 放物品0 和 物品1
此时是有4种方法。其实就是算数组里有t个0,然后按照组合数量求,即 2^t 。
来看看代码,至于一维数组的解析,这里就不做了,大差不多的优化之和就行。
//二维数组
public class Solution {
public int FindTargetSumWays(int[] nums, int target) {
int sum=0;
for(int i=0;i<nums.Length;i++){
sum+=nums[i];
}
if ((target + sum) % 2 == 1) return 0; // 此时没有方案
if (Math.Abs(target) > sum) return 0; // 此时没有方案
int t=(target+sum)/2;
int[][] dp=new int[nums.Length][];
for(int i=0;i<nums.Length;i++){
dp[i]=new int[t+1];
}
if (nums[0] <= t) dp[0][nums[0]] = 1;
int numZeros=0;
for(int i=0;i<nums.Length;i++){
if(nums[i]==0) numZeros++;
dp[i][0]=(int)Math.Pow(2,numZeros);
}
for(int i=1;i<nums.Length;i++){
for(int j=1;j<=t;j++){
if(nums[i] > j) {
dp[i][j] = dp[i - 1][j];
} else {
dp[i][j] = dp[i - 1][j] + dp[i - 1][j - nums[i]];
}
}
}
return dp[nums.Length - 1][t];
}
}
//一维数组
public class Solution {
public int FindTargetSumWays(int[] nums, int target) {
int sum=0;
for(int i=0;i<nums.Length;i++){
sum+=nums[i];
}
if ((target + sum) % 2 == 1) return 0; // 此时没有方案
if (Math.Abs(target) > sum) return 0; // 此时没有方案
int t=(target+sum)/2;
int[] dp=new int[t+1];
dp[0]=1;
//遍历
for(int i=0;i<nums.Length;i++){
for(int j=t;j>=nums[i];j--){
dp[j] =dp[j]+dp[j - nums[i]];
}
}
return dp[t];
}
}题目:一和零
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
题目分析:
其实最暴力的就是分别统计每个字符串的01个数,然后去找出符合的子集,显然会超时。
那么用动态规划来解决,注意这里的每个字符只能用一次,只是01背包的问题,而非其他。至于这里的m和n其实是背包的两个维度,不好理解的话,这样,假设有一个水桶他的容量取决于高度和地面的长度,然后我们往里面放东西。
来看看dp数组
dp[i][j]:最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。注意这个方式实际上是一维数组的解法,只是因为背包有两个维度,这里写成了二维数组,如果是二维数组的写法,其实是三维数组。
dp的递推公式
dp[i][j] 可以由前一个strs里的字符串推导出来,strs里的字符串有zeroNum个0,oneNum个1。
dp[i][j] 就可以是 dp[i - zeroNum][j - oneNum] + 1。
然后我们在遍历的过程中,取dp[i][j]的最大值。
所以递推公式:dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
public class Solution {
public int FindMaxForm(string[] strs, int m, int n) {
int[,] dp = new int[m + 1, n + 1];
foreach(string str in strs){
int zero = 0, one = 0;
for(int i=0;i<str.Length;i++){
if(str[i]=='0')zero++;
else one++;
}
for (int i = m; i >= zero; i--)
{
for (int j = n; j >= one; j--)
{
dp[i, j] = Math.Max(dp[i, j], dp[i - zero, j - one] + 1);
}
}
}
return dp[m,n];
}
}那么对于二维数组的写法,实际上就上加上了关于字符数组的维度。代码部分其实差不太多
public class Solution {
public int FindMaxForm(string[] strs, int m, int n) {
int length = strs.Length;
int[,,] dp = new int[length + 1, m + 1, n + 1];
for (int i = 1; i <= length; i++) {
int[] zerosOnes = GetZerosOnes(strs[i - 1]);
int zeros = zerosOnes[0], ones = zerosOnes[1];
for (int j = 0; j <= m; j++) {
for (int k = 0; k <= n; k++) {
dp[i, j, k] = dp[i - 1, j, k];
if (j >= zeros && k >= ones) {
dp[i, j, k] = Math.Max(dp[i, j, k], dp[i - 1, j - zeros, k - ones] + 1);
}
}
}
}
return dp[length, m, n];
}
public int[] GetZerosOnes(string str) {
int[] zerosOnes = new int[2];
int length = str.Length;
for (int i = 0; i < length; i++) {
zerosOnes[str[i] - '0']++;
}
return zerosOnes;
}
}对于更详细的解析与其他语言的代码块,可以去代码随想录上查看。