四：综合练习

1.1 找出所有子集的异或总和再求和

题目链接：找出所有子集的异或总和再求和

class Solution {
    // 先定义两个全局变量，path 用于记录当前子集的异或和，sum 用于记录所有子集的异或和
    int sum, path;

    public int subsetXORSum(int[] nums){
        dfs(nums, 0);
        return sum;
    }

    /**
     * 深度优先搜索方法，生成所有子集并计算异或和
     * @param nums 输入的整数数组
     * @param pos 当前递归的位置
     */
    public void dfs(int[] nums, int pos){
        // 先让 sum 累加上当前子集的和
        sum += path;

        // 接着开始把 pos 后面的数字弄到 path 上
        for(int i = pos; i < nums.length; i++){
            path ^= nums[i]; // 获取当前子集的异或和
            dfs(nums, i + 1); // 递归处理 i 后面的位置
            path ^= nums[i]; // 回溯，用异或消消乐把最后一个元素弄掉
        }
    }
}

1.2 全排列 II

题目链接：全排列 II

class Solution {
    // 先定义三个全局变量， path 用于记录当前路径，ret 用于存储最终结果， check 用于记录某个元素是否被使用
    List<Integer> path;
    List<List<Integer>> ret;
    boolean[] check;

    public List<List<Integer>> permuteUnique(int[] nums){
        // 先初始化三个全局变量
        path = new ArrayList<>();
        ret = new ArrayList<>();
        check = new boolean[nums.length];


        Arrays.sort(nums); // 排序一下数组，为剪枝做准备
        dfs(nums, 0);
        return ret;
    }

    /**
     * 深度优先搜索方法，生成所有不重复排列
     * @param nums 输入的整数数组
     * @param pos 当前递归的深度
     */
    public void dfs(int[] nums, int pos){
        // 如果当前路径的长度到达了数组的长度，说明排列已经弄好了，返回即可
        if(path.size() == nums.length){
            ret.add(new ArrayList(path));
            return;
        }

        // 接下来就遍历一下数组的每一个元素，直到 path 的个数等于数字的长度为止
        for(int i = 0; i < nums.length; i++){

            // 剪枝条件，确保不重复：
            // 1. 当前元素未被使用 (check[i] == false)
            // 2. 如果当前元素与前一个元素相同 (nums[i] == nums[i - 1])，
            //    则前一个元素必须已经被使用 (check[i - 1] == true)
            if (check[i] == false && (i == 0 || nums[i] != nums[i - 1] || check[i - 1] != false)){
                path.add(nums[i]);
                check[i] = true;

                dfs(nums, i + 1);

                path.remove(path.size() - 1); // 回溯
                check[i] = false; 
            }

        }
        
    }
}

1.3 电话号码的字母组合

题目链接：电话号码的字母组合

class Solution {
    String[] hash = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"}; // 定义哈希表，用于存储每个数字对应的字母映射
    List<String> ret;  // 全局变量 ret，用于存储所有可能的字母组合
    StringBuffer path; // 全局变量 path，用于存储当前递归路径

   
    public List<String> letterCombinations(String digits) {
        // 初始化结果列表和路径
        ret = new ArrayList<>();
        path = new StringBuffer();

        // 如果输入字符串为空，直接返回空结果
        if (digits.length() == 0) return ret;

        // 调用深度优先搜索方法，从位置 0 开始生成组合
        dfs(digits, 0);

        // 返回所有组合
        return ret;
    }

    /**
     * 深度优先搜索方法，用于生成所有字母组合
     * @param digits 输入的数字字符串
     * @param pos 当前递归的位置（处理到第几个数字）
     */
    public void dfs(String digits, int pos) {
        // 递归终止条件：如果当前位置等于输入字符串的长度
        if (pos == digits.length()) {
            ret.add(path.toString());
            return;
        }

        // 获取当前数字对应的字母字符串
        String cur = hash[digits.charAt(pos) - '0'];

        // 遍历当前数字对应的每个字母
        for (int i = 0; i < cur.length(); i++) {
            // 将当前字母加入路径
            path.append(cur.charAt(i));

            // 递归处理下一个数字
            dfs(digits, pos + 1);

            // 回溯：移除路径中最后一个字母，恢复到递归前的状态
            path.deleteCharAt(path.length() - 1);
        }
    }
}

1.4 括号生成

题目链接：括号生成

class Solution {
    // 先定义 5 个全局变量，left 用于记录左括号的个数， right 用于记录右括号的个数，n 是括号的对数，path 用于记录当前路径，ret 用于存储最终结果
    int left, right, n;
    StringBuffer path;
    List<String> ret;

    public List<String> generateParenthesis(int _n){
        // 先初始化一下全局变量
        n = _n;
        path = new StringBuffer();
        ret = new ArrayList<>();

        dfs(); // 调用 dfs 函数后直接返回结果
        return ret;
    }

    public void dfs(){
        // 递归的出口，因为我们是先添加左括号的，当右括号的数量等于 n 时，左括号的数量也一定等于 n 
        if(right == n){
            ret.add(path.toString());
            return;
        }

        // 接着就让左括号和右括号的个数都增加为 n
        if(left < n){
            path.append('('); left++;
            dfs(); // 接着继续添加 left 的个数，直到 left 的个数为 n
            path.deleteCharAt(path.length() - 1); left--; // 回溯，把最后一个括号删掉，并让 left 减减
        }

        // 要保证 right 的个数不大于 left
        if(right < left){
            path.append(')'); right++;
            dfs();
            path.deleteCharAt(path.length() - 1); right--;
        }
    }
}

1.5 组合

题目链接：组合

class Solution {
    // 先定义 4 个全局变量，path 用于记录当前路径，ret 用于存储最终结果，n 用来记录数字的个数，k 用于记录选取的数字个数
    int n, k;
    List<Integer> path;
    List<List<Integer>> ret;

    public List<List<Integer>> combine(int _n, int _k) {
        // 先初始化一下全局变量
        n = _n; k = _k;
        path = new ArrayList<>();
        ret = new ArrayList<>();

        dfs(1); // 调用 dfs 函数，从 1 开始进行深度优先遍历
        return ret;
    }

    public void dfs(int start){
        // 递归的出口
        if(path.size() == k){
            ret.add(new ArrayList<>(path));
            return;
        }

        // 把 start 后面的数字都添加到 path 中
        for(int i = start; i <= n; i++){
            path.add(i);
            dfs(i + 1);
            path.remove(path.size() - 1);
        }
    }
}

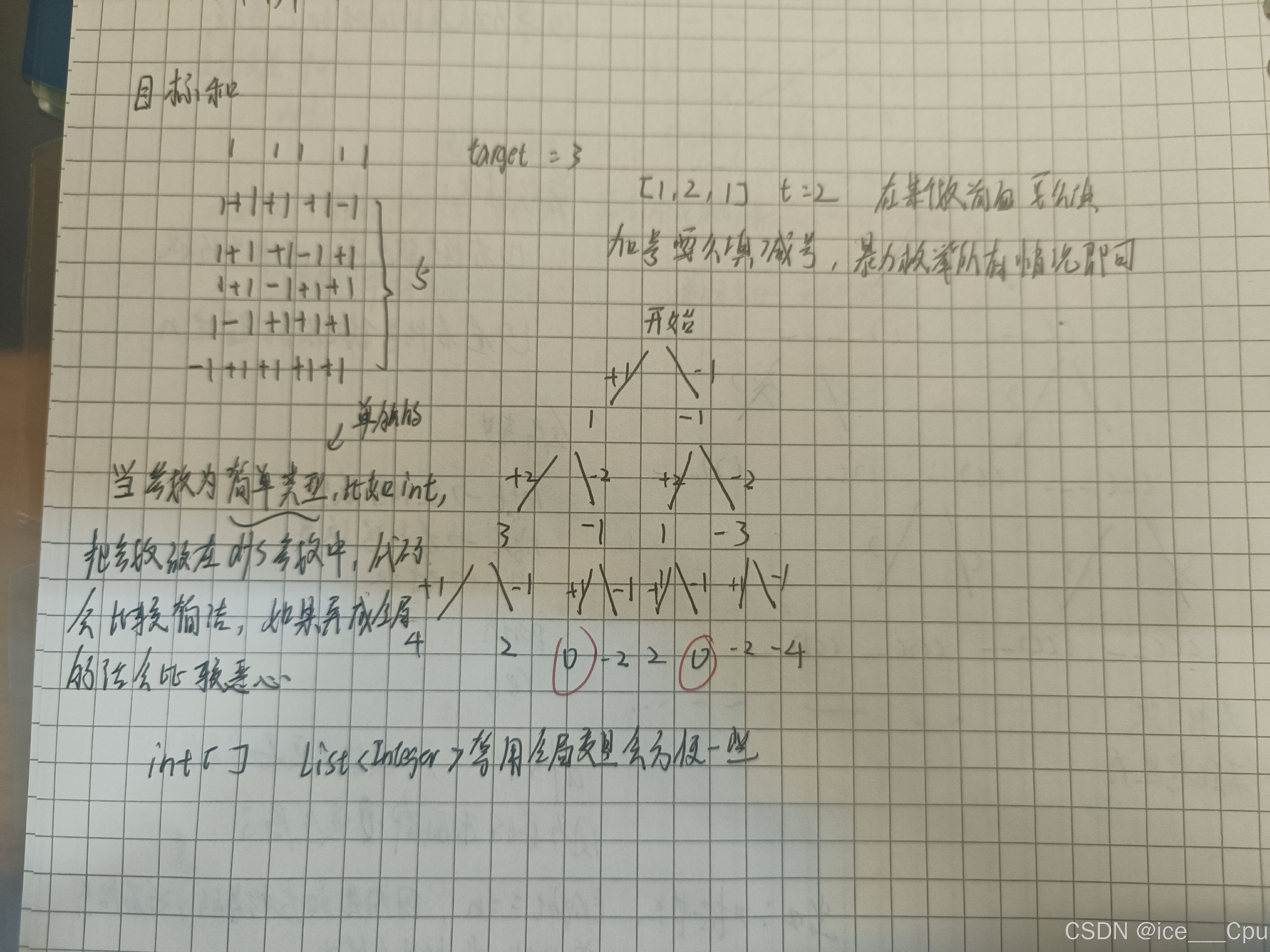
1.6 目标和

题目链接：目标和

class Solution {
    // 定义全局变量
    int ret; // 用于存储满足条件的方案数量
    int aim; // 用于存储目标值 target

    public int findTargetSumWays(int[] nums, int target) {
        // 初始化目标值
        aim = target;
        ret = 0; // 初始化满足条件的方案数量为 0
        dfs(nums, 0, 0); // 从第一个数字开始深度优先搜索，初始路径和为 0
        return ret; // 返回最终结果
    }

    public void dfs(int[] nums, int pos, int path) {
        // 递归出口：当遍历到数组的末尾时
        if (pos == nums.length) {
            // 如果当前路径和等于目标值，则方案数量加 1
            if (path == aim) ret++;
            return; // 结束当前递归
        }

        // 尝试将当前数字作为加法项
        dfs(nums, pos + 1, path + nums[pos]); // 将当前数字加到路径和中，递归到下一个数字
        // 尝试将当前数字作为减法项
        dfs(nums, pos + 1, path - nums[pos]); // 将当前数字减到路径和中，递归到下一个数字
    }
}

1.7 组合总和

题目链接：组合总和

class Solution {
    int aim; // 目标值 target
    List<Integer> path; // 用于存储当前路径（一个组合）
    List<List<Integer>> ret; // 用于存储所有满足条件的组合

    public List<List<Integer>> combinationSum(int[] nums, int target) {
        path = new ArrayList<>(); 
        ret = new ArrayList<>(); 
        aim = target; 

        dfs(nums, 0, 0); // 从第一个数字开始深度优先搜索，初始路径和为 0
        return ret; 
    }

    public void dfs(int[] nums, int pos, int sum) {
        // 如果当前路径和等于目标值，说明找到一个合法组合
        if (sum == aim) {
            ret.add(new ArrayList<>(path)); 
            return;
        }

        // 如果路径和超过目标值，或者遍历到数组末尾，直接返回
        if (sum > aim || pos == nums.length) return;

        // 枚举当前数字 nums[pos] 可以使用多少次（从 0 开始）
        for (int k = 0; k * nums[pos] + sum <= aim; k++) {
            if (k != 0) path.add(nums[pos]); // 如果使用了当前数字，加入路径
            dfs(nums, pos + 1, sum + k * nums[pos]); // 递归处理下一个数字
        }

        // 恢复现场：移除在路径中加入的当前数字
        for (int k = 1; k * nums[pos] + sum <= aim; k++) {
            path.remove(path.size() - 1); // 从路径末尾依次移除当前数字
        }
    }
}

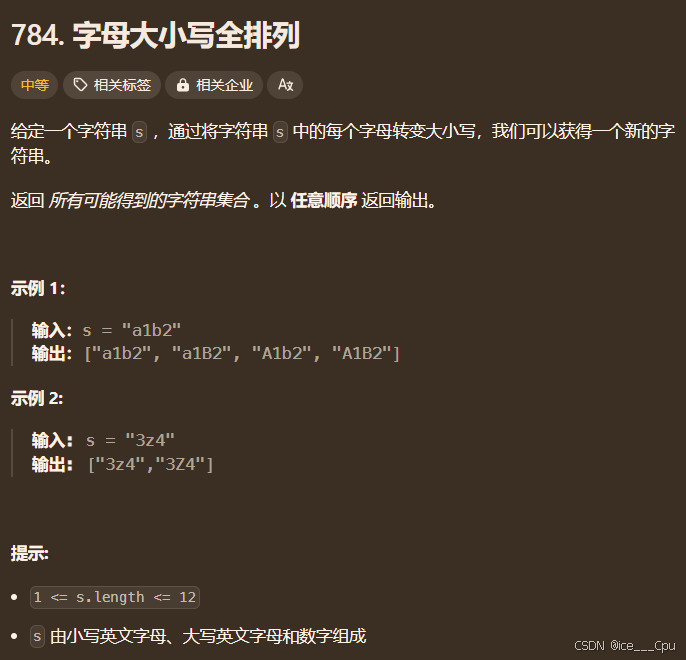
1.8 字母大小写全排列

题目链接：字母大小写全排列

class Solution {
    StringBuffer path; // 用于存储当前路径（字符串的一个变种）
    List<String> ret;  // 用于存储所有符合条件的字符串变种

    public List<String> letterCasePermutation(String s) {
        path = new StringBuffer(); 
        ret = new ArrayList<>();  
        dfs(s, 0); 
        return ret; 
    }

    public void dfs(String s, int pos) {
        // 递归出口：如果当前路径已经包含完整的字符串长度
        if (pos == s.length()) {
            ret.add(path.toString()); // 将当前路径的字符串形式加入结果集
            return; 
        }

        char ch = s.charAt(pos); 

        // 第一种选择：不改变当前字符的大小写
        path.append(ch);          
        dfs(s, pos + 1);          
        path.deleteCharAt(path.length() - 1); 

        // 第二种选择：改变当前字符的大小写（如果是字母）
        if (ch < '0' || ch > '9') { 
            char tmp = change(ch);  
            path.append(tmp);       
            dfs(s, pos + 1);        
            path.deleteCharAt(path.length() - 1); 
        }
    }

    public char change(char ch) {
        // 如果是小写字母，将其转换为大写字母
        if (ch >= 'a' && ch <= 'z') return (char) (ch - 32);
        // 如果是大写字母，将其转换为小写字母
        else return (char) (ch + 32);
    }
}

1.9 优美的排列

题目链接：优美的排列

class Solution {
    boolean[] check; // 用于记录某个数字是否已经被使用
    int ret;         // 用于记录符合条件的排列数量

    public int countArrangement(int n) {
        // 初始化 `check` 数组，大小为 n + 1（从 1 开始计数）
        check = new boolean[n + 1];
        ret = 0; 
        dfs(1, n); // 从位置 1 开始进行深度优先搜索
        return ret; 
    }

    public void dfs(int pos, int n) {
        // 递归出口：当位置 `pos` 超过 `n`，说明找到一个合法排列
        if (pos == n + 1) {
            ret++; // 合法排列计数加 1
            return; 
        }

        // 遍历从 1 到 n 的每个数字，尝试将其放在当前位置 `pos`
        for (int i = 1; i <= n; i++) {
            // 检查当前数字是否符合条件：
            // 1. 数字 `i` 未被使用（`check[i] == false`）。
            // 2. 满足 `i % pos == 0` 或 `pos % i == 0`。
            if (!check[i] && (i % pos == 0 || pos % i == 0)) {
                check[i] = true; 
                dfs(pos + 1, n); 
                check[i] = false; 
            }
        }
    }
}

1.10 N 皇后

题目链接：N 皇后

class Solution {
    boolean[] checkCol, checkDig1, checkDig2;  // 定义三个布尔数组，用于判断某列、主对角线、副对角线是否已经放置过皇后
    List<List<String>> ret;   // 存储最终结果的列表，每个结果是一个 N 皇后的解
    char[][] path;  // 当前路径，用一个二维字符数组表示棋盘
    int n;   // 棋盘的大小

    public List<List<String>> solveNQueens(int _n) {
        n = _n; 

        // 初始化布尔数组，分别表示某列、主对角线、副对角线是否被占用
        checkCol = new boolean[n];
        checkDig1 = new boolean[n * 2]; // 主对角线的数量是 2n - 1，这里用 2n 防止数组越界
        checkDig2 = new boolean[n * 2]; // 副对角线的数量同上
        ret = new ArrayList<>(); 
        path = new char[n][n]; // 初始化棋盘，每个位置用 '.' 表示空位
        for (int i = 0; i < n; i++) {
            Arrays.fill(path[i], '.');
        }

        dfs(0); // 从第 0 行开始深度优先搜索
        return ret; // 返回所有结果
    }

    public void dfs(int row) {
        // 递归出口：当 row == n 时，表示所有行都已成功放置皇后
        if (row == n) {
            // 将当前路径转换为一个结果并添加到 ret 中
            List<String> tmp = new ArrayList<>();
            for (int i = 0; i < n; i++) {
                tmp.add(new String(path[i]));
            }
            ret.add(new ArrayList<>(tmp)); 
            return;
        }

        // 遍历当前行的每一列，尝试放置皇后
        for (int col = 0; col < n; col++) {
            // 判断当前位置 (row, col) 是否可以放置皇后
            if (checkCol[col] == false && 
                checkDig1[row - col + n] == false && 
                checkDig2[row + col] == false) {
                // 如果可以放置，更新棋盘和标记数组
                path[row][col] = 'Q'; // 在当前位置放置皇后
                checkCol[col] = true; // 标记当前列为已占用
                checkDig1[row - col + n] = true; // 标记主对角线为已占用
                checkDig2[row + col] = true; // 标记副对角线为已占用

                dfs(row + 1); // 递归到下一行

                // 恢复现场，回溯
                path[row][col] = '.'; 
                checkCol[col] = false; 
                checkDig1[row - col + n] = false; 
                checkDig2[row + col] = false; 
            }
        }
    }
}

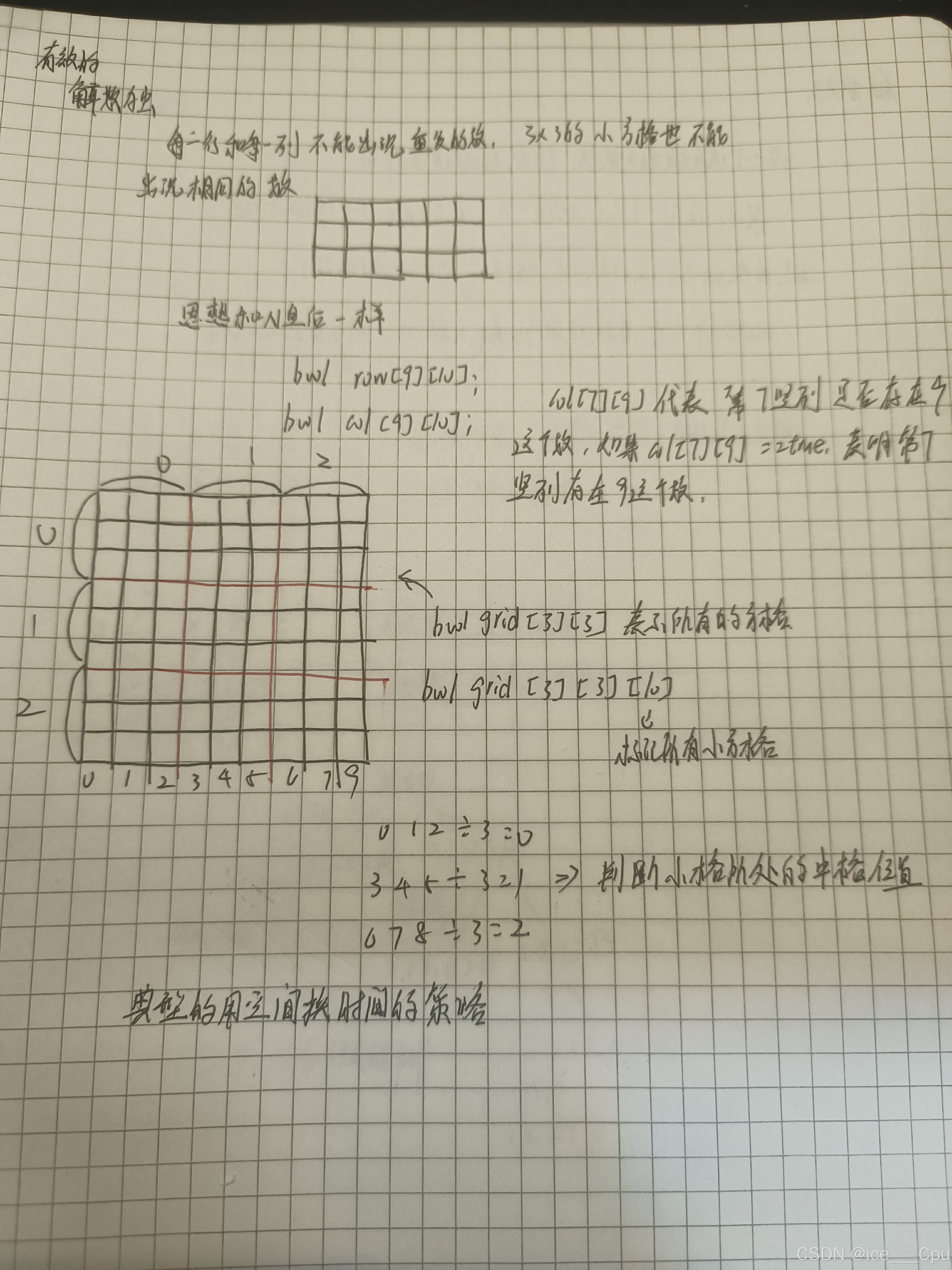
1.11 有效的数独

题目链接：有效的数独

class Solution {
    // 用于记录每行是否存在某个数字，row[7][9] 代表第 7 行中有 9 这个数字
    boolean[][] row;
    // 用于记录每列是否存在某个数字，col[7][0] 代表第 7 列中有 9 这个数字
    boolean[][] col;
    // 用于记录每个3x3子网格是否存在某个数字，grid[2][1][8] 代表第第三行第二列的 3x3 的子网格有数字 8
    boolean[][][] grid;

    public boolean isValidSudoku(char[][] board) {
        // 初始化行、列、和子网格的检查数组
        // 数字范围是 1-9，而数组索引是从 0 开始的，所以我们浪费一个空间，简化代码逻辑，避免计算额外的偏移量。
        row = new boolean[9][10]; // 9行，数字范围1-9
        col = new boolean[9][10]; // 9列，数字范围1-9
        grid = new boolean[3][3][10]; // 3x3子网格，数字范围1-9

        // 遍历整个棋盘
        for (int i = 0; i < 9; i++) { 
            for (int j = 0; j < 9; j++) { 
                if (board[i][j] != '.') { 
                    int num = board[i][j] - '0'; // 将字符转换为数字 '5' -> 5

                    // 检查当前数字是否在对应行、列或子网格中已经存在，如果存在冲突，则数独无效
                    if (row[i][num] || col[j][num] || grid[i / 3][j / 3][num]) return false; 
                    
                    // 如果没有冲突，将该数字标记为已存在
                    row[i][num] = true; // 标记该数字在当前行出现过
                    col[j][num] = true; // 标记该数字在当前列出现过
                    grid[i / 3][j / 3][num] = true; // 标记该数字在所属的3x3子网格中出现过
                }
            }
        }

        // 如果遍历完成后没有冲突，说明数独有效
        return true;
    }
}

1.12 解数独

题目链接：解数独

class Solution {
    // 解题思路和 有效的数独 类似，可以参考上题的代码

    boolean[][] row, col; // 用于记录每行是否存在某个数字
    boolean[][][] grid; // 用于记录每个 3x3 子网格是否存在某个数字

    public void solveSudoku(char[][] board) {
        // 初始化行、列、子网格的状态数组
        row = new boolean[9][10]; 
        col = new boolean[9][10]; 
        grid = new boolean[3][3][10]; 

        // 遍历整个数独棋盘，初始化状态
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                if (board[i][j] != '.') { // 这题中 . 代表空格
                    int num = board[i][j] - '0'; 
                    // 更新对应行、列和子网格的状态为已占用
                    row[i][num] = true;
                    col[j][num] = true;
                    grid[i / 3][j / 3][num] = true;
                }
            }
        }

        // 开始递归求解
        dfs(board);
    }

    public boolean dfs(char[][] board) {
        // 遍历棋盘寻找空白位置
        for (int i = 0; i < 9; i++) {
            for (int j = 0; j < 9; j++) {
                if (board[i][j] == '.') { 
                    // 尝试填入数字 1-9
                    for (int num = 1; num <= 9; num++) {
                        // 剪枝：如果当前数字在行、列或子网格中已存在，则跳过
                        if (!row[i][num] && !col[j][num] && !grid[i / 3][j / 3][num]) {
                            // 填入当前数字，并更新状态
                            board[i][j] = (char) ('0' + num); // 将数字转回字符填入棋盘
                            row[i][num] = true;
                            col[j][num] = true;
                            grid[i / 3][j / 3][num] = true;

                            // 递归尝试填下一个空格
                            if (dfs(board)) return true; // 如果成功返回 true，解已找到

                            // 回溯：恢复现场，将之前的修改还原
                            board[i][j] = '.';
                            row[i][num] = false;
                            col[j][num] = false;
                            grid[i / 3][j / 3][num] = false;
                        }
                    }
                    // 如果 1-9 都无法填入当前空格，说明无解，返回 false
                    return false;
                }
            }
        }
        // 如果遍历完整个棋盘没有遇到空格，说明已成功解出数独
        return true;
    }
}

1.13 单词搜索

题目链接：单词搜索

class Solution {
    boolean[][] vis; // 访问标记数组，记录某个位置是否被访问过
    int m, n; // 棋盘的行数和列数
    char[] word; // 目标单词的字符数组形式

    public boolean exist(char[][] board, String _word) {
        // 初始化行数和列数以及 vis 数组，并把目标字符串转为字符数组，方便操作，vis 默认全为 false
        m = board.length;
        n = board[0].length;
        vis = new boolean[m][n];
        word = _word.toCharArray();

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                // 如果当前格子的字符和目标单词的第一个字符相等
                if (board[i][j] == word[0]) {
                    // 标记当前位置为已访问
                    vis[i][j] = true;
                    // 从当前位置开始尝试匹配单词的后续字符
                    if (dfs(board, i, j, 1) == true) return true;
                    // 回溯：恢复访问标记
                    vis[i][j] = false;
                }
            }
        }
        // 如果遍历所有起点后仍无法匹配完整单词，返回 false
        return false;
    }

    // 用于表示上下左右四个方向的移动向量
    int[] dx = {0, 0, 1, -1};
    int[] dy = {1, -1, 0, 0};

    /**
     * 深度优先搜索
     * @param board 当前棋盘
     * @param i 当前格子的行坐标
     * @param j 当前格子的列坐标
     * @param pos 当前需要匹配的单词字符的索引
     * @return 是否能成功匹配到完整单词
     */
    public boolean dfs(char[][] board, int i, int j, int pos) {
        // 如果 pos 等于单词长度，说明单词已成功匹配
        if (pos == word.length) return true;
        
        // 遍历当前格子上下左右四个方向
        for (int k = 0; k < 4; k++) {
            // 计算新格子的坐标
            int x = i + dx[k], y = j + dy[k];
            // 判断新格子是否在边界内，未被访问过，且字符匹配
            if (x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && board[x][y] == word[pos]) {
                // 标记新格子为已访问
                vis[x][y] = true;
                // 递归继续匹配下一个字符
                if (dfs(board, x, y, pos + 1) == true) return true;
                // 回溯：恢复访问标记
                vis[x][y] = false;
            }
        }
        // 如果四个方向都无法匹配，返回 false
        return false;
    }
}

1.14 黄金矿工 I

题目链接：黄金矿工 I

class Solution {
    // 用于表示上下左右四个方向的移动向量
    int[] dx = {0, 0, -1, 1};
    int[] dy = {1, -1, 0, 0};
    boolean[][] vis; // 访问标记数组，记录某个位置是否已经访问过
    int m, n; // 网格的行数和列数
    int ret; // 保存当前能够获取的最大黄金量

    public int getMaximumGold(int[][] g) {
        // 初始化行数和列数以及 vis 数组
        m = g.length;
        n = g[0].length;
        vis = new boolean[m][n];

        // 接着遍历每个网格单元
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                // 如果当前单元格的黄金量不为 0，则尝试以此为起点开始探索
                if (g[i][j] != 0) {
                    vis[i][j] = true;
                    dfs(g, i, j, g[i][j]); // 进行深度优先搜索，从当前单元开始累积黄金量
                    vis[i][j] = false; // 回溯：恢复访问状态
                }
            }
        }
        // 返回能获取的最大黄金量
        return ret;
    }

    /**
     * 深度优先搜索
     * @param g 网格
     * @param i 当前格子的行坐标
     * @param j 当前格子的列坐标
     * @param path 当前路径累积的黄金量
     */
    public void dfs(int[][] g, int i, int j, int path) {
        // 首先更新最大黄金量
        ret = Math.max(ret, path);

        // 遍历上下左右四个方向
        for (int k = 0; k < 4; k++) {
            int x = i + dx[k], y = j + dy[k]; // 计算新的位置
            // 判断新位置是否合法：在边界内、未被访问过、黄金量不为 0
            if (x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && g[x][y] != 0) {
                vis[x][y] = true;
                dfs(g, x, y, path + g[x][y]); // 递归继续搜索，将当前格子的黄金量累加到路径中
                vis[x][y] = false; // 回溯：恢复访问状态
            }
        }
    }
}

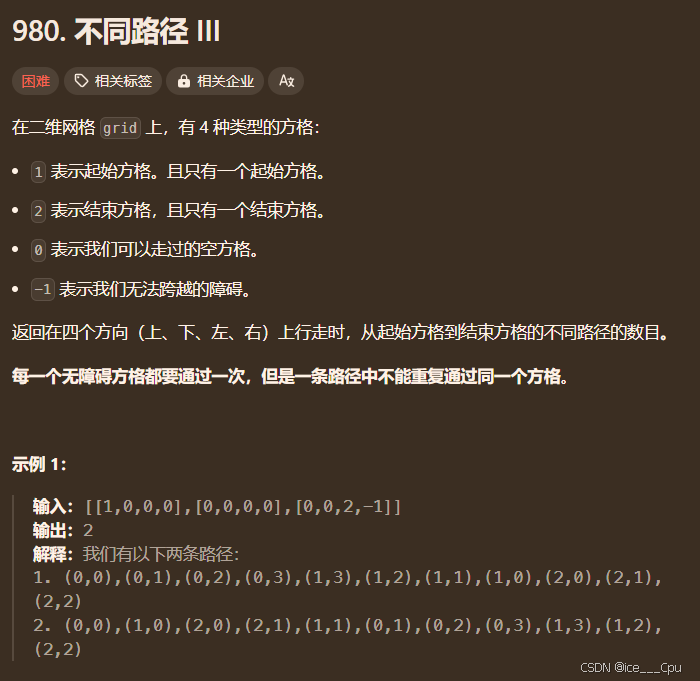
1.15 不同路径 III

题目链接：不同路径 III

class Solution {
    // 用于表示上下左右四个方向的移动向量
    int[] dx = {0, 0, 1, -1};
    int[] dy = {1, -1, 0, 0};
    boolean[][] vis; // 访问标记数组，记录某个位置是否被访问过
    int m, n; // 网格的行数和列数
    int step; // 记录需要走的总步数，包括起点和终点
    int ret; // 记录结果，即有效路径的数量
    
    public int uniquePathsIII(int[][] grid) {
        // 初始化网格的行数和列数
        m = grid.length;
        n = grid[0].length;
        vis = new boolean[m][n];
        int bx = 0, by = 0; // 起点坐标

        // 遍历整个网格，确定起点、终点和需要经过的格子数量
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (grid[i][j] == 0) step++;
                else if (grid[i][j] == 1) {
                    bx = i; by = j;
                }
            }
        }

        step += 2; // 总步数：包括起点和终点，所以需要加 2
        vis[bx][by] = true; // 标记起点为已访问

        dfs(grid, bx, by, 1); // 从起点开始深度优先搜索

        return ret; // 返回所有符合条件的路径数量
    }

    /**
     * 深度优先搜索
     * @param grid 当前网格
     * @param i 当前格子的行坐标
     * @param j 当前格子的列坐标
     * @param count 当前已走的步数
     */
    public void dfs(int[][] grid, int i, int j, int count) {
        // 如果到达终点
        if (grid[i][j] == 2) {
            // 判断是否经过了所有需要经过的格子
            if (count == step) ret++; // 如果满足条件，路径计数加 1
            else return;
        }

        // 遍历上下左右四个方向
        for (int k = 0; k < 4; k++) {
            int x = i + dx[k], y = j + dy[k];
            // 判断新位置是否合法：在边界内、未被访问过、不是障碍物
            if (x >= 0 && x < m && y >= 0 && y < n && !vis[x][y] && grid[x][y] != -1) {
                vis[x][y] = true;
                dfs(grid, x, y, count + 1); // 递归探索下一步，同时步数加 1
                vis[x][y] = false; // 回溯：恢复访问状态
            }
        }
    }
}