Bootstrap

二叉树的线索化

1.为什么要对二叉树进行线索化？
一棵普通的二叉树，只能找到该节点的左右孩子信息，并不能知道该节点的直接前驱或后继信息。这种信息只有在动态遍历的过程中才能得到，因此我们引入线索二叉树来保存这些动态过程中得到的前驱和后继的信息。有n个节点的二叉树，必定存在n+1个空指针域，我们可以充分利用这些空指针域，来保存当前节点的前驱和后继信息。
在这里，我们引入了两个标志位，LINK和THREAD，如果当前节点的左孩子为NULL,就让当前节点指向该节点的前驱，否则继续向下遍历，知道左孩子为空结束，此时需要将该节点对应的标志位改为THREAD；接下来遍历该节点的右孩子，如果当前节点的右孩子为空，就让该节点指向该节点的后继，并将该节点的标志位设置为THREAD
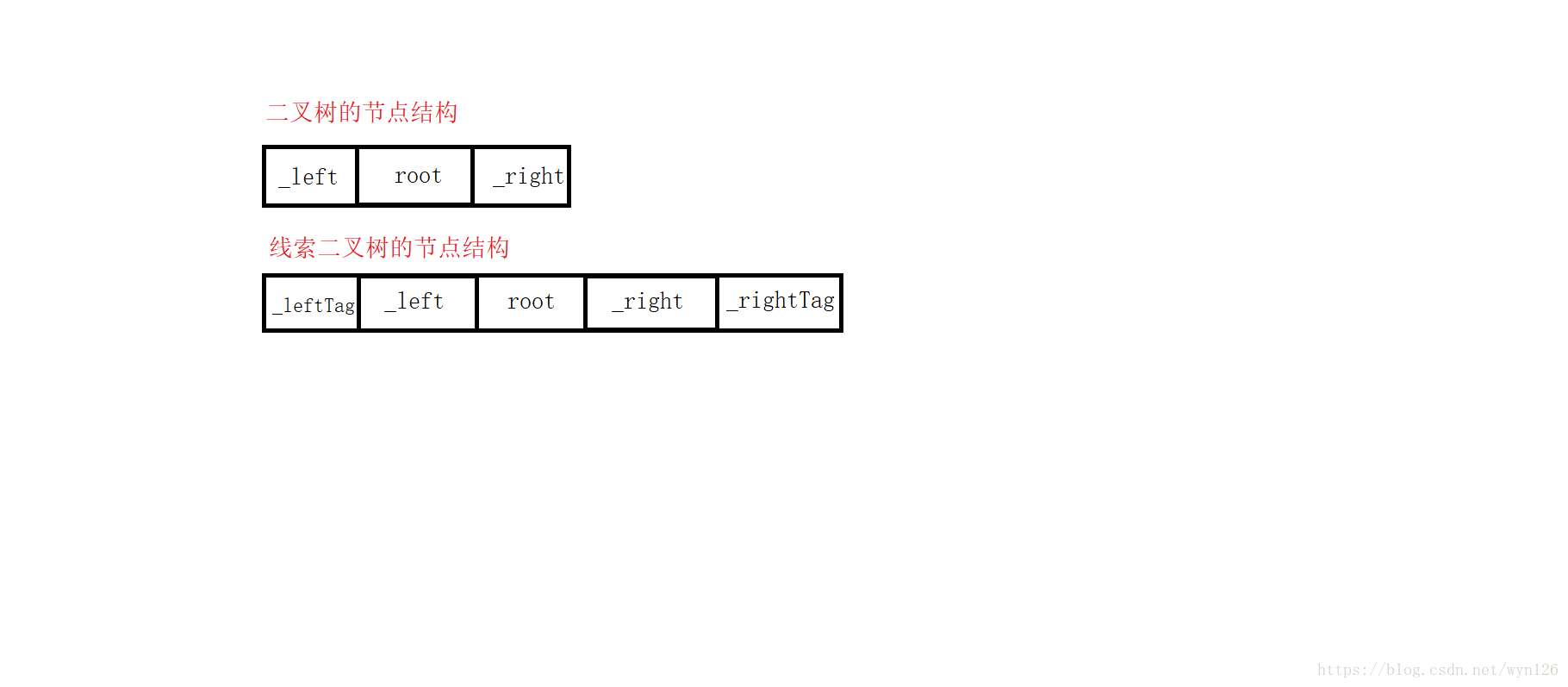
下来我们来研究一下节点的结构信息

enum PointerTag
{
    THREAD,     //表示该节点需要被线索化
    LINK          //表示该节点不需要进行线索化，继续向下遍历
};
template<class T>
struct BinaryTreeNodeThd
{
    T _data;
    BinaryTreeNodeThd<T>*  _left;
    BinaryTreeNodeThd<T>*  _right;
    PointerTag _leftTag;
    PointerTag _rightTag;
    BinaryTreeNodeThd(const T& x)
        :_data(x)
        , _left(NULL)
        , _right(NULL)
        , _leftTag(LINK)  //在定义一个树的节点时，树的左右孩子都没有被初始化，所以标记为都是LINK
        , _rightTag(LINK)
    {}
};

相对于二叉树的节点结构来说，线索二叉树的节点结构里增加了标志位
这里写图片描述
线索化的概念：对二叉树以某种顺序进行遍历使其变成线索二叉树的过程叫做线索化。
2.构造线索化二叉树
线索二叉树构造的实质是在遍历的时候将二叉链表中的空指针指向改为指向该节点的前驱或者后继，而前驱和后继的信息只有在遍历的时候才能够得到，为了记录遍历过程中访问节点的先后顺序，我们可以设置一个Prev指针来记录上一个刚刚访问过的节点，root表示正在访问的节点。以中序为例来分析一下线索化的过程：
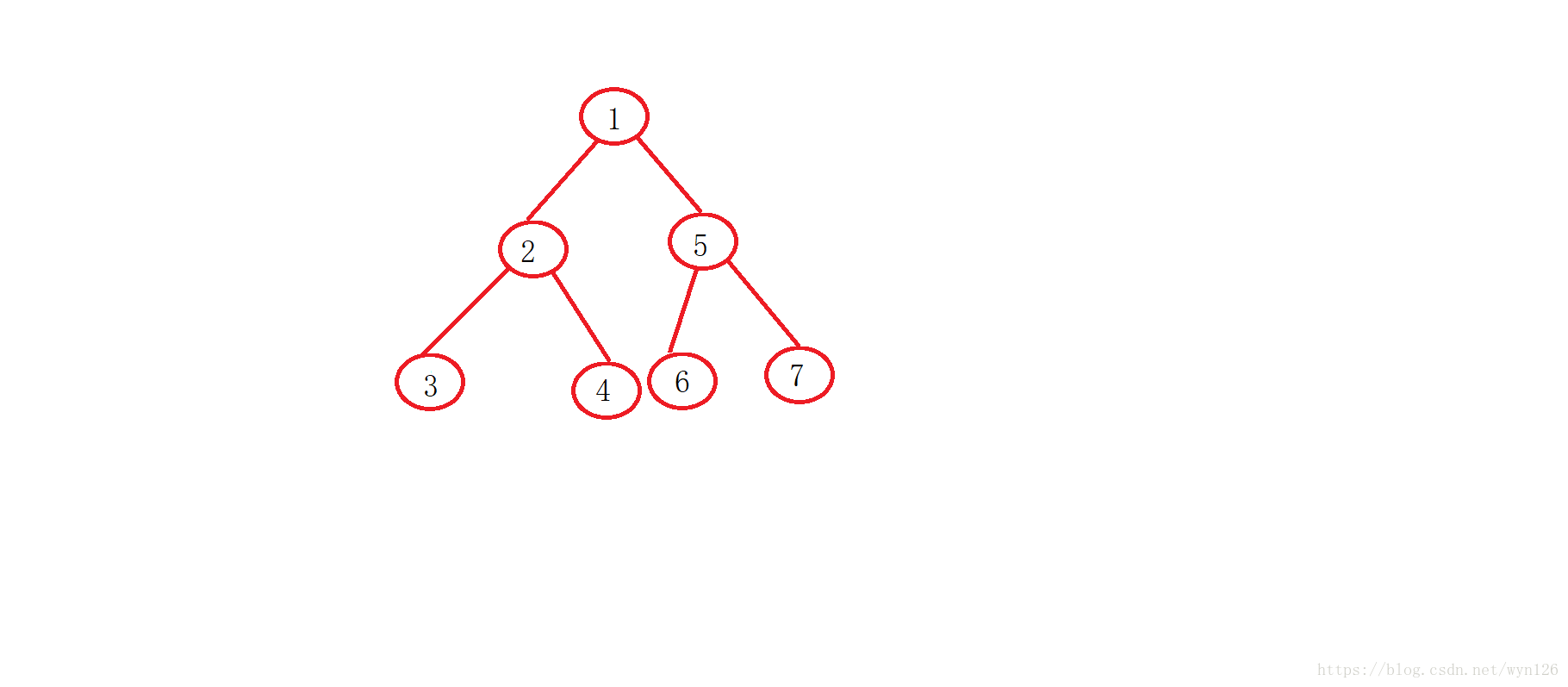
这里写图片描述
中序的访问顺序是：先访问左子树，再访问根节点，最后访问右子树
//中序线索化
（1）用Prev表示上一个刚刚出现过的节点，这样就很容易找到该节点的前驱
（2）如何知道下一个出现的节点？
在中序遍历中，永远不知道下一个中序出现节点是谁，但是如果到达下一 个节点，一定知道上一个出现的节点是谁，如果上一个节点的右是空，说明上一个节点的右需要线索化，让上一个节点的右指向当前节点 比如说，当到达节点2时，节点2的上一个节点时节点3，节点3的右孩子为空，就让节点3的右孩子指向节点2
下来看看用代码如何实现

中序线索化

void _InOrderThd(Node* root,Node* &Prev)//出现左树为空或者右树为空，就需要线索化
    {
        if (root == NULL)
            return;
        _InOrderThd(root->_left,Prev);
        //root在这出现的顺序就是中序  上一层结构设置的栈帧，用引用
        if (root->_left == NULL)
        {
            root->_left = Prev;
            root->_leftTag = THREAD;
        }
        if (Prev&&Prev->_right==NULL)
        {
            Prev->_right = root;
            Prev->_rightTag = THREAD;
        }
        Prev = root;
        _InOrderThd(root->_right,Prev);
    }

前序线索化

void _PrevOrderThd( Node* root, Node* &Prev)//前序线索化
    {
        if (root == NULL)
            return;
        if (root->_left == NULL)
        {
            root->_left = Prev;
            root->_leftTag = THREAD;
        }
        if (Prev&&Prev->_right == NULL)//只有是LINK时才需要继续走
        {
            Prev->_right = root;
            root->_rightTag = THREAD;
        }
        Prev = root;
        if (root->_leftTag == LINK)//避免死循环
        {
            _PrevOrderThd(root->_left, Prev);
        }
        if (root->_rightTag == LINK)
        {
            _PrevOrderThd(root->_right, Prev);
        }
    }

3.遍历线索二叉树
由于对二叉树进行了线索化，就有了节点前驱和后继的信息，这样就很容易查找当前节点的前驱和后继信息。
以中序为例：
查找当前节点的前驱
（1）如果当前节点的_leftTag为THREAD,那么当前节点指向该节点的前驱
（2）如果当前节点的_leftTag为LINK,，说明该节点有左子树，那么该节点的 前驱指向该节点左孩子的最右子树
查找当前节点的后继
（1）如果当前节点的_rightTag为THREAD,那么当前节点指向该节点的后继
（2）如果当前节点的_rightTag为LINK,说明该节点有右孩子，该节点的后继指向右孩子的最左节点
下来用代码实现二叉树的中序遍历

//中序遍历线索化，参考非递归，不需要定义栈
    //中序遍历，遇到一棵树，先找这棵树的最左节点，最先不被访问节点一定是最左节点，
    //当前节点访问完成需要再访问其右树
    //1、如果当前节点的右为LINK,当作子问题
    //2.如果当前节点的左为THREAD,直接跳转
    //最后访问的节点右树一定是空
    void InOrderThread()//用线索化进行遍历
    {
        Node* cur = _root;
        while (cur)
        {
            //先找第一个需要被访问的节点->最左节点
            while (cur->_leftTag == LINK)
            {
                cur = cur->_left;
            }
            cout << cur->_data << " ";
            /*到这里，cur的右树还没有被访问
            1、右为子树
            2、右为THREDAD，一定会跳到当前节点的父亲
            第一种写法*/
            //while (cur->_rightTag==THREAD)
            //{
            //  //跳到后继节点直接访问
            //  cur = cur->_right;
            //  cout<<cur->_data<<" ";
   //         }
            子问题c，ur的右树为LINK,子树
            //cur = cur->_right;
            if (cur->_rightTag == LINK)
            {
                cur = cur->_right;
            }
            else
            {
                while (cur->_rightTag == THREAD)
                {
                    cur = cur->_right;
                    cout << cur->_data<<" ";
                }
                cur = cur->_right;
            }
        }
        cout << endl;
    }

二叉树前序、中序、后序线索化和遍历的全部代码

#pragma once
enum PointerTag
{
    THREAD,
    LINK
};
template<class T>
struct BinaryTreeNodeThd
{
    T _data;
    BinaryTreeNodeThd<T>*  _left;
    BinaryTreeNodeThd<T>*  _right;
    PointerTag _leftTag;
    PointerTag _rightTag;
    BinaryTreeNodeThd(const T& x)
        :_data(x)
        , _left(NULL)
        , _right(NULL)
        , _leftTag(LINK)
        , _rightTag(LINK)
    {}
};
template <class T>
class BinaryTreeThd
{
    typedef BinaryTreeNodeThd<T> Node;
public:

    BinaryTreeThd(T* a, size_t n,const T& invalid)
    {
        size_t index = 0;
        _root = _CreateTree(a, n, invalid, index);
    }
    void PrevOrder()//前序遍历
    {
        _PrevOrder(_root);
        cout << endl;
    }
    void PrevOrderThd()//前序线索化
   {
        Node* Prev = NULL;
        _PrevOrderThd(_root, Prev);
    }
    void InOrderThd()//中序线索化
    {
        Node* Prev =NULL;
        _InOrderThd(_root, Prev);
    }
    //中序遍历线索化，参考非递归，不需要定义栈
    //中序遍历，遇到一棵树，先找这棵树的最左节点，最先不被访问节点一定是最左节点，
    //当前节点访问完成需要再访问其右树
    //1、如果当前节点的右为LINK,当作子问题
    //2.如果当前节点的左为THREAD,直接跳转
    //最后访问的节点右树一定是空
    void InOrderThread()//用线索化进行遍历
    {
        Node* cur = _root;
        while (cur)
        {
            //先找第一个需要被访问的节点->最左节点
            while (cur->_leftTag == LINK)
            {
                cur = cur->_left;
            }
            cout << cur->_data << " ";
            /*到这里，cur的右树还没有被访问
            1、右为子树
            2、右为THREDAD，一定会跳到当前节点的父亲
            第一种写法*/
            //while (cur->_rightTag==THREAD)
            //{
            //  //跳到后继节点直接访问
            //  cur = cur->_right;
            //  cout<<cur->_data<<" ";
   //         }
            子问题c，ur的右树为LINK,子树
            //cur = cur->_right;
            if (cur->_rightTag == LINK)
            {
                cur = cur->_right;
            }
            else
            {
                while (cur->_rightTag == THREAD)
                {
                    cur = cur->_right;
                    cout << cur->_data<<" ";
                }
                cur = cur->_right;
            }
        }
        cout << endl;
    }

protected:
    Node* _CreateTree(T* a, size_t n, const T& invalid, size_t &index)//index用引用，递归里面++要给上一层使用
    {
        Node* root = NULL;
        if (index < n && a[index] != invalid)
        {
            root = new Node(a[index]);
            root->_left = _CreateTree(a, n, invalid, ++index);
            root->_right = _CreateTree(a, n, invalid, ++index);
        } 
        return  root;
    }
    //void _PrevOrder(Node* root)//前序遍历,注意线索化之后不能像之前那样遍历
    //{
    //  if (root == NULL)
    //      return;
    //  cout << root->_data<<" ";//访问根节点
    //  _PrevOrder(root->_left);//访问左子树
    //  _PrevOrder(root->_right);//访问右子树
    //}
    void _PrevOrder(Node* root)//前序遍历,注意线索化之后不能像之前那样遍历
    {
        if (root == NULL)
            return;
        cout << root->_data << " ";//访问根节点
        if (root->_leftTag == LINK)//避免死循环
        {
            _PrevOrder(root->_left);//访问左子树
        }
        if (root->_rightTag == LINK)
        {
            _PrevOrder(root->_right);//访问右子树
        }
    }
    void _PrevOrderThd( Node* root, Node* &Prev)//前序线索化
    {
        if (root == NULL)
            return;
        if (root->_left == NULL)
        {
            root->_left = Prev;
            root->_leftTag = THREAD;
        }
        if (Prev&&Prev->_right == NULL)//只有是LINK时才需要继续走
        {
            Prev->_right = root;
            root->_rightTag = THREAD;
        }
        Prev = root;
        if (root->_leftTag == LINK)//避免死循环
        {
            _PrevOrderThd(root->_left, Prev);
        }
        if (root->_rightTag == LINK)
        {
            _PrevOrderThd(root->_right, Prev);
        }
    }
    //中序线索化
    //1、用Prev表示上一个出现过的节点
    //2、如何知道下一个出现的节点，在中序遍历中，永远不知道下一个中序出现节点是谁，
    //但是如果到达下一个节点，一定知道上一个出现的节点是谁，如果上一个节点的右是空，说明
    //上一个节点的右需要线索化，让上一个节点的右指向当前节点
    void _InOrderThd(Node* root,Node* &Prev)//出现左树为空或者右树为空，就需要线索化
    {
        if (root == NULL)
            return;
        _InOrderThd(root->_left,Prev);
        //root在这出现的顺序就是中序  上一层结构设置的栈帧，用引用
        if (root->_left == NULL)
        {
            root->_left = Prev;
            root->_leftTag = THREAD;
        }
        if (Prev&&Prev->_right==NULL)
        {
            Prev->_right = root;
            Prev->_rightTag = THREAD;
        }
        Prev = root;
        _InOrderThd(root->_right,Prev);
    }

protected:
    Node *_root;
};
//一棵树只能被线索化成为一种顺序
int main()
{
    int arr[10] = { 1, 2, 3, '#', '#', 4, '#', '#', 5, 6 };
    BinaryTreeThd<int> t1(arr, sizeof(arr) / sizeof(arr[0]), '#');
    t1.PrevOrder();
    t1.InOrderThd();
    t1.InOrderThread();

}

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
染色问题（并查集）
如何在HTML中使用React
UML类与类的关系, 总算理解了关联和依赖在实际中的区别
Beans模块之工厂模块ObjectProvider
Python 新一代 HTTP 请求库：httpx
JUC高并发编程学习1
Android10系统ROM定制之Frida逆向分析实战
Vue项目中使用@代替src——并在VScode中开启@路径自动提示
html5 canvas获取坐标,HTML5 canvas坐标
SEU使用Linux命令行登录校园网方法
;