支持向量机(SVM)算法
支持向量机(SVM)是一种功能强大的机器学习算法,广泛用于线性和非线性分类以及回归和异常值检测任务。SVM 具有很强的适应性,适用于各种应用,例如文本分类、图像分类、垃圾邮件检测、笔迹识别、基因表达分析、人脸检测和异常检测。
SVM 特别有效,因为它们专注于寻找目标特征中不同类别之间的最大分离超平面,从而使其对二分类和多分类都具有鲁棒性。在本大纲中,我们将探讨支持向量机 (SVM)算法、其应用以及它如何有效地处理线性和非线性分类以及回归和异常值检测任务。
目录
- 支持向量机
- 支持向量机算法如何工作?
- 支持向量机术语
- 数学计算:SVM
- 支持向量机的类型
- SVM中的流行核函数
- 在 Python 中实现 SVM 算法
- 支持向量机(SVM)的优点和缺点
支持向量机
支持向量机(SVM)是一种监督式机器学习算法,可用于分类和回归任务。虽然 SVM 可以应用于回归问题,但它最适合用于分类任务。SVM算法的主要目标是在 N 维空间中确定最佳超平面,该超平面可以有效地将数据点分为特征空间中的不同类别。该算法可确保不同类别的最近点(称为支持向量)之间的边距最大化。
超平面的维度取决于特征的数量。例如,如果有两个输入特征,超平面就是一条线,如果有三个输入特征,超平面就变成一个二维平面。随着特征数量超过三个,可视化超平面的复杂性也会增加。
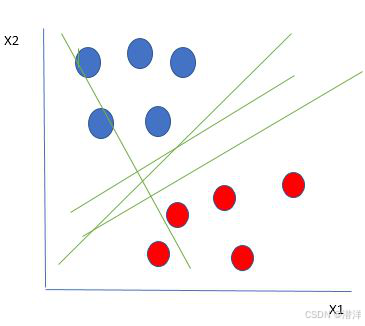
考虑两个独立变量x1和x2,以及一个因变量,用蓝色圆圈或红色圆圈表示。
- 在这种情况下,超平面是一条线,因为我们正在处理两个特征(x1和x2)。
- 有多条线(或超平面)可以分隔数据点。
- 挑战在于确定最大化红色和蓝色圆圈之间分离边缘的最佳超平面。
线性可分离数据点
从上图中可以清楚地看出,有多条线(此处的超平面是一条线,因为我们只考虑两个输入特征 x 1、 x 2)将我们的数据点分隔开或在红色和蓝色圆圈之间进行分类。那么我们如何选择最佳的线或一般来说最佳的超平面来分隔我们的数据点呢?
支持向量机算法如何工作?
支持向量机 (SVM)中最佳超平面的一个合