1. 题目来源

链接：1186. 删除一次得到子数组最大和

• 强相关题目：
  • 前置+重要知识点：[Edp] lc53. 最大子序和(dp+分治+算法优化+详细分析)

2. 题目解析

该问题的一个基础问题是 [Edp] lc53. 最大子序和(dp+分治+算法优化+详细分析)。即采用 dp 的方式，$O(n)$ 求取数组中的最大子数组和。

回顾：

• 状态定义：f[i] 为以 i 为右端点的最大子数组和。
• 状态转移：f[i]=max(f[i-1]+a[i], a[i])=max(f[i-1], 0)+a[i] 这是一个常用的转换写法，想法也比较明确。如果 f[i-1] 都已经小于 0 了，那也不需要前面的这些子数组了。

看看本题：

• 本题要求可以删除一个元素 i，然后保证剩下的子数组最大。
• 最终子数组有两种形式：
  • 只包含一段元素，即不进行删除的情况。
  • 有两段元素，将 i 位置删除的情况
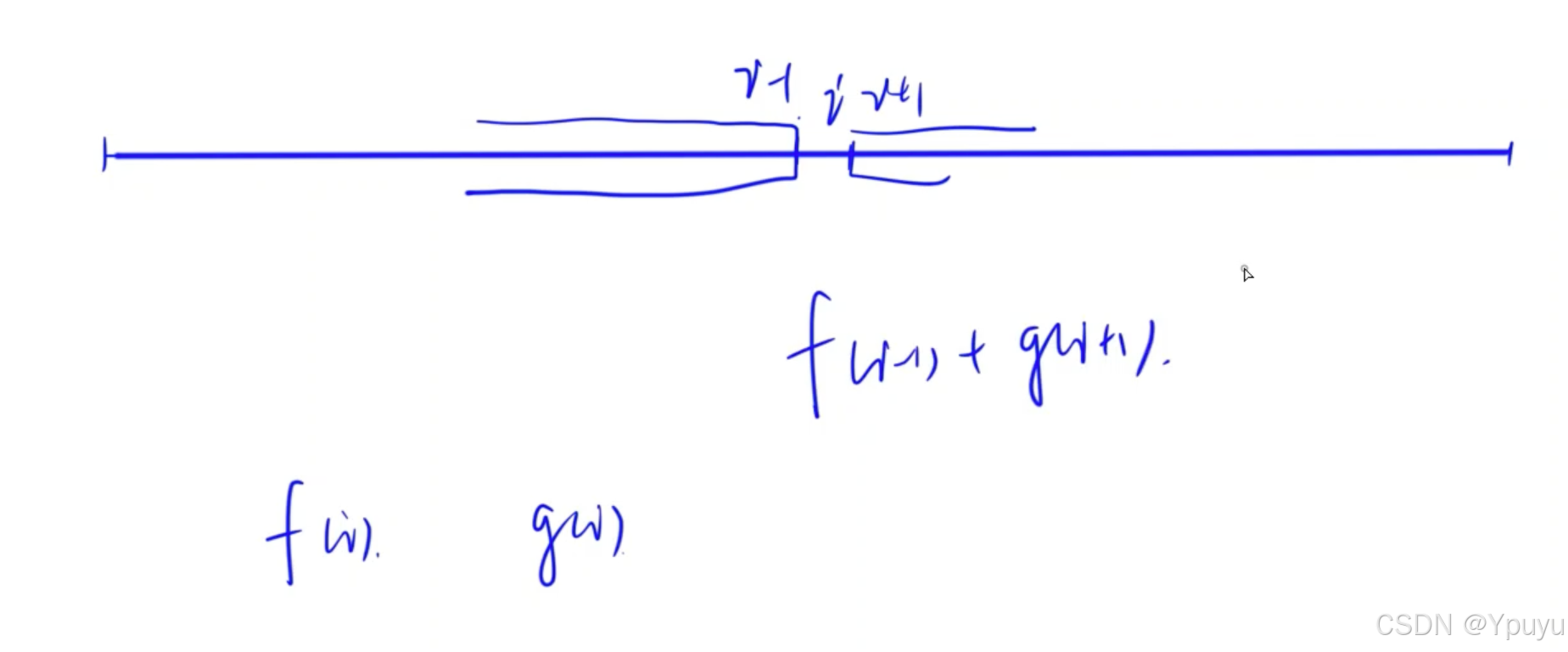
• 那么这个最终构成的子数组，可以转化为：以 i 为分界点，前缀是一个最大子段和、后缀是一个最大子段和。
• 我们已经得到了 f 是一个从 0~i 中，以 i 结尾的最大子段和子数组。
• 只需要再预处理得到一个 g，g 是一个从 i~n-1 中，以 i 结尾的最大子段和子数组。

如下图：

y 总还讲了一个状态机的思路，和官解感觉大差不差，但是转移方程不太一样。官解中讲解的是一个非常标准的一个 dp 思路，也可以看看。

其实重点还是 [Edp] lc53. 最大子序和(dp+分治+算法优化+详细分析) 这个问题，前后缀分解、改进dp 都是在这个基础之上产生的变种题目。

• 时间复杂度：$O(n)$
• 空间复杂度：$O(1)$

前后缀分解：

class Solution {
public:
    int maximumSum(vector<int>& arr) {
        int n = arr.size();
        vector<int> f(n), g(n);
        f[0] = arr[0], g[n - 1] = arr[n - 1];

        int res = f[0]; // 注意状态初始化，枚举最大值
        for (int i = 1; i < n; i ++ ) {
            f[i] = max(f[i - 1], 0) + arr[i];
            res = max(res, f[i]);  // 枚举第一种情况：不需要进行删除的一种情况，在 g 中枚举也是一样的
        }

        for (int j = n - 2; j >= 0; j -- ) {
            g[j] = max(g[j + 1], 0) + arr[j];
        }

        for (int i = 1; i < n - 1; i ++ ) {
            res = max(res, f[i - 1] + g[i + 1]);    // 枚举第二种情况：需要删除的场景，以 i 为分界点
        }

        return res;
    }
};