量子萤火虫算法(Quantum-behaved Firfly Algorithm,QFA)是对萤火虫算法的一种改进,旨在提升萤火虫个体的搜索能力。以下是对量子萤火虫算法的详细介绍:
一、萤火虫算法基础
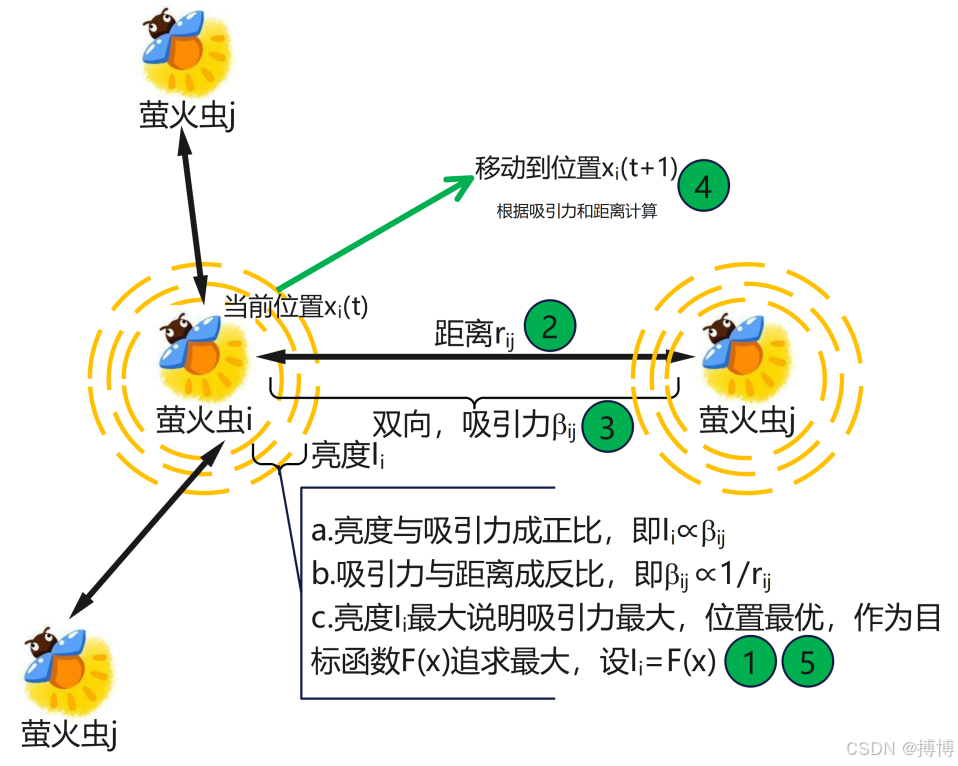
萤火虫算法(Firefly Algorithm,FA)是一种基于群体智能的优化算法,由剑桥大学的Xin-She Yang在2008年(也有说法为2009年)提出。该算法模拟萤火虫之间通过发光和相互吸引来实现搜索和优化的过程。在萤火虫算法中,每只萤火虫的亮度代表其优化目标函数值,亮度越高的萤火虫代表更优的解决方案。萤火虫会被周围更亮的萤火虫所吸引,并朝着更亮的萤火虫移动,从而实现搜索空间中的移动过程。
图1 经典萤火虫算法(FA)演示图
二、算法的特点
量子萤火虫算法结合了量子计算和萤火虫算法的优势,具有以下特点:
(1)量子编码与解码:在量子萤火虫算法中,量子个体(即萤火虫)的每个量子位的状态用概率幅度表示,通常用量子角形式(如![[\alpha, \beta ]^{T}=[cos\theta , sin\theta ]^{T}](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUIlNUNhbHBoYSUyQyUyMCU1Q2JldGElMjAlNUQlNUUlN0JUJTdEJTNEJTVCY29zJTVDdGhldGElMjAlMkMlMjBzaW4lNUN0aGV0YSUyMCU1RCU1RSU3QlQlN0Q%3D)
(2)量子搜索特性:量子萤火虫算法利用量子计算的并行性和不确定性,使得萤火虫在搜索过程中能够同时探索多个解,提高了搜索效率。此外,量子搜索的随机性也有助于避免算法陷入局部最优解。
(3)增强的搜索能力:与基本萤火虫算法相比,量子萤火虫算法通过引入量子计算的思想,使得萤火虫的搜索能力得到显著提升。在解决复杂优化问题时,量子萤火虫算法能够更快地找到最优解或近似最优解。
三、算法的数学表达
在量子萤火虫算法中,萤火虫的位置和状态通常用量子态来表示。每个萤火虫可以看作是一个量子个体,其每个量子位的状态用概率幅度表示。这些概率幅度通常用量子角形式进行编码,如
![[\alpha, \beta ]^{T}=[cos\theta , sin\theta ]^{T}](/image/aHR0cHM6Ly9sYXRleC5jc2RuLm5ldC9lcT8lNUIlNUNhbHBoYSUyQyUyMCU1Q2JldGElMjAlNUQlNUUlN0JUJTdEJTNEJTVCY29zJTVDdGhldGElMjAlMkMlMjBzaW4lNUN0aGV0YSUyMCU1RCU1RSU3QlQlN0Q%3D)
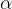
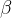
1.量子态的更新公式:
在量子萤火虫算法中,量子态的更新通常基于某种量子旋转门或量子变异操作。这些操作可以表示为矩阵乘法或向量运算的形式。具体的更新公式可能因算法的具体实现而异,但通常都包含量子旋转角度的计算和量子态的更新两个步骤。
(1)量子旋转角度的计算
在量子萤火虫算法中,每个萤火虫的位置通常用量子态来表示,而量子态的更新则依赖于量子旋转角度的计算。量子旋转角度通常是根据萤火虫之间的相对位置或亮度差异来确定的。具体来说,量子旋转角度θ可以通过某种函数关系与萤火虫之间的相对位置或亮度差异相关联。这个函数关系可能因算法的具体实现而异,但通常都包含一些基本的参数,如初始角度、衰减