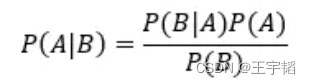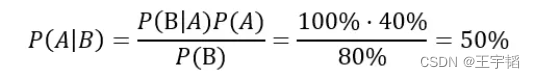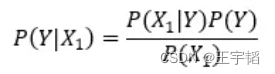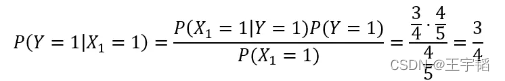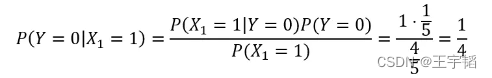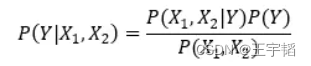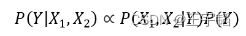朴素贝叶斯模型(了解)
这一章主要讲解机器学习中的朴素贝叶斯模型,包括朴素贝叶斯的算法原理和编程实现。同时将介绍一个朴素贝叶斯的经典案例:判断肿瘤为良性还是恶性来巩固所学知识点。
6.1 朴素贝叶斯模型算法原理
贝叶斯分类是机器学习中应用较为广泛的分类算法之一,其产生来自于贝叶斯对于逆概问题的思考,朴素贝叶斯是贝叶斯模型当中最简单的一种。
其算法核心为贝叶斯公式:
其中P(A)为事件A发生的概率,P(B)为事件B发生的概率,P(A|B)表示在事件B发生的条件下事件A发生的概率,同理P(B|A)则表示在事件A发生的条件下事件B发生的概率。
举个简单的例子,已知流感季节一个人感冒(事件A)的概率为40%(P(A)),一个人打喷嚏(事件B)的概率为80%(P(B)),一个人感冒的条件下打喷嚏的概率为100%(P(B|A)),那么已知一个人开始打喷嚏了,他是患感冒的概率为多少?这其实就是求这个人在打喷嚏的条件下患感冒的概率P(A|B),求解过程如下图所示:
6.1.1 一维特征向量下的贝叶斯模型
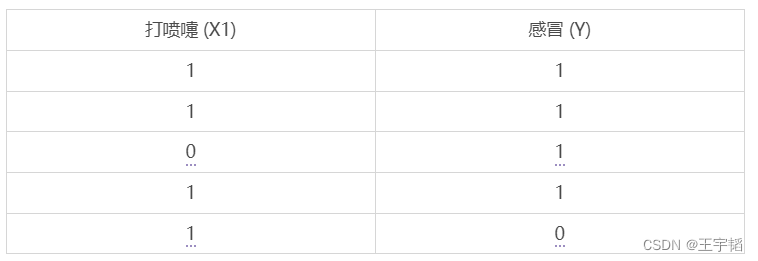
我们首先以一个更详细的例子来讲解一下贝叶斯公式更加偏实战的应用:如何判断一个人是否感冒了。假设已经有5个样本数据,如下表所示:
为方便演示,这里选取了一个特征变量:打喷嚏 (X1),其中数字1表示打喷嚏,0表示不打喷嚏;这里的目标变量是感冒 (Y),其中数字1表示感冒了,数字0表示未感冒。
根据上述数据,我们要利用贝叶斯公式,来预测一个人是否处于感冒的状态,比如说,一个人打喷嚏 (X1=1),那么他是否感冒了呢,也即预测他处于感冒状态的概率为多少,在数学上,我们把此概率写作P(Y|X1)。
应用贝叶斯公式有:
根据上述数据,我们可以计算在打喷嚏 (X1=1) 的条件下,患上感冒的概率为
其中P(X1=1|Y=1)为在已经感冒的条件下打喷嚏的概率,这里感冒的4个样本中打喷嚏的有3个,所以该概率为3/4;P(Y=1)则为所有样本中感冒的概率,这里5个人中有4个人感冒,所以为4/5;P(X1=1)则为所有样本中打喷嚏的概率,这里5个人中有4个人打喷嚏,所以为4/5。
同理在打喷嚏 (X1=1) 的条件下,没有患上感冒的概率为:
其中P(X1=1|Y=0)为在未感冒的条件下打喷嚏的概率,为1;P(Y=0)则为所有样本中未感冒的概率,为4/5;P(X1=1)则为所有样本中打喷嚏的概率,为4/5。
由于3/4大于1/4,所以在打喷嚏(X1=1) 的条件下患感冒的概率要高于不患感冒的概率,所以判断该人感冒了。
6.1.2 二维特征向量下的贝叶斯模型
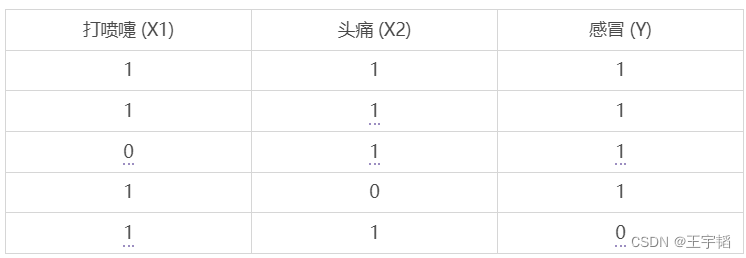
层层递进,我们加入另外一个特征变量:头痛(X2),其中数字1表示头痛,0表示不头痛;这里的目标变量仍为感冒(Y)。
根据上述数据,我们仍利用贝叶斯公式,来预测一个人是否处于感冒的状态,比如说,一个人他打喷嚏且头痛 (X1=1, X2=1) ,那么他是否感冒了呢,也即预测他处于感冒状态的概率为多少,在数学上,我们把此概率写作P(Y|X1,X2)。
应用贝叶斯公式有:
在比较 P(Y=1|X1,X2) 与 P(Y=0|X1,X2) 时,由于分母 P(X1,X2) 的值是相同的,所以我们在实际计算中可以舍去这部分的计算,直接比较两者分子大小即可。即:
补充知识点:独立性假设
在计算该概率之前,我们首先引入朴素贝叶斯模型的独立性假设:朴素贝叶斯模型中各特征之间相互独立,即