代码随想录day23｜二叉树结束｜669. 修剪二叉搜索树｜108.将有序数组转换为二叉搜索树｜538.把二叉搜索树转换为累加树｜Golang

代码随想录day23

事物是运动的时间是流逝的

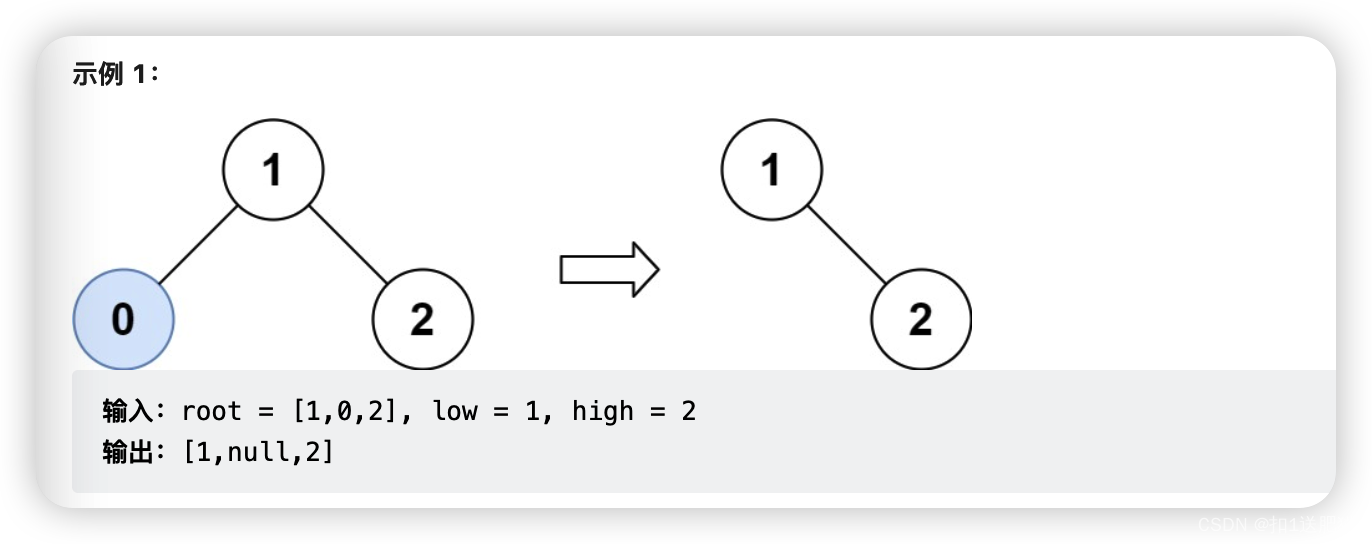
669. 修剪二叉搜索树

给定一个二叉搜索树，同时给定最小边界L 和最大边界 R。通过修剪二叉搜索树，使得所有节点的值在[L, R]中 (R>=L) 。你可能需要改变树的根节点，所以结果应当返回修剪好的二叉搜索树的新的根节点。

思路：

相信看到这道题目大家都感觉是一道简单题。但还真的不简单！

递归法：

直接想法就是：递归处理，然后遇到 root->val < low || root->val > high 的时候直接return NULL，一波修改，干净利落。然后就写出了下面的代码。

class Solution {
public:
    TreeNode* trimBST(TreeNode* root, int low, int high) {
        if (root == nullptr || root->val < low || root->val > high) return nullptr;
        root->left = trimBST(root->left, low, high);
        root->right = trimBST(root->right, low, high);
        return root;
    }
};

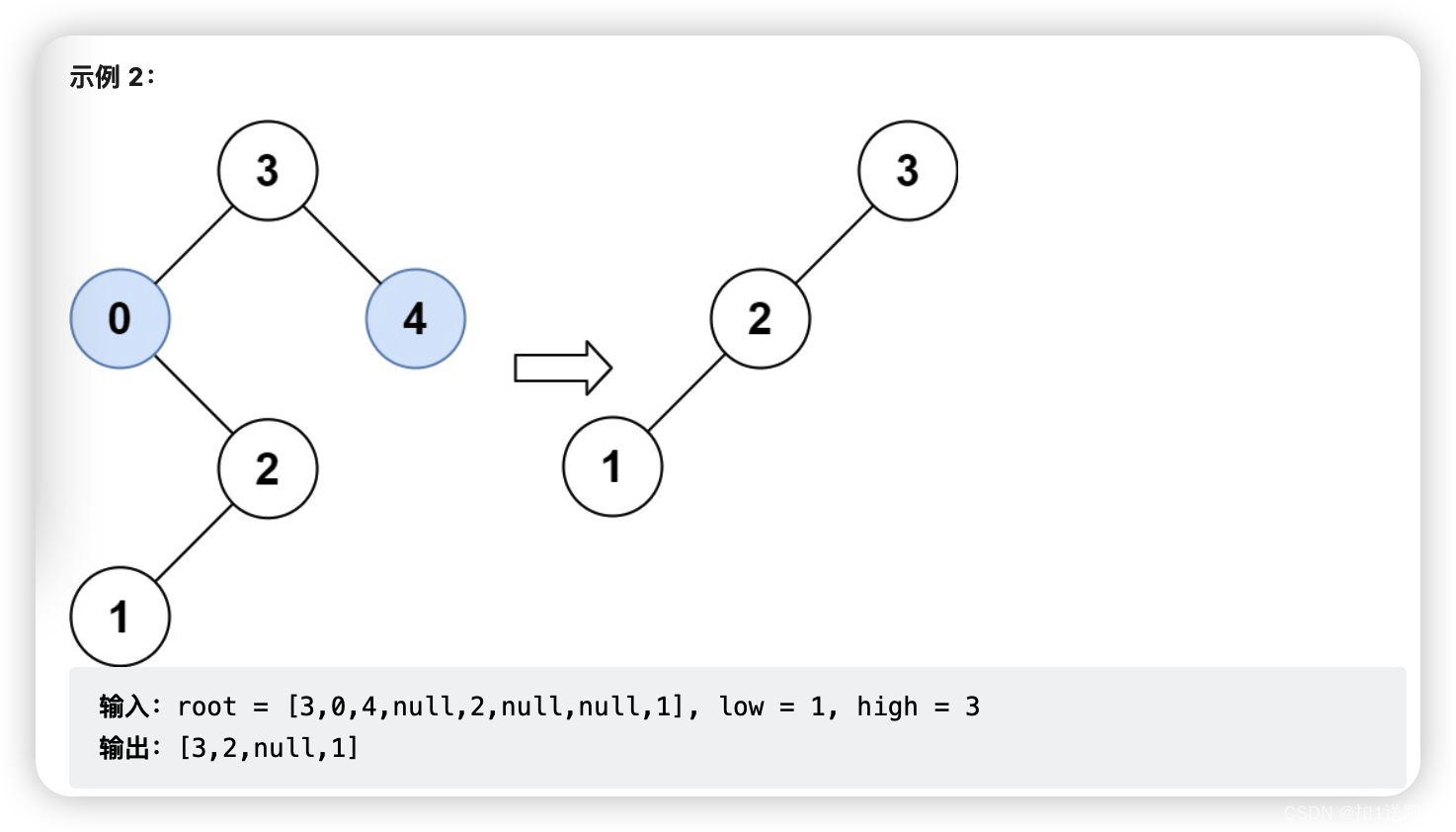
然而[1, 3]区间在二叉搜索树的中可不是单纯的节点3和左孩子节点0就决定的，还要考虑节点0的右子树。

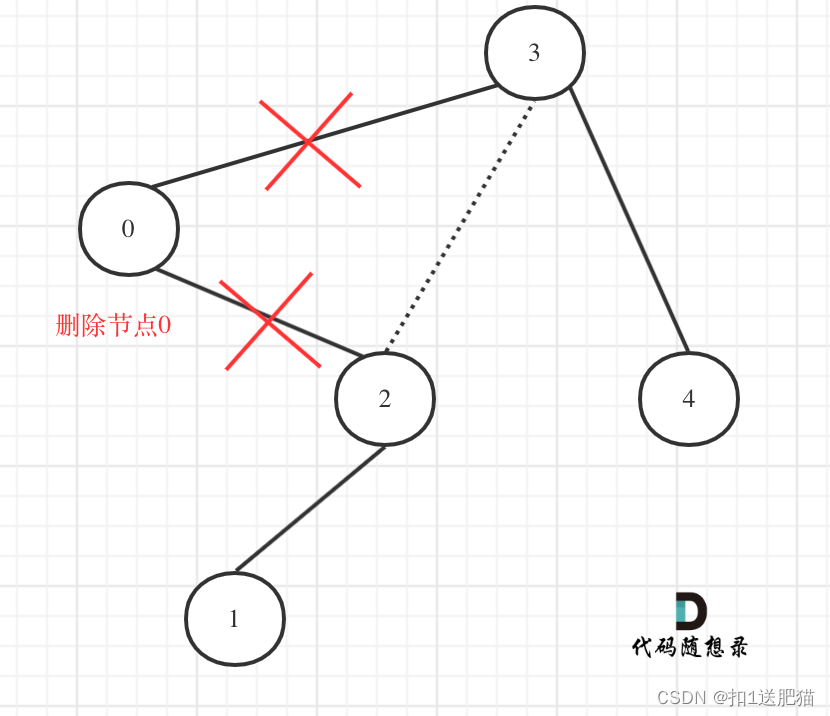
我们在重新关注一下第二个示例，如图：

所以以上的代码是不可行的！

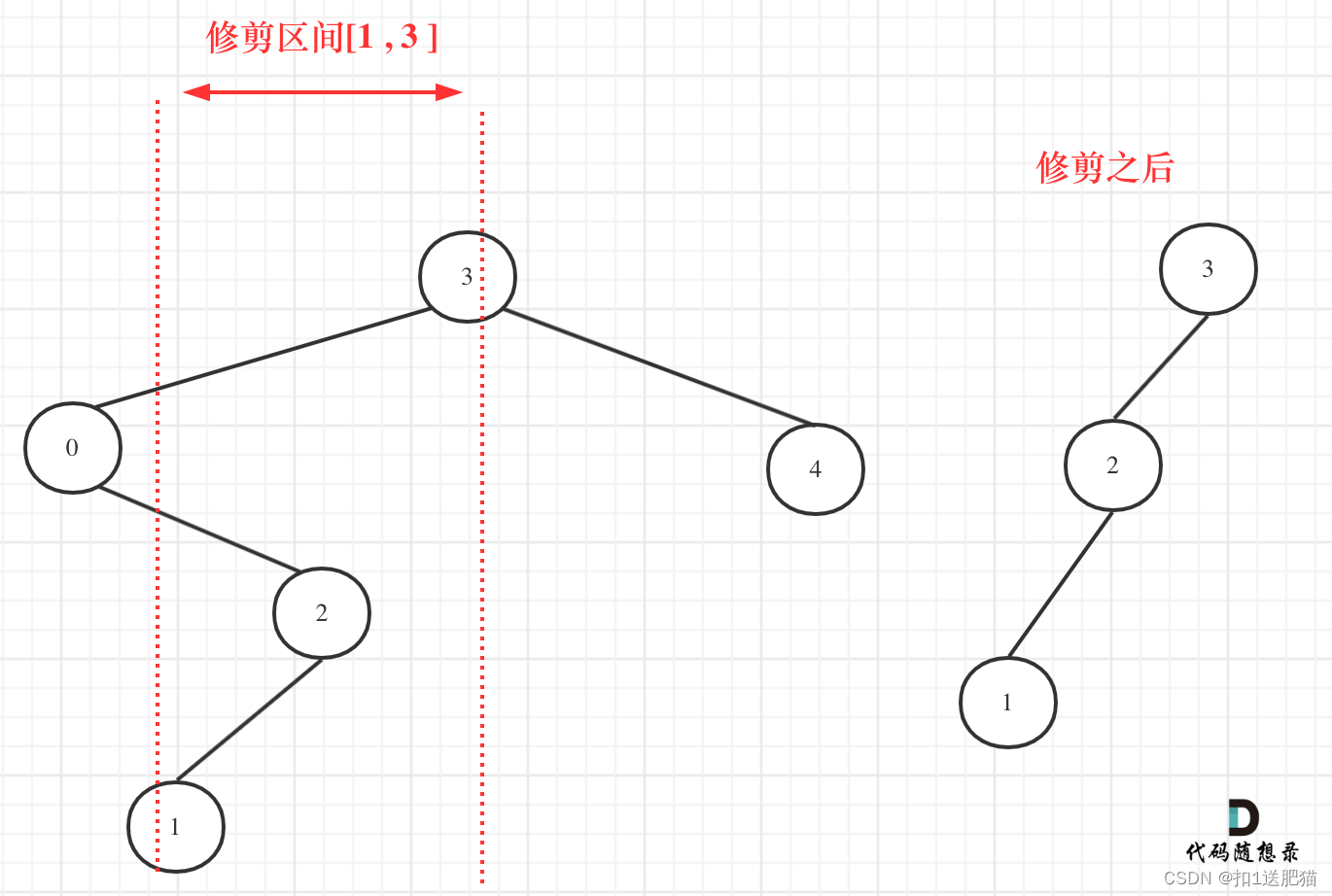
从图中可以看出需要重构二叉树，想想是不是本题就有点复杂了。其实不用重构那么复杂。

在上图中我们发现节点0并不符合区间要求，那么将节点0的右孩子节点2 直接赋给节点3的左孩子就可以了（就是把节点0从二叉树中移除），如图

理解了最关键部分了我们在递归三部曲：

1、确定递归函数的参数以及返回值：

这里我们为什么需要返回值呢？因为是要遍历整棵树，做修改，其实不需要返回值也可以，我们也可以完成修剪（其实就是从二叉树中移除节点）的操作。但是有返回值，更方便，可以通过递归函数的返回值来移除节点。

func trimBST(root *TreeNode, low int , high int ) *TreeNode{
}

2、确定终止条件：

修剪的操作并不是在终止条件上进行的，所以就是遇到空节点返回就可以了。

if root == nil {
    return nil
}

3、确定当前递归逻辑：

如果root（当前节点）的元素小于low的数值，那么应该递归右子树，并返回右子树符合条件的头结点。

    if root.Val<low{//如果该节点值小于最小值，则该节点更换为该节点的右节点值，继续遍历
        right:=trimBST(root.Right,low,high)
        return right
    }

如果root(当前节点)的元素大于high的，那么应该递归左子树，并返回左子树符合条件的头结点。

    if root.Val>high{//如果该节点的值大于最大值，则该节点更换为该节点的左节点值，继续遍历
        left:=trimBST(root.Left,low,high)
        return left
    }

接下来要将下一层处理完左子树的结果赋给root-.left，处理完右子树的结果赋给root-.right。

最后返回root节点，代码如下：

    root.Left=trimBST(root.Left,low,high)    // 更新     root.Left接住新的符合条件的节点啊
    root.Right=trimBST(root.Right,low,high)   // 更新    root.Right接住新的符合条件的节点啊
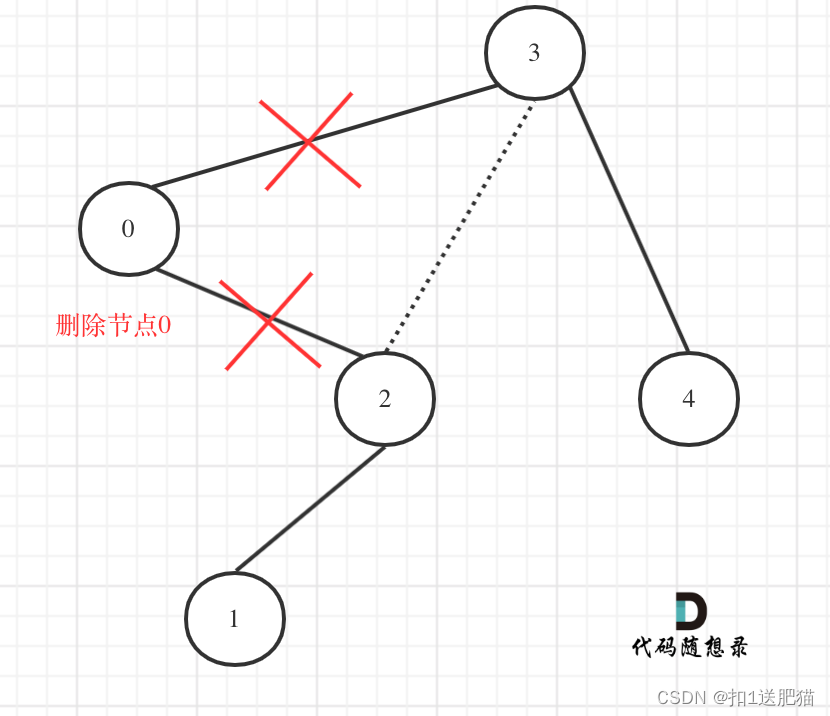
    return root

此时大家是不是还没发现这多余的节点究竟是如何从二叉树中移除的呢？再回顾一下上面的代码，针对下图中二叉树的情况：

如下代码相当于把节点0的右孩子（节点2）返回给上一层，

    if root.Val<low{//如果该节点值小于最小值，则该节点更换为该节点的右节点值，继续遍历
        right:=trimBST(root.Right,low,high)
        return right
    }

然后如下代码相当于用节点3的左孩子把下一层返回的节点0的右孩子（节点2）接住。

    root.Left=trimBST(root.Left,low,high)    // 更新     root.Left接住新的符合条件的节点啊

不难写出下面的Go代码

func trimBST(root *TreeNode, low int, high int) *TreeNode {
    if root==nil{
        return nil
    }
    if root.Val<low{//如果该节点值小于最小值，则该节点更换为该节点的右节点值，继续遍历
        right:=trimBST(root.Right,low,high)
        return right
    }
    if root.Val>high{//如果该节点的值大于最大值，则该节点更换为该节点的左节点值，继续遍历
        left:=trimBST(root.Left,low,high)
        return left
    }
    root.Left=trimBST(root.Left,low,high)    // 更新     root.Left接住新的符合条件的节点啊
    root.Right=trimBST(root.Right,low,high)   // 更新    root.Right接住新的符合条件的节点啊
    return root
}

108.将有序数组转换为二叉搜索树

思路：

做这道题目之前大家可以了解一下这几道：

106.从中序与后序遍历序列构造二叉树

654.最大二叉树中其实已经讲过了，如何根据数组构造一棵二叉树。

701.二叉搜索树中的插入操作

450.删除二叉搜索树中的节点

进入正题：

题目中说要转换为一棵高度平衡二叉搜索树。这和转换为一棵普通二叉搜索树有什么差别呢？

其实这里不用强调平衡二叉搜索树，数组构造二叉树，构成平衡树是自然而然的事情，因为大家默认都是从数组中间位置取值作为节点元素，一般不会随机取，所以想构成不平衡的二叉树是自找麻烦。

在二叉树：构造二叉树登场！和二叉树：构造一棵最大的二叉树中其实已经讲过了，如何根据数组构造一棵二叉树。

本质就是寻找分割点，分割点作为当前节点，然后递归左区间和右区间。

本题其实要比二叉树：构造二叉树登场！和二叉树：构造一棵最大的二叉树简单一些，因为有序数组构造二叉搜索树，寻找分割点就比较容易了。

分割点就是数组中间位置的节点。那么为问题来了，如果数组长度为偶数，中间节点有两个，取哪一个？取哪一个都可以，只不过构成了不同的平衡二叉搜索树。

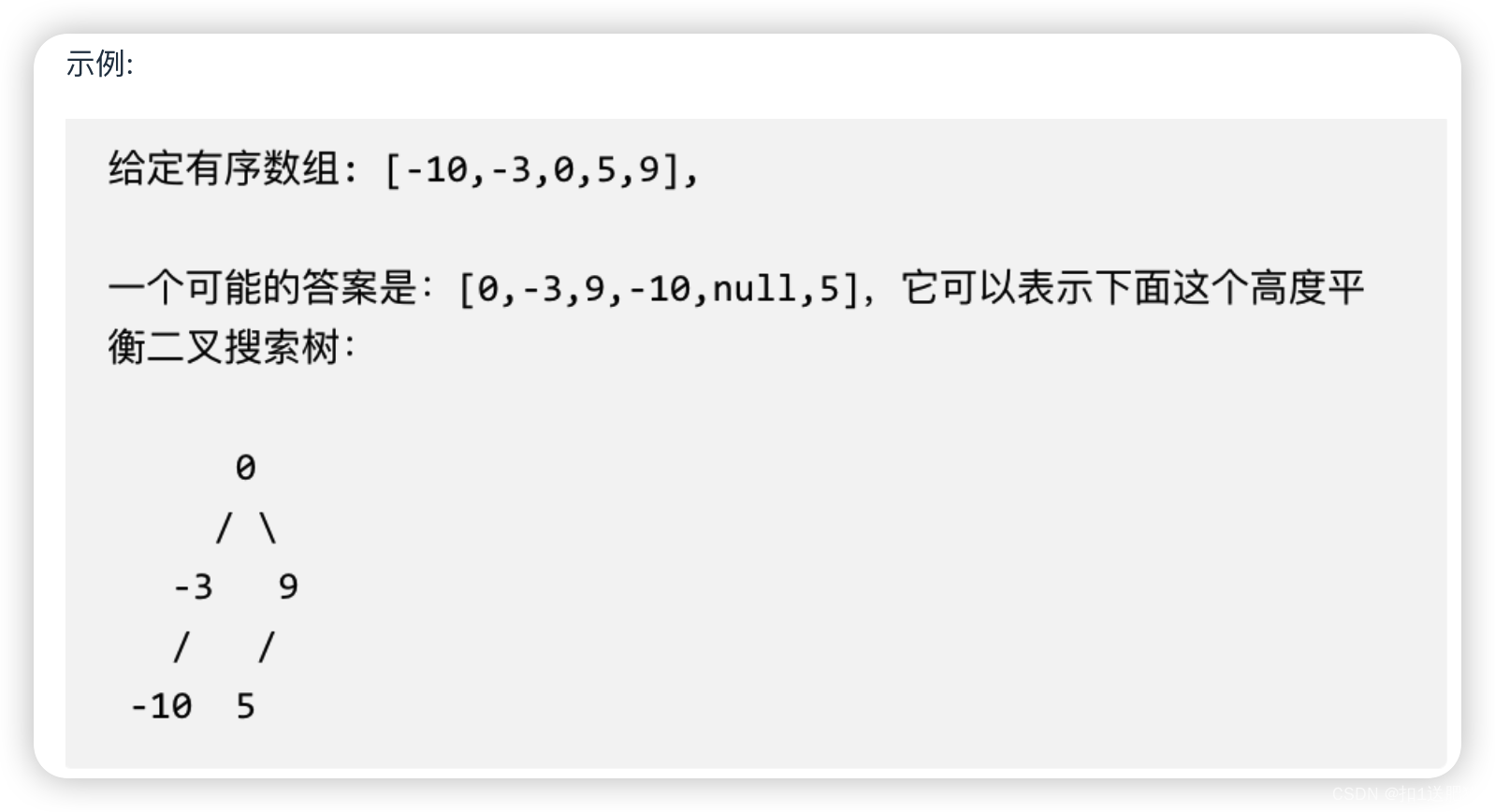
例如：输入：[-10,-3,0,5,9]

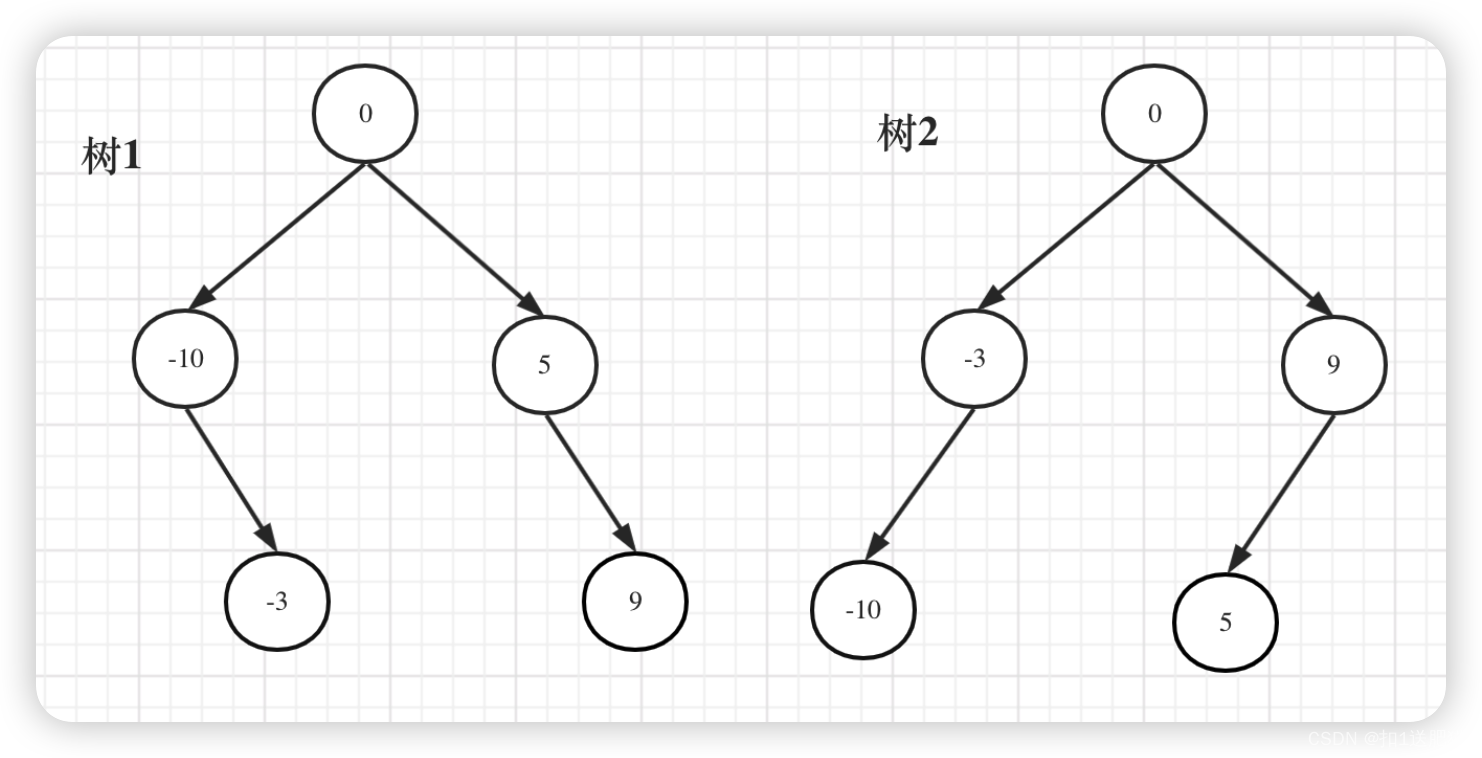
如下两棵树，都是这个数组的平衡二叉搜索树：

如果要分割的数组长度为偶数的时候，中间元素为两个，是取左边元素就是树1，取右边元素就是树2。这也是题目中强调答案不是唯一的原因。理解这一点，这道题目算是理解到位了。

递归：

1、确定递归函数返回值及其参数：

删除二叉树节点，增加二叉树节点，都是用递归函数的返回值来完成，这样是比较方便的。

相信大家如果仔细看了二叉树：搜索树中的插入操作和二叉树：搜索树中的删除操作，一定会对递归函数返回值的作用深有感触。那么本题要构造二叉树，依然用递归函数的返回值来构造中节点的左右孩子。

再来看参数，首先是传入数组，然后就是左下标left和右下标right。

我们在二叉树：构造二叉树登场！中提过，在构造二叉树的时候尽量不要重新定义左右区间数组，而是用下标来操作原数组。

// 左闭右闭区间[left, right]
func digui(nums []int, left, right int) *TreeNode{
}

这里注意，我这里定义的是左闭右闭区间，在不断分割的过程中，也会坚持左闭右闭的区间，这又涉及到我们讲过的循环不变量。

2、确定递归终止条件：

这里定义的是左闭右闭的区间，所以当区间 left > right的时候，就是空节点了。

if left > right {
    return nil
}

3、确定单层递归逻辑：

首先取数组中间元素的位置，不难写出 int mid = (left + right) / 2;，这么写其实有一个问题，就是数值越界，例如left和right都是最大int，这么操作就越界了，在二分法中尤其需要注意！

所以可以这么写：int mid = left + ((right - left) / 2); 但本题leetcode的测试数据并不会越界，所以怎么写都可以。但需要有这个意识！取了中间位置，就开始以中间位置的元素构造节点，代码：TreeNode* root = new TreeNode(nums[mid]);。

接着划分区间，root的左孩子接住下一层左区间的构造节点，右孩子接住下一层右区间构造的节点。最后返回root节点，单层递归整体代码如下：

mid := left + (right - left) / 2
root := &TreeNode{Val:nums[mid],
                  Left:nil,
                  Right:nil,
                  }
root.Left = digui(nums,left,mid-1)
root.Right = digui(nums, mid+1, right)
return root

这里mid := left + (right - left) / 2 的写法相当于是如果数组长度为偶数，中间位置有两个元素，取靠左边的。

递归整体代码如下：

func sortedArrayToBST(nums []int) *TreeNode {
    return traversal(nums, 0, len(nums)-1)
}
func traversal(nums []int, left int, right int) *TreeNode {
    if left > right {
        return nil
    }
    // 找到分割点
    mid := left + (right - left) / 2
    root := &TreeNode {
        Val : nums[mid],
        Left : nil,
        Right : nil,
    }
    // 递归左区间和右区间
    root.Left = traversal(nums, left, mid - 1)
    root.Right = traversal(nums, mid + 1, right)
    return root
}

注意：在调用traversal的时候为什么传入的left和right为什么是0和len(nums) - 1，因为定义的区间为左闭右闭

538、把二叉搜索树转换为累加树

思路：

一看到累加树，相信很多小伙伴都会疑惑：如何累加？遇到一个节点，然后在遍历其他节点累加？怎么一想这么麻烦呢。

然后再发现这是一棵二叉搜索树，二叉搜索树啊，这是有序的啊。那么有序的元素如果求累加呢？

其实这就是一棵树，大家可能看起来有点别扭，换一个角度来看，这就是一个有序数组[2, 5, 13]，求从后到前的累加数组，也就是[20, 18, 13]，是不是感觉这就简单了。

为什么变成数组就是感觉简单了呢？

因为数组大家都知道怎么遍历啊，从后向前，挨个累加就完事了，这换成了二叉搜索树，看起来就别扭了一些是不是。

那么知道如何遍历这个二叉树，也就迎刃而解了，从树中可以看出累加的顺序是右中左，所以我们需要反过来中序遍历这个二叉树，然后顺序累加就可以了

递归：

本题依然需要一个pre指针记录当前遍历节点cur的前一个节点，这样才方便做累加。

pre指针的使用技巧，我们在二叉树：搜索树的最小绝对差和二叉树：我的众数是多少？都提到了，这是常用的操作手段。

1、递归函数参数以及返回值：

这里很明确了，不需要递归函数的返回值做什么操作了，要遍历整棵树。同时需要定义一个全局变量pre，用来保存cur节点的前一个节点的数值，定义为int型就可以了。

var pre int
func digui(cur *TreeNode) *TreeNode{
}

2、确定终止条件：

if cur == nil {
    return 
}

3、确定单层递归逻辑：

注意要右中左来遍历二叉树，中节点的处理逻辑就是让cur的数值加上前一个节点的数值。

digui(cur.Right) // 右
cur.Val += pre
pre = cur.Val
digui(cur.Left)  // 左

递归法整体代码如下：

var pre int
func convertBST(root *TreeNode) *TreeNode {
    pre = 0 
    digui(root)
    return root
}
func digui(cur *TreeNode) *TreeNode{
    if cur == nil {    //终止条件，遇到空节点就返回
        return nil
    }
    digui(cur.Right)     //先遍历右边
    cur.Val += pre
    pre = cur.Val
    digui(cur.Left) //遍历左节点
    return cur
}

二叉树基础结束啦。